GCN - Semi-Supervised Classification with Graph Convolutional Networks 用图卷积进行半监督节点分类 ICLR 2017

论文：Semi-Supervised Classification with Graph Convolutional Networks
使用图卷积网络进行半监督节点分类

作者：Thomas N. Kipf, Peter Bloem, Rianne van den Berg, Ivan Titov, Max Welling
荷兰阿姆斯特丹大学

来源：ICLR 2017

论文链接：https://arxiv.org/abs/1609.02907

Github链接： https://github.com/tkipf/gcn

Abstract

本文提出了一种可扩展的基于图数据结构的半监督学习方法，该方法基于一个有效的卷积神经网络变形，这种变形能够直接对图进行操作（卷积层变为了图卷积层）。文中通过谱图卷积（spectral graph convolution）的局部一阶近似（localized first-order approximation） 来确定卷积网络结构的选择。图卷积的模型在图的边的数量上呈线性关系，并可以学习隐藏层表示，这些表示既编码局部图结构，也能够编码节点的特征。在大量关于引用网络和知识图谱网络数据集的实验后，作者认为他们的方法显著优于相关方法。

通过图结构数据中部分有标签的节点数据对卷积神经网络结构模型训练，使网络模型对其余无标签的数据进行进一步分类。

1.Intruduction

考虑对图（例如引文网络）中的节点（如引文网络中的文章）进行分类的问题，其中仅有一小部分节点有标签（即明确知道该节点属于哪一类）。这个问题可以被定义为基于图的半监督学习，(Zhu et al., 2003; Zhou et al., 2004; Belkin et al., 2006; Weston et al., 2012)等人在处理该问题时借助基于图的正则化形式将标签信息与图结构数据平滑的结合，其具体操作是在代价函数中加入图形化的拉普拉斯正则项如下式（1）所示：

$$\mathcal{L}={\mathcal{L}}_0+\lambda {\mathcal{L}}_{reg},with{L}_{reg}=\sum _{i,j}{A}_{i,j}||f(X_i)-f(X_j)|{|}^2=f(X{)}^T\Delta f(X)(1)$$

• ${\mathcal{L}}_0$表示图中有label部分的监督损失
• $f(\cdot )$是一个可微函数,为传播规则
• $\lambda$是一个加权因子
• $X$ 是节点特征向量 Xi的矩阵，即特征矩阵
• $A\in {\mathbb{R}}^{N\times N}$（权重为0，1或者加权）表示邻接矩阵
• $D_{ii}={\sum }_j{A}_{ij}$表示度矩阵
• $\Delta =D-A$ 表示无向图 G=(V,E)的非标准图拉普拉斯算子

式（1）的局限性在于它依赖于图中的相连节点有着相同标签这个假设。而实际情况下，图中的边可能并不一定能够反应出节点之间的相似性而可能是一些其他的信息，因此这个假设可能会限制模型的效果。

在本文中，作者直接使用神经网络模型$f(X,A)$对图结构进行编码，并对所有带标签的节点进行有监督 loss${\mathcal{L}}_0$ 训练，从而避免在损失函数中进行基于显示的图的正则化。在图的邻接矩阵上调节f(⋅) 将允许模型从监督损失${\mathcal{L}}_0$中分配梯度信息，并使其能够学习带标签用和不带标签的节点的表示。

本文做了两方面的工作。首先，对于直接操作于图结构数据的网络模型根据频谱图卷积(Hammond等人于2011年提出的Wavelets on graphs via spectral
graph theory)使用一阶近似简化计算的方法，提出了一种简单有效的层式传播方法。其次，验证了为什么可以将这种基于图形的神经网络模型可用于快速可扩展式的处理图数据中节点半监督分类问题。对许多数据集进行的研究表明，本文的模型在分类准确性和效率上与半监督学习的最新方法相比有优势（作者通过在一些公开数据集上验证了自己的方法的效率和准确率能够媲美现有的顶级半监督方法）。

小结：

• 使用神经网络模型 $f(X,A)$对所有带标签节点进行基于监督损失的训练。X为输入数据，A为图的邻接矩阵。$f()$或$f(x)$或$f(X,A)$都可以理解为传播规则。
• 在图的邻接矩阵上调整 $f()$将允许模型从监督损失 L0中分配梯度信息，并使其能够学习所有节点（带标签或不带标签）的表示。
• GSP（graph signal processing）图形信号处理，顾名思义就是将图当做信号，然后运用信号处理的方法去分析与处理Graph的特征。借助于图的拉普拉斯矩阵的特征值和特征向量来研究Graph的性质。
• 图的性质可以表示在拉普拉斯矩阵之中，即图的性质可以通过拉普拉斯矩阵体现出来。这样，对图的分析，可以变为对拉普拉斯矩阵的分析。

创新有两点：

• 对直接操作于图结构数据的网络模型根据频谱图卷积(Hammond等人于2011年提出的Wavelets on graphs via spectral graph theory)使用一阶近似简化计算的方法，提出了一种简单有效的层式传播方法。
• 验证了图结构神经网络模型可用于快速可扩展式的处理图数据中节点半监督分类问题，作者通过在一些公有数据集上验证了自己的方法的效率和准确率能够媲美现有的顶级半监督方法。

2.Fast Approximate Convolutions on Graphs（图的快速近似卷积）

每一个神经网络层可以写成$H^{l+1}=f(H^l,A)$,这个模型主要依赖于函数f和参数化的选择。在本节中，作者为特定的基于图的神经网络模型f(X,A)提供本文后面用到的理论机制，考虑具有以下分层传播规则的多层图形卷积网络（GCN）（即考虑一个简单的例子，这里的f取σ激活函数）：

$$H^{(l+1)}=f(H^l,A)=\sigma ({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}{H}^{(l)}{W}^{(l)})(2)$$

• A是图的邻接矩阵
• $\tilde{A}=A+I_N$是带有自环的无向图的邻接矩阵。
• $I_N$ 是单位矩阵。
• ${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$是带有自环的无向图的度矩阵，是一个对角矩阵。
• $W^{(l)}$ 是一个可训练权重矩阵或参数矩阵。
• σ(⋅) 激活函数，例如Relu。
• $H^{(l)}\in {\mathbb{R}}^{N\times D}$是第l层的激活矩阵,第l层的结点的特征（可以理解为第l-1层的输出）；$H^{(0)}=X$。
• 输入：结点特征X（N×D，其中N是节点数，D是输入的特征数），图的邻接矩阵A
• 输出：节点层面的矩Z（ N×F，F是每个节点的输出特征数）
• 乘矩阵A：对于每个节点，把除自身（除了有自循环外）外相邻节点的特征全加起来接下来

接下来，文中证明了这种传播规则的形式可以通过图上局域谱滤波器的一阶近似得到。(Hammond et al.(2011)和 Defferrard et al. 2016)。

下面介绍的谱图卷积其实就是Chebyshev谱CNN（ChebNet）。

2.1 Spectral Graph Convolutins（谱图卷积）

考虑信号$x\in {\mathbb{R}}^N$（x就是graph上对应于每个顶点的feathure vector，即由数据集提取特征构成的向量，而不是和线性代数中常说的特征向量，注意区别）与以参数为 $θ∈\mathbb{R}^N $的滤波器 $g_θ=diag(θ) $在傅里叶域的谱卷积。

$$g_{\theta }\ast x=U{g}_{\theta }{U}^{T}x(3)$$
其中

• U 是对称归一化的拉普拉斯(normalized graph Laplacian)算子$L=I_N-D^{-1/2}A{D}^{-1/2}=U\Lambda U^T$的特征向量矩阵，Λ是由L的特征向量构成的对角矩阵。

$$\begin{array}{rl}L& =D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}\\ & =D^{-\frac{1}{2}}D{D}^{-\frac{1}{2}}-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\\ & =I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\end{array}$$
由于normalized graph Laplacian矩阵L是实对称矩阵, 因此其特征向量矩阵U是正交矩阵,即$U{U}^T=I_N$

• $U^{T}x$是x的傅里叶变换。
• $g_{\theta }$是由参数θ构成的对角矩阵diag(θ)。由于参数θ的确定与L的特征值有关,作者认为$g_{\theta }$是特征值 Λ的一个函数，即令

$$g_{\theta }=g_{\theta }(\Lambda )$$

式3的计算量很大，因为特征向量矩阵U 的复杂度是$O(N^2)$。此外，对于大型图来说，L特征值分解的计算量也很大。
为了解决这个问题，Hammond et al.(2011) ：Wavelets on graphs via spectral graph theory指出$g_{\theta }(\Lambda )$可以很好的通过Chebyshev多项式$T_k(x)$ 的Kth-阶截断展开来拟合，并对Λ进行scale使其元素位于[−1,1]：

$$g_{\theta }(\Lambda )\approx \sum _{k=0}^K{\theta }_k{T}_K(\tilde{\Lambda })(4)$$
其中

• $\tilde{\Lambda }=2\Lambda /{\lambda }_{max}-I_N$(为缩放后的特征向量矩阵,缩放后范围是[−1,1]，单位矩阵的特征值是n重1)，缩放的目的是为了满足Chebyshev多项式$T_k(x)$ 的$K^{th}$ 阶截断展开的条件：自变量范围需要在[−1,1]之间
• ${\lambda }_{max}$是L 的最大特征值，也叫谱半径。
• $\theta \in {\mathbb{R}}^K$ 是切比雪夫系数的向量
• Chebyshev多项式递归定义为$T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x)$， 其中$T_0(x)=1，T_1(x)=x$ 。

回到对信号x与滤波器$g_{\theta }$的卷积的定义，现在有：

$$g_{\theta }\ast x=\sum _{k=0}^K{\theta }_k{T}_K(\tilde{L})x(5)$$
其中

• $\tilde{L}=2L/{\lambda }_{max}-I_N=U\tilde{\Lambda }{U}^T$
• 易证 $(U\Lambda U^T{)}^k=U{\Lambda }^k{U}^T$

注意，此表达式现在是K-localized，因为它是拉普拉斯算子中的Kth-阶多项式，即它仅取决于离中央节点(Kth阶邻域)最大K步的节点。式5的复杂度是O(|E|)，即与边数呈线性关系。Defferrard et al. 2016：Toward an Architecture for Never-Ending Language Learning使用这个K-localized卷积来定义图上的卷积神经网络。

---

公式4到公式5的补充证明如下：
（1）先用数学归纳法证明

$$U{T}_k(\tilde{\Lambda })U^T=T_k(U\tilde{\Lambda }{U}^T)$$
数学归纳法思路：当n=1时显然成立，假设n=k时成立，只需证n=k+1时成立

证明：
根据切比雪夫多项式的定义, 已知
$$\begin{array}{rl}& U{T}_0(\tilde{\Lambda })U^T=U{U}^T=1=T_0(U\tilde{\Lambda }{U}^T)\\ & U{T}_1(\tilde{\Lambda })U^T=U\tilde{\Lambda }{U}^T=T_1(U\tilde{\Lambda }{U}^T)\end{array}$$
假设对于任意k>1, 满足
$$U{T}_{k-2}(\tilde{\Lambda })U^T=T_{k-2}(U\tilde{\Lambda }{U}^T)$$
与

$$U{T}_{k-1}(\tilde{\Lambda })U^T=T_{k-1}(U\tilde{\Lambda }{U}^T)$$
则

$$\begin{array}{rl}U{T}_k(\tilde{\Lambda })U^T& =2U\tilde{\Lambda }{T}_{k-1}(\tilde{\Lambda })U^T-U{T}_{k-1}(\tilde{\Lambda })U^T\\ & =2(U\tilde{\Lambda }{U}^T)\left[U{T}_{k-1}(\tilde{\Lambda })U^T\right]-U{T}_{k-1}(\tilde{\Lambda })U^T\\ & =2(U\tilde{\Lambda }{U}^T)T_{k-1}(U\tilde{\Lambda }{U}^T)-T_{k-1}(U\tilde{\Lambda }{U}^T)\\ & =T_k(U\tilde{\Lambda }{U}^T)\end{array}$$
因此,根据数学归纳法, 证毕。

(2)已知

$$\tilde{L}=U\tilde{\Lambda }{U}^T$$

（3）将（1）、（2）两式带入卷积公式：

$$\begin{array}{rl}{g}_{\theta }\ast x& =U{g}_{\theta }{U}^{T}x\\ & =U{g}_{\theta }(\Lambda )U^{T}x\\ & =U(\sum _{k=0}^K{\theta }_k{T}_K(\tilde{\Lambda }))U^{T}x\\ & =(\sum _{k=0}^K{\theta }_k{T}_K(U\tilde{\Lambda }{U}^T))x\\ & =\sum _{k=0}^K{\theta }_k{T}_K(\tilde{L})x(5)\end{array}$$

---

2.2 Layer-wise Linear Model（逐层线性模型）

简化：K=1（2个参数的模型）

因此可以通过堆叠多个形式为式5的卷积层来建立基于图卷积的神经网络模型。现在，文中将分层卷积操作限制为K=1（式5），即关于L是线性的，因此在图拉普拉斯谱上具有线性函数。

(以上展示了改进后的卷积的形式，都是前人的工作，本文的工作如下)

在GCN的这个线性公式中，作者进一步近似${\lambda }_{max}\approx 2$ , 可以预测到GCN的参数能够在训练中适应这一变化。根据这些近似，式5简化为：

$$\begin{array}{rl}{g}_{\theta }\ast x& =\sum _{k=0}^K{\theta }_k{T}_K(\tilde{L})x\\ & =\sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(\frac{2}{{\lambda }_{max}}L-I_N)x\\ & =\sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(L-I_N)x（{\lambda }_{max}\approx 2）\\ & =\left[{\theta }_0^{{}^{\prime }}{T}_0(L-I_N)+{\theta }_1^{{}^{\prime }}{T}_1(L-I_N)\right]x\\ & ={\theta }_0^{{}^{\prime }}x+{\theta }_1^{{}^{\prime }}(L-I_N)x\\ & ={\theta }_0^{{}^{\prime }}x+{\theta }_1^{{}^{\prime }}(I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}-I_N)x(L=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}})\\ & ={\theta }_0^{{}^{\prime }}x-{\theta }_1^{{}^{\prime }}{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}x\end{array}$$

即
$$g_{{\theta }^{{}^{\prime }}}\ast x\approx {\theta }_0^{{}^{\prime }}x+{\theta }_1^{{}^{\prime }}(L-I_N)x={\theta }_0^{{}^{\prime }}x-{\theta }_1^{{}^{\prime }}{D}^{-1/2}A{D}^{-1/2}x(6)$$
有两个自由参数${\theta }_0^{{}^{\prime }}$和${\theta }_1^{{}^{\prime }}$。滤波器参数可以被整个图上共享。连续应用这种形式的滤波器，然后有效地卷积节点的kth-阶邻域，其中k是神经网络模型中连续滤波操作或卷积层的数目。

简化：1个参数的模型

实际上，进一步限制参数的数量以解决过拟合并最小化每层的操作数量（例如矩阵乘法）会是有益的。具体来说, 文中令$\theta ={\theta }_0^{{}^{\prime }}=-{\theta }_1^{{}^{\prime }}$(假设参数共享), 则有：

$$g_{\theta }\ast x\approx \theta (I_N+D^{-1/2}A{D}^{-1/2})x(7)$$
其中

• 而$I_N+D^{-1/2}A{D}^{-1/2}$是有范围[0,2]的特征值。因此，如果在深度神经网络模型中使用该算子，则反复应用该算子会导致数值不稳定（发散）和梯度爆炸/消失。

为了解决该问题, 引入了一个renormalization trick（归一化技巧）：

$$I_N+D^{-1/2}A{D}^{-1/2}\stackrel{\tilde{A}=A+I_N}{⟶}{\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}$$
其中

• $\tilde{A}=A+I_N,{\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$，即图中加上自环

再加上一个激活函数，最后就可以得到公式（2）的快速卷积公式了：
$$H^{(l+1)}=f(H^l,A)=\sigma ({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}{H}^{(l)}{W}^{(l)})(2)$$

• $W$就是参数$\theta$参数矩阵

推广：特征映射公式

可以将这个定义推广到具有C个输入通道（即每个节点的C维特征向量）的信号$X\in {\mathbb{R}}^{N\times C}$和 F 个滤波器或特征映射如下：

$$Z={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}X\Theta (8)$$
其中

• $\Theta \in {\mathbb{R}}^{C\times F}$ 是一个滤波器参数矩阵
• $Z\in {\mathbb{R}}^{N\times F}$ 是卷积信号参数矩阵。

这个滤波操作复杂度是 $O(|E|FC)$，因为$\tilde{A}X$可以有效地实现为密集矩阵和稀疏矩阵的乘积。（在源代码中使用了稀疏矩阵和稠密矩阵乘法）

3. Semi-supervised Node Classfication（半监督节点分类）

前面介绍了一个简单灵活的可以在图上有效地传播信息模型$f(X,A)$ ，现重新回到半监督节点分类的问题上。

如前言所述，可以通过调整作者的模型$f(X,A)$来放松通常在基于图的半监督学习中所做的某些假设，此文希望这种设置可以在邻接矩阵种包含信息但数据$X$没有表现出来的情况下更有用($X$没有特征，通常输入单位矩阵)，例如引用网络中文档之间的引用链接或知识图谱中的关系。整体半监督学习的多层GCN模型，如图1所示。

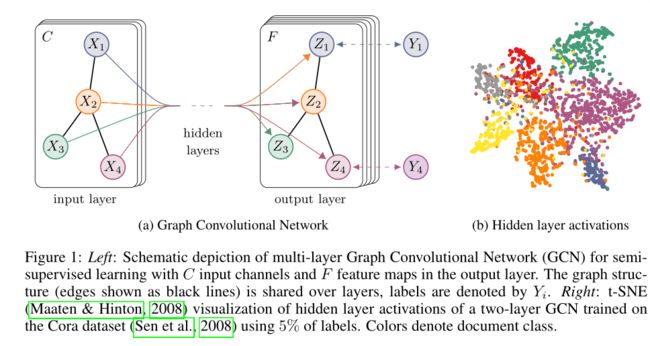
上图中，左(a)是一个GCN网络示意图，在输入层拥有CC个输入，中间有若干隐藏层，在输出层有$F$个特征映射；图的结构（边用黑线表示）在层之间共享；标签用$Y_i$表示。
右图(b)是一个两层GCN在Cora数据集上（使用了5%的标签）训练得到的隐藏层激活值的形象化表示，颜色表示文档类别。

3.1 Example（例子）

接下来，考虑一个两层的半监督节点分类GCN模型，在对称邻接矩阵A(binary or weighted) 上操作。

预处理操作

在预处理步骤中，首先计算
$$\hat{A}={\tilde{D}}^{-1/2}A{\tilde{D}}^{-1/2}$$
因此，前向计算变成一个简单的形式：

$$Z=f(X,A)=softmax(\hat{A}ReLU(\hat{A}X{W}^{(0)})W^{(1)})(9)$$

• $W^{(0)}\in {\mathbb{R}}^{C\times H}$是输入层到隐藏层的权重矩阵，隐藏层有H个特征。
• $W^{(1)}\in {\mathbb{R}}^{H\times F}$是隐藏层到输出层的权重矩阵。
• softmax定义为 $softmax(x_i)=\frac{1}{Z}\exp (x_i),Z={\sum }_i\exp (x_i)$，softmax作用在每一行上

交叉熵误差

对于半监督多类别分类，评估所有标记标签的交叉熵误差：

$$\mathcal{L}=-\sum _{l\in y_L}\sum _{f=1}^F{Y}_{lf}ln{Z}_{lf}(10)$$
其中，$y_L$为带标签的节点集。

训练

神经网络的权重$W^{(0)}，W^{(1)}$通过梯度下降来进行训练。
使用完整的数据集对每个训练迭代执行批量梯度下降（ batch gradient descent）。只要数据集适合内存，这就是一个可行的选择。
邻接矩阵A使用稀疏表示法，内存需求是O(E)，E为边数，即和边数呈线性关系。
通过Dropout引入训练过程中的随机性（srivastava等人，2014）。
将内存效率扩展与小批随机梯度下降（mini-batch stochastic
gradient descent） 留作以后的工作。

3.2 Implementation（实现）

在实践中，利用TensorFlow，使用稀疏-密集矩阵乘法在GPU上高效实现了公式(9)。
$$Z=f(X,A)=softmax(\hat{A}ReLU(\hat{A}X{W}^{(0)})W^{(1)})(9)$$
计算式9的计算复杂度为$O（|E|CHF）$，即图边数的线性。

4. Related Work（相关工作）

本文的模型从基于图的半监督学习领域和最近对基于图的神经网络的研究中得到了启发。在下面的内容中文中者简要概述了这两个领域的相关工作。

4.1 Graph-based Semi-supervised Learning（基于图的半监督学习）

近年来提出了大量的基于图形表示的半监督学习方法，其中大部分方法分为两大类：使用某种形式的图拉普拉斯正则化和基于图嵌入的方法。 图形拉普拉斯正则化的显著例子包括标签传播（Zhu et al., 2003）、manifold
regularization (Belkin et al., 2006)和deep semi-supervised embedding (Weston et al., 2012)。

最近，人们的注意力转移到了学习graph embeddings 方法的模型上，这些方法受到了 skip-gram模型的启发（Mikolov et al., 2013年）。DeepWalk（Perozzi et al., 2014）通过在图上随机游走地采样来预测节点的局部邻域来学习embedding。LINE (Tang et al., 2015) and node2vec (Grover & Leskovec, 2016)使用更复杂的随机游走或BFS模式扩展了DeepWalk。然而，对于所有这些方法，需要一个multi-step pipeline，包括随机游走生成和半监督训练，其中每个步骤必须单独优化。Plantoid（Yang et al., 2016）通过在学习embedding过程中注入标签信息来缓解这种情况。

4.2 Neural NetWorks on Graph（图神经网络）

在Gori等人的研究中，已经引入了对图形进行操作的神经网络（2005年）；Scarselli等人（2009）提出一种循环神经网络。他们的框架要求重复应用压缩映射（contraction map）作为传播函数，直到节点表示达到稳定的固定点。这一限制后来被Li等人（2016）得到了缓解。他们提出在原有的图形神经网络框架中引入了现代的神经网络训练实践。Duvenaud等人（2015）引入类似于卷积的传播规则和针对graph-level分类的方法。他们的方法要求学习特定节点的度的权重矩阵，这些权重矩阵不适用于具有很多节点的度分布的大型图。相反，此文的模型每层使用一个权重矩阵，通过适当的邻接矩阵normalization处理不同的节点的度（见第3.1节）。

Atwood & Towsley（2016）最近推出了一种基于图的神经网络的节点分类相关方法。它们认为复杂度为$O(n^2)$，限制了可能的应用范围。在另一个相关的模型中，Niepert等人（2016）将图局部转换为序列，这些序列被送入传统的一维卷积神经网络，这需要在预处理步骤中定义节点顺序。

此文的方法是基于谱图卷积神经网络，由Bruna等人提出（2014年），后来由Deffarrard等人进行了扩展（2016），具有快速局部化卷积。与这些工作相比，作者在这里考虑的是大规模网络中的节点分类任务。实验表明，在这种情况下，可以对Bruna等人的原始框架进行一些简化（见第2.2节）（2014）和Deffrard等人（2016）提高了大规模网络的可扩展性和分类性能。

5. Experiments（实验）

本文通过下列实验对模型进行测试：

• 半监督文本分类-引文网络
• 半监督实体分类-知识图谱中提取的二部图
• 多种图传播模型评估
• 随机图运行时间分析

5.1 Datasets（数据集）

Citation networks

本文考虑三个引文网络数据集：Citeseer、Cora和PubMed（Sen等人，2008）。数据集包含每个文档的稀疏bag-of-words特征向量和文档之间的引用链接列表。本文将引用链接视为（无向）边，并构造一个二元对称邻接矩阵A。每个文档都有一个类标签。在训练时，每个类只使用20个标签。

NELL

NELL是从中引入的知识图中提取的数据集（Carlson，2010年）。知识图是一组与有向标记边（关系）相连的实体。实验中遵循Yang等人所述的预处理方案（2016年）。文中为每个实体对（E1，R，E2）分配单独的关系节点R1和R2作为（E1，R1）和（E2，R2）。其中，实体节点由稀疏特征向量描述。通过为每个关系节点分配一个唯一的one-hot表示来扩展NELL中的特征数量，从而有效地为每个节点生成61278维稀疏特征向量。这里的半监督任务只考虑训练集中每个类一个标记示例的极端情况。如果节点i和j之间存在一条或多条边，作者通过设置$A_{ij}=1$，从图中构造一个二元对称邻接矩阵（binary, symmetric adjacency matrix）。

Random graphs

文中模拟各种大小的随机图数据集进行实验，测量每个epoch的训练时间。对于一个具有n个节点的数据集，创建一个随机图，随机均匀地分配2n条边。将单位矩阵$I_N$作为输入特征矩阵x，从而隐式地采用一种无特征的方法，其中模型只知道每个节点的标识，由唯一的one-hot向量指定。文中为每个节点添加dummy标签$y_i=1$。

5.2 Experimental set-up（实验设置）

实验部分按照第3.1节的描述训练两层GCN，并评估1000个标记示例的测试集的预测精度。在附录B中提供了使用最多10层的更深层次模型的额外实验。文中按照Yang等人的方法选择相同的数据集（2016），并采用额外的500个标记超参数优化示例验证集（所有层的dropout rate、第一个GCN层的L2正则化因子和隐藏单元数量）。文中没使用验证集标签进行训练。

引文网络数据集

• 最大200迭代期
• Adam算法
• 学习率为0.01
• 停止条件：验证集loss连续十个迭代期没有下降
• 权重初始化方法：Xavier Glorot and Yoshua Bengio. Understanding the difficulty of training deep feedforward neural networks. In AISTATS, volume 9, pp. 249–256, 2010.
  -（按行）对输入特征向量归一化

随机图数据集

• 隐藏层32个单元
• 省略dropout和L2正则化

5.3 Baselines(基准模型)

比较了与Yang等人相同的基线模型（2016年）；

• label propagation(LP)
• semi-supervised embedding(SemiEmb)
• manifold regularization(ManiReg)
• DeepWalk
• iterative classification algorithm(ICA)
• Planetoid

一些对比：

• 进一步比较了Lu &Getoor（2003）提出的迭代分类算法（ICA），并结合两个逻辑回归分类器，一个单独用于局部节点特征，另一个用于使用局部特征和聚集运算符的关系分类。
• 首先，使用所有标记的训练集节点训练局部分类器，并使用它为关系分类器训练引导未标记节点的类标签。
• 在所有未标记的节点（使用本地分类器引导）上运行10次迭代（关系分类器）的随机节点排序迭代分类（relational classifier）。
• 二级正则化参数与聚合算子（count与prop，seesenetal.（2008））根据每个数据集的验证集性能分别选择。
• 最后，将其与Planetoid（Yang等人，2016）进行比较，总是选择其最佳性能的模型变体（转导型与感应型）作为基准。

6. Results（结果）

6.1 Semi-supervised Node Classfication （半监督节点分类）

结果汇总在表2中。表中数字以百分比表示分类准确度。对于ICA，计算了100次随机节点排序运行的平均精度。所有其他基线方法的结果均取自论文（Yang等人，2016）。Planetoid*表示在其论文中提出的变体之外的各自数据集的最佳模型。

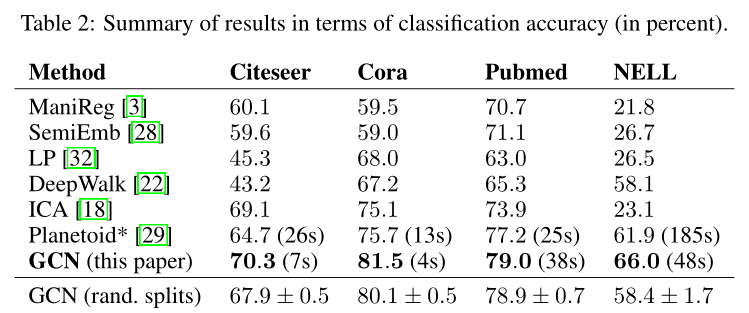
6.2 Evaluation of Propagation Model（传播模型的评价）

文中比较了在引文网络数据集上提出的每层传播模型的不同变体并按照前一节中描述的实验设置进行操作。结果汇总在表3中。作者最初的GCN模型的传播模型用renormalization
trick（粗体）表示。在所有其他情况下，两个神经网络层的传播模型都将替换为传播模型下指定的模型。表中数字表示100次随机权重矩阵初始化重复运行的平均分类精度。在每层有多个变量的情况下，文中对第一层的所有权重矩阵施加L2正则化。

6.3 Training Time Per Epoch (训练时间)

文中使用了100个epochs在模拟的随机图上每一个epoch的平均训练时间（前向传播、交叉熵计算、后向传播）的结果，以wall-clock时间测量。有关这些实验中使用的随机图数据集的详细描述，可参见第5.1节。文中比较了TensorFlow中GPU和Abadi等人仅CPU实现的结果（2015）。

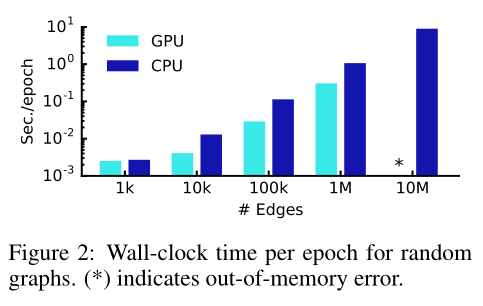
• Wall-clock time：就是响应时间，指计算机完成某一个任务所花的全部时间，也叫墙上时间（wall clock）或流逝时间(elapsed time)。

7. Discusion（讨论）

7.1 Semi-supervised Model（半监督模型）

本文提出的半监督节点分类输出器的方法在很大程度上形成了最新的相关方法。基于图拉普拉斯正则化的方法（Zhu et al.，2003；Belkin et al.，2006；Weston et al.，2012）最有可能受到限制，因为它们假设边缘编码节点的相似性。另一方面，Skip-gram由于其基于一条难以优化的multi-step pipeline而受到限制。本文提出的模型可以克服这两个限制，同时在效率（以wall clock时间测量）方面仍优于相关方法。与ICA（Lu & Getoor，2003）等仅聚合标签信息的方法相比，从每层相邻节点特征信息的传播提高了分类性能。

文中进一步证明，与简单的一阶模型（公式6）或使用切比雪夫多项式的高阶图卷积模型（式5）相比，所提出的传播模型（公式8）既提高了效率（减少了参数和运算，如乘法或加法），也提高了对许多数据集的预测性能。

高阶模型
$$g_{\theta }\ast x=\sum _{k=0}^K{\theta }_k{T}_K(\tilde{L})x(5)$$

一阶模型
$$g_{{\theta }^{{}^{\prime }}}\ast x\approx {\theta }_0^{{}^{\prime }}x+{\theta }_1^{{}^{\prime }}(L-I_N)x={\theta }_0^{{}^{\prime }}x-{\theta }_1^{{}^{\prime }}{D}^{-1/2}A{D}^{-1/2}x(6)$$

$$Z={\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}X\Theta (8)$$

7.2 Limitations and future work（限制和未来工作）

在这里，文中描述了当前模型的几个局限性，并概述了如何在未来的工作中克服这些局限性。

Memory requirement（内存要求）

在当前setup中，采用批量梯度下降（full-batch gradient descent），内存需求在数据集的大小上呈线性增长。文中已经证明，对于不适合GPU内存的大型图形，采用CPU训练仍然是一个可行的选择。小批量随机梯度下降（Mini-batch stochastic gradient descent）可以缓解这一问题。然而，生成Mini-batch的过程应该考虑到GCN模型中的层数，因为具有k层的GCN的k阶邻居必须存储在内存中，以便进行精确的过程。对于非常大且紧密相连的图数据集，可能需要进一步的近似。

Directed edges and edge features

文中的框架目前不支持边的特征（edge features）（即有向还是无向），只限于无向图（加权或不加权）。然而，NELL上的结果表明，通过将原始有向图表示为无向二部图，以及表示原始图中边缘的附加节点，可以处理有向边和边缘特征（详细信息见第5.1节）。

Limiting assumptions

通过第2节中介绍的近似，文中隐式地假定局部性（依赖于k层的gcn的k阶邻域）和自连接对相邻节点边的重要性相等。但是，对于某些数据集，在A的定义中引入一个权衡参数λ可能是有益的：

$$\tilde{A}=A+\lambda I_N(11)$$
在典型的半监督设置中，该参数现在扮演着与监督和非监督损失之间的权衡参数类似的角色（见等式1）。然而，在这里，它可以通过梯度下降来学习。

8. Conclusion（结论）

本文提出了一种新的图结构数据半监督分类方法，所提出的GCN模型使用了一种基于图上谱卷积的一阶近似的高效层传播规则。对多个网络数据集的实验表明，所提出的GCN模型能够以一种对半监督分类有用的方式对图结构和节点特征进行编码。在这种情况下，文中的模型在很大程度上优于最近提出的几种方法，同时具有不错的计算效率。

本文提出了一种图卷积神经网络，该网络可以被有效地用于处理图结构的数据。图卷积神经网络具有几个特点：

• 局部特性：图卷积神经网络关注的是图中以某节点为中心，K阶邻居之内的信息，这一点与GNN有本质的区别；
• 一阶特性：经过多种近似之后，GCN变成了一个一阶模型。也就是说，单层的GCN可以被用于处理图中一阶邻居上的信息；若要处理K阶邻居，可以采用多层GCN来实现；
• 参数共享：对于每个节点，其上的滤波器参数 W 是共享的，这也是其被称作图卷积网络的原因之一。

9.附录

Relation to Weisfeiler-Lehman (WL-1) Algorithm

图结构数据的神经网络模型最好能够学习图中节点的表示，同时考虑节点的图结构和特征描述。1-dim Weisfeiler-Lehman (WL-1)算法(Weisfeiler & Lehmann, 1968)提供了一个经过深入研究的框架，用于给定图和(可选的)离散初始节点标签的唯一分配。

其中

• $h_i^{(t)}$定义为节点$v_i$在第$t$次迭代的coloring（标签分配）
• ${\mathcal{N}}_i$表示节点$v_i$的邻居集合的索引
• $hash(\cdot )$是哈希函数
• 关于WL-1算法的深入数学讨论见，例如Douglas(2011)。

可以将算法1中的哈希函数替换为具有可训练参数的神经网络层状可微函数:

$$h_i^{(l+1)}=\sigma (\sum _{j\in {\mathcal{N}}_i}\frac{1}{c_{ij}}{h}_j^{(l)}{W}^{(l)})(12)$$
其中

• $c_{ij}$是边$(v_i,v_j)$的一个归一化常量
• $W^{(l)}$是第$l$层的参数矩阵
• $\sigma (\cdot )$是一个可微的非线性激活函数
• $h_i^{(l)}$是节点$i$在第$l$层网络的激活向量

通过选择$c_{ij}=\sqrt{d_i{d}_j}$（$d_i=|{\mathcal{N}}_i|$，定义为节点$v_i$的度），可以更新GCN的传播公式（2）为（12）。

$$H^{(l+1)}=f(H^l,A)=\sigma ({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}{H}^{(l)}{W}^{(l)})(2)$$

粗略地说，可以将GCN模型解释为图上1-dim Weisfeiler-Lehman (WL-1)算法的可微参数化泛化。

Node Embeddings with Random Weights

通过与Weisfeiler-Lehman算法的类比，可以发现，即使是一个未经训练的随机权重GCN模型，也可以作为一个强大的特征提取器来提取图中的节点。以3层GCN模型为例:

$$Z=tanh(\hat{A}tanh(\hat{A}tanh(\hat{A}X{W}^{(0)})W^{(1)})W^{(2)})(13)$$

• $W^{(l)}$是用Glorot & Bengio(2010)随机初始化的第$l$层的参数矩阵

文中将该模型应用于Zachary的空手道俱乐部网络(Zachary, 1977)。此图包含34个节点，由154条(无向和未加权的)边连接。每个节点都由四个类中的一个标记，通过基于模块的聚类得到(Brandes et al.， 2008)。如图3a所示。

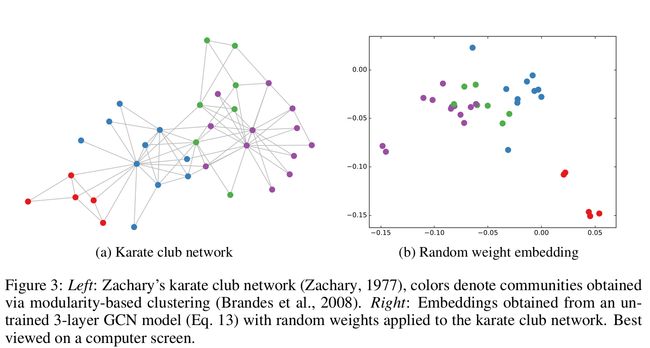
• 左图：Zachary的空手道俱乐部网络图，每个颜色表示一个聚类
• 有图：由公式（13）构成的3层GCN得到的Embeddings

实验设置

• 此实验中采用的是使用单位矩阵$I_N$代替特征矩阵$X$
• 节点无序
• 隐含层是4维（最初是2，单发现维数为4时，tanh(·)单元的饱和频率较低），最后输出是2维的，因此便于在图上显示

图3b显示了一个应用于空手道俱乐部网络的未训练的GCN模型得到的节点嵌入(输出Z)的典型示例。这些结果可与DeepWalk (Perozzi et al.， 2014)的embeddings进行比较，DeepWalk使用了代价更高的无监督训练过程。

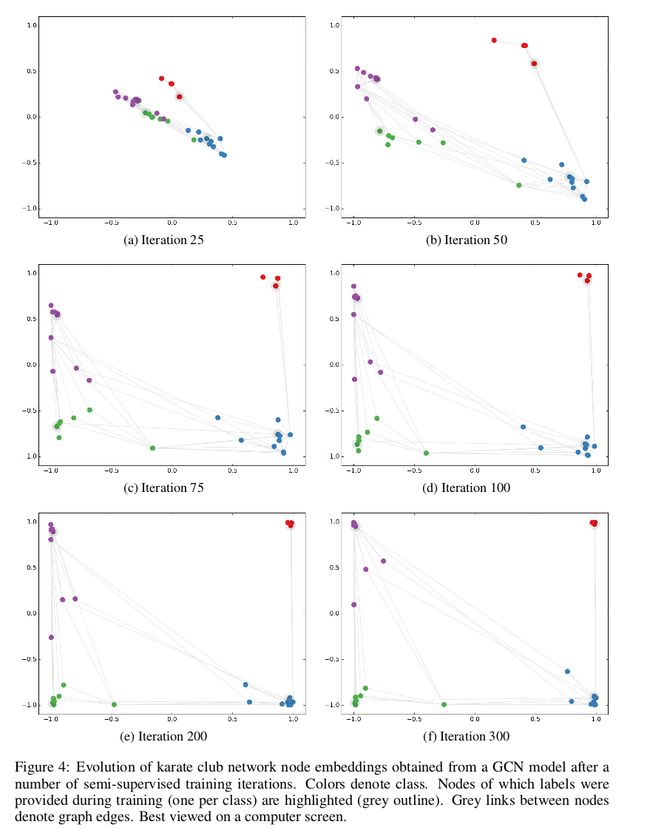
Semi-supervised Node Embeddings

在这个简单的GCN应用于空手道俱乐部网络的例子中，观察embeddings在训练半监督分类任务时的反应是很有趣的。这种可视化(参见图4)提供了关于GCN模型如何利用图结构(以及从图结构中提取后面的层的特征)来学习embeddings的深入的理解，这对分类任务有用的。

考虑以下半监督学习设置

• 在公式（13）基础上添加一个softmax层
• 每个类只使用一个带标记的示例进行训练(即总共有4个带标记的节点)
• 使用Adam (Kingma & Ba, 2015)对300个训练迭代进行训练
• 交叉熵损失的学习率为0.01。

图4显示了节点嵌入在许多训练迭代中的演化。该模型成功地实现了基于最小监督和图结构的社区线性分离。整个训练过程的视频可以在作者的网站上找到：http://tkipf.github.io/graph-convolutional-networks/

Experiments on Model Depth（残差连接）

文中还考虑了模型深度，也就是卷积层层数对分类性能的影响。实验中对Cora, Citeseer和Pubmed数据集的所有的标签使用吴冲交叉验证。除了公式2的标准GCN模型以外，文中还进行了一个模型的变种的实验：残差连接。隐含层之间使用残差连接，可以使模型能够传递来自前一层输入的信息，从而促进更深层次模型的训练。

$$H^{(l+1)}=\sigma ({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}{H}^{(l)}{W}^{(l)})+H^{(l)}(14)$$

实验设置

• 训练400个epochs
• 使用Adam优化器
• 学习率0.001
• 第一层和最后一层dropout率为0.5
• 第一层，L2正则化，$5\cdot 10^{-4}$
• 每个隐含层units数：16

对于上述数据集，仅使用2层或3层模型可获得最佳结果。实验可以观察到，对于深度超过7层的模型，不使用残差连接的训练会变得非常困难。两个原因：

• 每个节点的有效的context size随着其K阶邻域的大小的增加而增加
• 过度拟合可能成为一个问题，因为参数的数量随着模型深度的增加而增加。

10.补充（Graph classification）

此文的github表明，此框架还支持使用每个邻接矩阵对多个图实例(大小可能不同)进行批量分类。将各自的特征矩阵串联起来，构建一个(稀疏的)块对角矩阵，其中每个块对应于一个图实例的邻接矩阵。对于pooling(如果是图级输出而不是节点级输出)，最好指定一个简单的pooling矩阵，从各自的图实例中收集特征，如下图所示:

有错误的地方还望不吝指出，欢迎进群交流GNNs&GCNs（入群备注信息!!!，格式：姓名 -（学校或其他机构信息）- 研究方向）。

参考

[1] (本文参考文献) Thomas N. Kipf, Max Welling. Semi-Supervised Classification with Graph Convolutional Networks. ICLR 2017.
[2] 官方博客:Graph Convolutional Networks
[3] 知乎：图卷积网络(GCN)新手村完全指南
[4] GCN (Graph Convolutional Network)图卷积网络解析
[5] 关于图卷积网络GCN的一点理解
[6] 浅析图卷积神经网络
[7] Graph Convolutional Network介绍及简单实现

资料下载

图卷积相关ppt下载