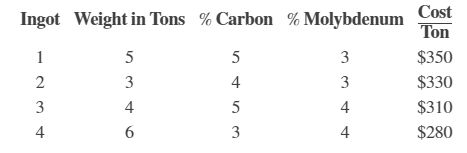Matlab 离散优化: Mixed-Integer Linear Programming Basics: Solver-Based
Mixed-Integer Linear Programming Basics: Solver-Based
- Poblem Description
- MATLAB® Formulation
- Solve Problem
本文全文翻译自Matlab官方教程:Mixed-Integer Linear Programming Basics: Solver-Based
这个例子展示了如何解决一个混合整数线性问题。虽然不复杂,但该示例显示了使用intlinprog语法构造问题的典型步骤。
对于这个问题的基于问题的方法,参见:Mixed-Integer Linear Programming Basics: Problem-Based
Poblem Description
你想把不同化学成分的钢混合起来,得到25吨具有特定化学成分的钢。结果应含有5%的碳和5%的钼(按重量计),即25吨*5%=1.25吨碳和1.25吨钼。其目的是尽量降低钢的混合成本。
这个问题摘自Carl Henrik Westerberg,Bengt Bjorklund和Eskil Hultman,“瑞典钢铁厂混合整数规划的应用”,接口1977年2月第7卷,第2期,第39-43页,摘要见https://doi.org/10.1287/inte.7.2.39。
有四块钢锭可供购买,每个钢锭只有一个可用。

要解决这个问题,首先要确定控制变量。取变量 x ( 1 ) = 1 x(1)=1 x(1)=1表示购买铸锭1, x ( 1 ) = 0 x(1)=0 x(1)=0表示不购买铸锭。类似地,变量 x ( 2 ) x(2) x(2)到 x ( 4 ) x(4) x(4)是指示您是否购买锭2到4的二进制变量。
变量 x ( 5 ) x(5) x(5)到 x ( 7 ) x(7) x(7)是以吨为单位购买的合金1、2和3的数量, x ( 8 ) x(8) x(8)是以吨为单位购买的废钢数量。
MATLAB® Formulation
通过指定intlinprog的输入来求解问题。intlinprog语法:
[x,fval] = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)
为intlinprog创建从第一个(f)到最后一个(ub)的输入。
f是cost系数的向量,代表铸锭成本的系数是铸锭重量乘以每吨成本。
f = [350*5,330*3,310*4,280*6,500,450,400,100];
整数变量是前四个:
intcon = 1:4;
提示:要指定二进制变量,请在intcon中将这些变量设置为整数,并给它们一个下界0和上界1。
该问题没有线性不等式约束,因此A和b是空矩阵[]。
A = [];
b = [];
这个问题有三个等式约束。首先是总重量是25吨:
5*x(1) + 3*x(2) + 4*x(3) + 6*x(4) + x(5) + x(6) + x(7) + x(8) = 25
第二个限制是碳的重量是25吨的5%,即1.25吨:
5*0.05*x(1) + 3*0.04*x(2) + 4*0.05*x(3) + 6*0.03*x(4)
+ 0.08*x(5) + 0.07*x(6) + 0.06*x(7) + 0.03*x(8) = 1.25
第三个限制是钼的重量是1.25吨:
5*0.03*x(1) + 3*0.03*x(2) + 4*0.04*x(3) + 6*0.04*x(4)
+ 0.06*x(5) + 0.07*x(6) + 0.08*x(7) + 0.09*x(8) = 1.25
以矩阵形式指定 A e q ∗ x = b e q Aeq*x=beq Aeq∗x=beq约束:
Aeq = [5,3,4,6,1,1,1,1;
5*0.05,3*0.04,4*0.05,6*0.03,0.08,0.07,0.06,0.03;
5*0.03,3*0.03,4*0.04,6*0.04,0.06,0.07,0.08,0.09];
beq = [25;1.25;1.25];
每个变量的下界为零。整型变量的上界是1。
lb = zeros(8,1);
ub = ones(8,1);
ub(5:end) = Inf; % No upper bound on noninteger variables
Solve Problem
既然已经有了所有的输入,就调用解算器。
[x,fval] = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub);
输出:
LP: Optimal objective value is 8125.600000.
Cut Generation: Applied 3 mir cuts.
Lower bound is 8495.000000.
Relative gap is 0.00%.
Optimal solution found.
Intlinprog stopped at the root node because the objective value is within a gap
tolerance of the optimal value, options.AbsoluteGapTolerance = 0 (the default
value). The intcon variables are integer within tolerance,
options.IntegerTolerance = 1e-05 (the default value).
观察输出:
x,fval
x = 8×1
1.0000
1.0000
0
1.0000
7.2500
0
0.2500
3.5000
fval = 8.4950e+03
最佳购买价格为8495美元。购买1号、2号和4号钢锭,但不要购买3号钢锭,购买7.25吨合金1、0.25吨合金3和3.5吨废钢。
设置 i n t c o n = [ ] intcon=[] intcon=[]以查看在没有整数约束的情况下解决问题的效果。解决方案不同,而且不现实,因为您不能购买一小部分铸锭。