算法设计与分析:贪心算法 - 排课问题(DP与贪心的区别与应用)
文章目录
- 前言
- 贪心算法概念
- 排课问题
- 问题描述与分析
- 动态规划求解
- 简化问题应用贪心算法
- 总结
本文参考UCAS卜东波老师算法设计与分析课程撰写
前言
前面两大章节的内容分治思想与动态规划暂时告一段落,遇到问题如何观察问题,找寻解决的方案是我们关心的点。下面的关系图诠释了问题的观察步骤与解决方案选择:
正面可解?
在动态规划的基础上又可以根据我们的需求选择使用高级动态规划,现在再进一步,在动态规划的基础上依据是否有贪心选择的性质,决定是否采用贪心算法。
贪心算法概念
贪心算法与动态规划十分相像,只不过在动态规划的基础上多了一层贪心选择幸性质,每一次的贪心,我们都是求局部最优解,将这些解组合成了全局最优,当然这点能够成立的前提是问题具有贪心选择性质,我们利用排课问题来具体阐述其差别。
排课问题
问题描述与分析
- 一间教室被多门课程在不同时段使用,给定第i节课 A i A_i Ai从 S i S_i Si开始上,到 F i F_i Fi结束,上第i门课的学生数量是 W i W_i Wi,问如何排课能让尽可能多的学生上课?
考虑问题中的矛盾点在于,时间段相交的课程会冲突,因此,安排的课必须是两两不相交的,且要使得上课学生数量最大。下面是一个例子(引用课件)

- 方案1:选课集合 S 1 = { A 1 , A 3 , A 5 , A 8 } S_1 = \{A_1,A_3,A_5,A_8\} S1={A1,A3,A5,A8},则上课总人数 B ( S 1 ) = 1 + 4 + 3 + 3 = 11 B(S_1)= 1+4+3+3=11 B(S1)=1+4+3+3=11
- 方案2:选课集合 S 2 = { A 2 , A 4 , A 7 , A 9 } S_2 = \{A_2,A_4,A_7,A_9\} S2={A2,A4,A7,A9},则上课总人数 B ( S 2 ) = 5 + 2 + 1 + 5 = 13 B(S_2) = 5+2+1+5 = 13 B(S2)=5+2+1+5=13
- 方案3:…
如何快速地找出众多方案中人数最多的,是我们的目标。显然这已经是一个最优化问题。
动态规划求解
首先,最简单的情况n=1,2的时候很好分析,所以先思考问题是否可分解子问题?鉴于前面已经确认是最优化问题,所以我们分解按照多步决策的方向分解。以下为多步决策过程:
-
A 9 A_9 A9上不上?
- 上:则新的可选时间段缩短到 A 9 A_9 A9上课前,递归调用剩下的所有在时间段内课程
- 不上:则时间段不变,将 A 9 A_9 A9去除,递归调用 A 1 . . . A 8 A_1...A_8 A1...A8
剩下的决策过程其实是一样的,但是这里有一个小问题,如何快速找出所有在 A 9 A_9 A9上课前的所有课程?如果在选定 A 9 A_9 A9上了之后,再循环遍历挑出来,那每一次决策都要遍历,时间复杂度过高。因此,我们预先对所有课程按照下课时间排序(实际上前面的例子已经排好序),这样我们很容易找到下课在 A 9 A_9 A9上课前的课程。
这里做一些定义,我们采用了动态规划的方式,自然要定义动态转移方程。设对课程 A 1 , . . . , A i A_1,...,A_i A1,...,Ai的最优选择结果是 O P T ( i ) OPT(i) OPT(i),在第i节课上课前的最近下课课程编号是 p r e ( i ) pre(i) pre(i)(例如 p r e ( 9 ) = 7 pre(9) = 7 pre(9)=7 ),我们得到转移方程如下:
O P T ( i ) = { O P T ( p r e ( i ) ) + W i 选 择 A i O P T ( i − 1 ) 不 选 A i OPT(i) = \begin{cases} OPT(pre(i)) +W_i & 选择A_i \\ OPT(i-1) & 不选A_i \end{cases} OPT(i)={OPT(pre(i))+WiOPT(i−1)选择Ai不选Ai
上述过程是很常规的动态规划方法解决,对于每个决策有两个选项(选/不选),然后对应每个选项再递归调用。将该过程绘制成决策图如下:

容易得到伪代码如下:
这部分较好理解,不多赘述,总时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
简化问题应用贪心算法
实际上上面的DP方法已经解决了这个问题,但我们在开头的关系图中考虑了在DP的基础上能否找出贪心规则进一步使用贪心算法。在用贪心解决问题之前,先考虑另一种不一样的动态规划方法,前面我们是对每门课进行多步决策(选不选这门课),实际上最终的解可以表示成 X = [ 1 , 0 , 0 , 1 , . . . , 1 ] X=[1,0,0,1,...,1] X=[1,0,0,1,...,1]的形式,其中1表示选,0表示不选。如果我们从解的角度出发,我们只考虑那些要选的课,那么第一次决策就转换成了,我第一次要选哪一门课。这有9个选项,对于每一个选项,我在对除去该课和与该课冲突的课程的子集中继续递归调用即可。将其转换成图示如下:

我们得到动态转移方程如下:
O P T ( S ) = max A i ∈ S { O P T ( S ′ ) + W i } OPT(S) = \max_{A_i\in S}\{OPT(S')+W_i\} OPT(S)=Ai∈Smax{OPT(S′)+Wi}
其中,S是当前可选课程集合,S’是除去第i节课程和与该课程冲突的课程集合。
由此我们得到伪代码如下:

这相当于把所有的可能组合都枚举了出来,而对于集合元素数n的可能组合有 2 n 2^n 2n种,因此时间复杂度为 O ( 2 n ) O(2^n) O(2n),这与我们平常对动态规划的时间认知有所不同,主要是缺乏了DP数组存储重复计算的结果,例如我先选1,再选2和先选2再选1应该是一样的效果,这里进行了重复计算。为了引入贪心算法,下面我们考察一个简单的特例:
-
假设每门课均只有一个人上,上面的例子转换后如下所示:
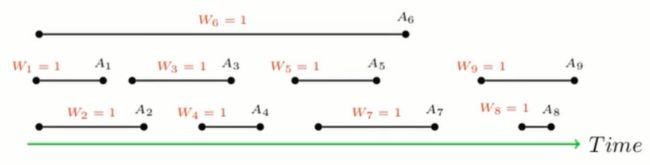
前面的动态规划方法枚举了所有可能情况,这是导致时间耗费很大的一个原因,而在贪心中直接选择最早下课的那门( A 1 A_1 A1),因为它必然会出现在最优解中,不再枚举其他的情况。下面是简单的证明:- 反证法
假设存在一个最优解不包括 A 1 A_1 A1,例如该最优解是 A 2 , A 4 , A 6 , A 7 A_2,A_4,A_6,A_7 A2,A4,A6,A7,显然我们可以用 A 1 A_1 A1替换掉 A 2 A_2 A2,构造新的最优解 A 1 , A 4 , A 6 , A 7 A_1,A_4,A_6,A_7 A1,A4,A6,A7,这里人数未发生变化( W i = 1 W_i=1 Wi=1),新的最优解中就有了 A 1 A_1 A1
这个方法好啊!这相当于第一次原本要考虑1-9,现在直接扔掉2-9,选中了1,瞬间减少了时间。而在第1门被选定之后,在剩下的课程中,我们依然每次都找最早下课的,但要求选的课不能和已选的冲突(上课时间要晚于最近选择的下课时间)。这样,我们相当于只用做一次循环遍历就可以找出最优解,样例(来源课件)如下:

解释一下选择的过程,首先按照下课时间对课程排序,循环遍历,发现B是最早下课,将B安排上,到C,C虽然是新最早下课,但与B冲突,不安排,A也同理,一直到E,安排上,D,F,G与E冲突,不安排,H可行,安排上。
总的时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn)
- 反证法
这里首先解释一点,原本的排课问题只能通过传统的动态规划方法快速解决,无法直接应用贪心,但是如果问题变了一些条件(每个课的学生数量相同),我们就可以用贪心解决,因为每一次只用找最早下课的即可(局部最优)。贪心算法相当于解决了原问题的一个简化版本,你可能会问,那我为什么不直接用动态规划好了?首先,对比代码量,显然可以发现贪心实现地更为简洁,其次,贪心不需要额外的存储空间(DP数组),有点杀鸡不需用牛刀的感觉。
总结
本文通过排课问题,简单阐述了贪心问题与动态规划之间的联系。它们的相似点如下:
- 都针对最优化问题,因此看到最优化问题,首先想到动态规划与贪心
- 最优子结构,动态规划与贪心都要寻求最优子结构,即子问题的最优解可用于组合成原问题的最优解
- 所有的贪心算法都可以找到一个笨拙动态规划的版本(本文中是 O ( 2 n ) O(2^n) O(2n))
而它们的不同点如下:
-
动态规划需在每一步决策时枚举所有可能的选项,只有子问题解决后,决策才能做出判断
例如 A 9 A_9 A9选与不选先要询问前面最优选择情况,文中例子是选的情况询问 A 1 . . . A 7 A_1...A_7 A1...A7,不选的情况询问 A 1 . . . A 8 A_1...A_8 A1...A8 -
贪心算法则不必枚举所有可能情况,它在当前决策下就直接选定了局部最优,而不考虑子问题的选择
这一方面提高了他的速度,另一方面也让它受限较大(在本例中就是每门课学生人数都要相等),这也是贪心选择的性质
如果你觉得文章对你有用,不妨顺手点个赞哦~
- 上一篇:算法设计与分析:动态规划(4)- 序列联配问题(观察回溯路径)
- 下一篇:算法设计与分析:贪心算法(2)- 最短路问题(DP到贪心的优化)
- 目录

