程序员的数学系列（一）

程序员的数学系列阅读笔记，第一部分介绍数学基础，还有一些有趣的数学问题

第1章 0的故事

无即是有，zero matters

10进制

2503

2×103+5×102+0×101+3×100 2 × 10 3 + 5 × 10 2 + 0 × 10 1 + 3 × 10 0

2进制

1100

1×23+1×22+0×21+0×20 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 0 × 2 0

基数转换

• 2进制表示12
  
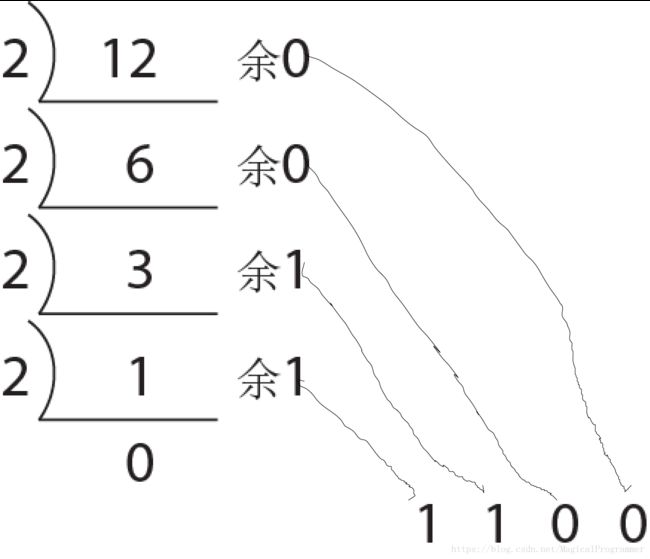
  计算机计算过程： (21+19)−→−−−−−转换为2进制(10101+10011)−→−−−−−−使用2进制计算(101000)−→−−−−−转换为10进制(40) ( 21 + 19 ) → 转 换 为 2 进 制 ( 10101 + 10011 ) → 使 用 2 进 制 计 算 ( 101000 ) → 转 换 为 10 进 制 ( 40 )

指数法则

103−→110102−→110101−→110100=1 10 3 → 1 10 10 2 → 1 10 10 1 → 1 10 10 0 = 1

25−→1224−→11023−→1222−→1221−→1220−→122−1=12 2 5 → 1 2 2 4 → 1 10 2 3 → 1 2 2 2 → 1 2 2 1 → 1 2 2 0 → 1 2 2 − 1 = 1 2

指数法则

Na×\Nb=Na+b(N≠0) N a × \N b = N a + b ( N ≠ 0 )

0所起的作用

• 占位

  2503， 表示10位什么都没有

• 统一标准，简化规则

  按位计数就可统一写为

  ak×10k a k × 10 k

  n=3,a3=2,a2=5,a1=0,a0=3→2503 n = 3 , a 3 = 2 , a 2 = 5 , a 1 = 0 , a 0 = 3 → 2503

• 0表示没有

  有规律地服用一种胶囊，每4天停用一次。也就是3天服用，1天停用。于是每4粒胶囊中有1粒是“没有药效”的假胶囊，放入标有日期的盒子并放入每天需要服用的药，以后就只用每天服用。

第2章 逻辑

真与假的二元世界

逻辑是消除歧义得工具

兼顾完整性和排他性

没有遗漏，没有重复

逻辑非

A A	¬A ¬ A
true	false
false	true

双重否定表肯定

A A	¬A ¬ A	¬¬A ¬ ¬ A
true	false	true
false	true	false

逻辑与

A∧B(AandB) A ∧ B ( A a n d B )

真值表

A A	B B	A∧B A ∧ B
true	true	true
true	false	false
false	true	false
false	false	false

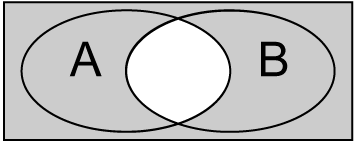
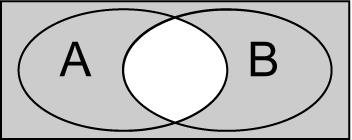
文氏图

文氏图表示 ¬(A∧B) ¬ ( A ∧ B )

逻辑或

A∨B(AorB) A ∨ B ( A o r B )

真值表

A A	B B	A∨B A ∨ B
true	true	true
true	false	true
false	true	true
false	false	false

文氏图

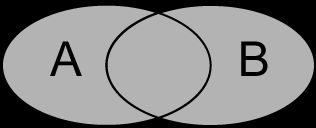
文氏图表示 (¬A)∨(¬B) ( ¬ A ) ∨ ( ¬ B )

异或

A⊕B A ⊕ B
真值表

A A	B B	A∨B A ∨ B
true	true	false
true	false	true
false	true	true
false	false	false

文氏图

相等

A=B A = B
真值表

A A	B B	A=B A = B
true	true	true
true	false	false
false	true	false
false	false	true

文氏图

¬(A⊕B)→(A=B) ¬ ( A ⊕ B ) → ( A = B )

蕴含—若A则B

A⟹B A ⟹ B
真值表

A A	B B	A⟹B A ⟹ B
true	true	true
true	false	false
false	true	true
false	false	true

A为true时，仅当B为false时 A⟹B A ⟹ B 才为false
A为false时， A⟹B A ⟹ B 恒为true

此为逻辑上“如果”的定义

我们平时说的“若A则B”有两种情况

1. 若A为true，则B也为true。若A为false，则B也为false
2. 若A为true，则B也为true。但是，若A为false时，则B为true/false都可以（对B没有任何影响）

在逻辑上二者的区别在于，1是 A=B A = B ，2是 A⟹B A ⟹ B

文氏图， (¬A)∨B ( ¬ A ) ∨ B 的文氏图也是这样，于是 (¬A∨B)⟺(A⟹B) ( ¬ A ∨ B ) ⟺ ( A ⟹ B ) ，二者等价

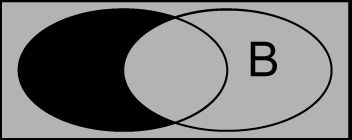
B⟹A B ⟹ A 为 A⟹B A ⟹ B 的逆命题，逆命题不一定为真

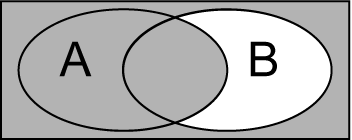
(¬B)⟹(¬A) ( ¬ B ) ⟹ ( ¬ A ) 的文氏图也和 A⟹B A ⟹ B 的相同(二者等价)，即， ((¬B)⟹(¬A))⟺(A⟹B) ( ( ¬ B ) ⟹ ( ¬ A ) ) ⟺ ( A ⟹ B )
此为 A⟹B A ⟹ B 的逆否命题

德·摩根定律

(¬A)∨(¬B)=¬(A∧B) ( ¬ A ) ∨ ( ¬ B ) = ¬ ( A ∧ B )

(¬A)∧(¬B)=¬(A∨B) ( ¬ A ) ∧ ( ¬ B ) = ¬ ( A ∨ B )

三值逻辑的德·摩根定律

(!A)∨(!B)=!(A∧B) ( ! A ) ∨ ( ! B ) = ! ( A ∧ B )
(!A)∧(!B)=!(A∨B) ( ! A ) ∧ ( ! B ) = ! ( A ∨ B )

if (!(x >= 0 && y >= 0)) {
    .....
}
// equal to
if (x < 0 || y < 0) {
    ....
}

本章小结

逻辑的各种表现形式

if语句将世界一分为二，条件成立的世界和条件不成立的世界

第3章 余数

周期性和分组

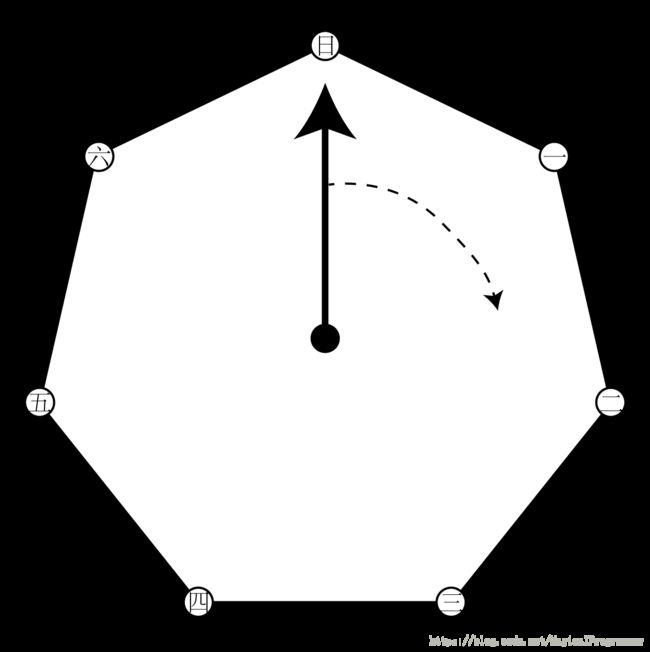
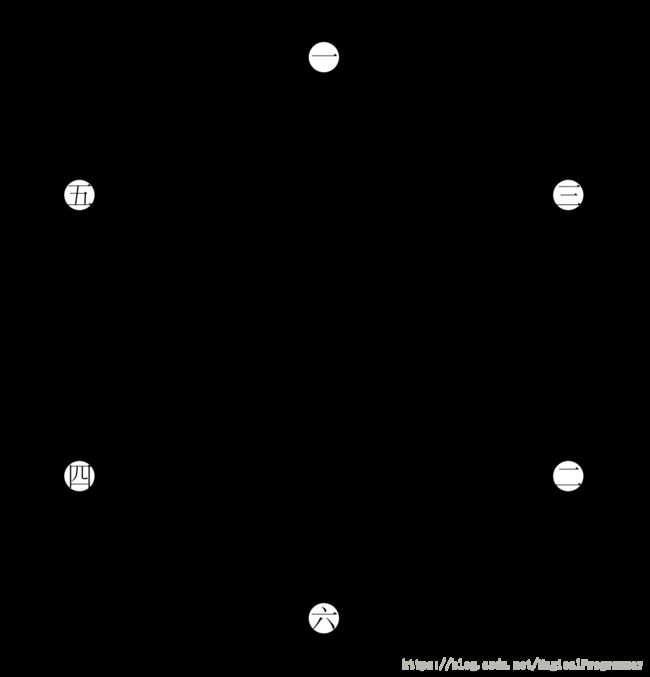
星期数问题

今天是星期日，100天后是星期几？

1亿天呢？

10100 10 100 天后呢？

100÷7=14...2 100 ÷ 7 = 14...2

因此100天后是星期二

108÷7=14285714...2 10 8 ÷ 7 = 14285714...2

因此1亿天后是星期二

0的个数	数字	除以7的余数	星期数
0	1	1	一
1	10	3	三
2	100	2	二
3	1000	6	六
4	10000	4	四
5	100000	5	五
6	1000000	1	一
7	10000000	3	三
8	100000000	2	二
9	1000000000	6	六
10	10000000000	4	四
11	100000000000	5	五
12	1000000000000	1	一

余数以1、3、2、6、4、5···的顺序循环

100÷6=16...4 100 ÷ 6 = 16...4

余数为4，因此 10100 10 100 天后是星期四

直观地把握规律

第n天是星期几

第 10n 10 n 天是星期几

乘方得思考题

1234567987654321 1234567 987654321 的个位数是什么

试算：

12345670 1234567 0 的个位数= 70 7 0 的个位=1

12345671 1234567 1 的个位数= 71 7 1 的个位=7

12345672 1234567 2 的个位数= 72 7 2 的个位=9

12345673 1234567 3 的个位数= 73 7 3 的个位=3

12345674 1234567 4 的个位数= 74 7 4 的个位=1

12345675 1234567 5 的个位数= 75 7 5 的个位=7

12345676 1234567 6 的个位数= 76 7 6 的个位=9

12345677 1234567 7 的个位数= 77 7 7 的个位=3

12345678 1234567 8 的个位数= 78 7 8 的个位=1

12345679 1234567 9 的个位数= 79 7 9 的个位=7

周期为4，用987654321对4取余0、1、2、3其中之一，它们分别对应1、7、9、3

余1，所以个位数是7

黑白棋通信

1. 桌面随机7枚黑白棋棋子，魔术师蒙着眼睛，看不到棋子
   
2. 魔术师徒弟看完7枚棋子后，又放进一枚，这时桌面有8枚棋子
   
3. 观众可以选择翻转一枚或者不翻转任何棋子，此时观众和徒弟都不能说话
4. 魔术师观察8枚棋子，马上就能判断观众是不是翻转了棋子