FIR数字滤波器的FPGA实现(一)-FIR滤波器基本原理

(一)FIR数字滤波器的FPGA实现-FIR滤波器基本原理

---

---

  对于FIR滤波器主要涉及到滤波器的设计和滤波器的实现，设计和实现的区别如下图所示：

  实现是 forward problem，设计是 inverse problem

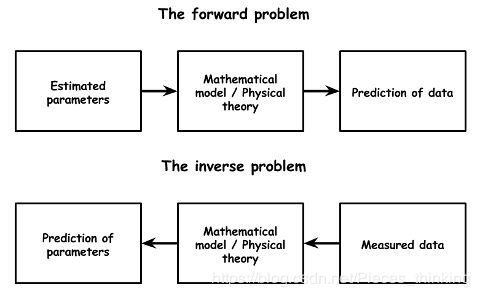
               What are inverse problems?

  本文主要涉及到FIR滤波器的实现，在实现的过程中，h[k]都是已知的，而h[k]的求解一般是设计的过程。具体内容包括，FIR滤波器的基本原理，串行FIR滤波器设计（此设计为滤波器实现的“设计”和FIR滤波器的设计不同，自行理会），并行FIR滤波器设计，串并FIR滤波器设计，分布式FIR滤波器设计，快速卷积型 FIR 滤波器、多通道 FIR 滤波器、多频响 FIR 滤波器。对于快速卷积型 FIR 滤波器、多通道 FIR 滤波器、多频响 FIR 滤波器会简单介绍，其中串行、并行、串并、分布式FIR滤波器设计会给出相应源码和仿真模型，如果条件允许会抽出一个源码在FPGA上运行，并进行实验分析。

---

1 FIR滤波器基本原理

  在数字处理中，滤波占有重要的地位。数字滤波在语音和图像处理、HDTV(High-Definition Television)、模式识别、谱分析等应用中经常用到。与模拟滤波相比，数字滤波具有很突出的优点。例如它可以满足滤波器对幅度和相位特性的严格要求，可以避免模拟滤波所无法克服的电压漂移、温度漂移和噪声等问题。
  根据数字滤波器冲激响应函数的时域特性，可将数字滤波器分为无限长冲激响应(IIR)滤波器和有限长冲激响应(FIR)滤波器两种。由于FIR系统只有零点、系统稳定，便于实现FFT算法、运算速度快、线性相位的特性和设计更为灵活等突出优点而在工程实际中获得广泛应用[1]。
  FPGA (Field Program Gate Array)是可编程逻辑器件中一种比较复杂的形式，它正处于革命性数字信号处理的前沿。全新的FPGA系列正在越来越多的替代ASIC(Application-Specific Integrated Circuit)和PDSP(Programmable Digital signal processors)用作前端数字信号处理的运算。FPGA具有许多与ASIC相同的特点。例如:在规模、重量和功耗等方面都有所降低。而且吞吐量更高、能更好的防止未授权复制、元器件和开发成本的进一步降低，开发时间也大大缩短。还具有在线路中可重复编程的特性。
  它允许电路设计者利用基于计算机的开发平台，经过设计输入、仿真、测试和校验，直至达到预期的效果，从而可以产生更为经济的设计。更吸引人的是，采用FPGA器件可以将原来的电路板级产品集成为芯片级产品。正如我们现在所看到的，随着FPGA在数字信号处理中的大规模应用，正在日渐深入地影响我们的生产和生活，也必将在这领域引起深刻的变革。
  如今FIR滤波器的硬件设计有多种实现方法。第一种是采用单片机来实现，但单片机的处理速度比较慢。第二种是采用专用的DSP芯片，但是DSP的串行指令执行发式，使其工作速度和效率大打折扣，因此当滤波器的系数增加或字长增长时，计算时间会成倍增加，从而降低了最大有效数据采样率。而且在一些高速的应用中，系统性能不断增长，而DSP性能的提高却落后于需求的增长。第三种是采用市场上通用的FIR滤波器集成电路，但由于它的通用性，很难满足设计者独特的要求。第四种是采用可编程逻辑器件(PLD)的方法来实现。
  可编程逻辑器件在电子技术领域中的应用，为数字硬件电路系统的设计带来了极大的灵活性。由于可编程逻辑器件可以通过软件编程而对其硬件结构和工作方式进行重构，使得硬件的设计可以如同软件设计那样方便快捷。这一切极大地改变了传统的数字硬件电路系统设计方法、设计过程、乃至设计观念。纵观可编程逻辑器件的发展史，它在结构原理、集成规模、下载方式、逻辑设计手段等方面的每一次进步都为现代电子设计技术的革命与发展提供了不可或缺的强大动力。

---

---

1.1 FIR滤波器的结构及设计

  数字滤波器通常都是应用于修正或改变时域或频域中信号的属性。最为普通的数字滤波器就是线性时间不变量(linear time- invariant ,LTI)滤波器。LTI与其输入信号之间相互作用，经过一个称为线性卷积的过程。表示为y=f x,其中f是滤波器的脉冲响应，x是输入信号，而y是卷积输出。线性卷积过程的正式定义如下:

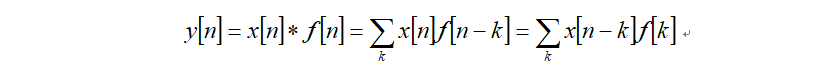
  LTI数字滤波器通常分成有限脉冲响应(finite impulse response，也就是FIR)和无限脉冲响应(infinite impulse response，也就是IIR)[3]两大类。顾名思义,FIR滤波器由有限个采样值组成，将上述卷积的数量降低到在每个采用时刻为有限个。而IIR滤波器需要执行无限数量次卷积。研究数字滤波器的动机就在于它们正日益成为一种主要的DSP操作。数字滤波器正在迅速的代替传统的模拟滤波器，后者是利用RLC元器件和运算放大器实现的。模拟原型设计只能应用在IIR设计之中，而F1R通常采用直接的计算机规范和算法进行分析的。

---

1.1.1 FIR数字滤波器基础

  数字滤波器(DF)是个离散系统，它所处理的对象是用序列表示离散信号或数字信号。DF的因果离散系统函数可表示成:

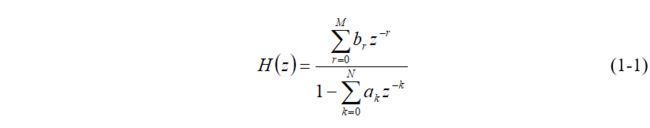
  其常系数线性差分方程为:

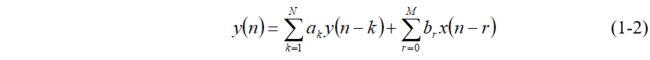
  可以看出，数字滤波器是把输入和之前输出的序列经过一定的运算变换成输出的序列。大多数普通的数字滤波器都是LTI滤波器，对于FIR系统，其系统函数仅有零点(除Z=0的极点外)，因此FIR系统的差分方程可以表示为:

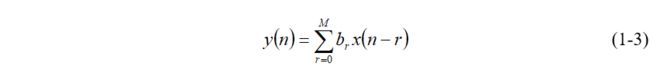
  转移函数为：

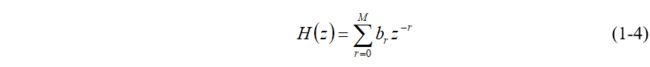
  由(1-3)式可知，系统的脉冲响应是因果序列，因为其输出仅与即时输入以及过去的输入数据有关，而与过去的输出数据没有直接的关系，所以FIR滤波器是因果的，是物理可实现的系统，因而它在实际中往往采用非递归(无反馈作用)形式的结构来实现。人们把用非递归形式实现的FIR滤波器叫做非递归型滤波器。而且，由(1-3)式还可以知道，此系统的脉冲响应是绝对可加的，所以FIR滤波器总是稳定的。
  FIR滤波器相对于IIR滤波器有很多独特的优越性，在保证满足滤波器幅频响应的同时，还可以获得严格的线性相位特性。对于非线性FIR滤波器一般可以用IIR滤波器来替代。由于在数据通信、语音信号处理、图像处理以及自适应等领域往往要求信号在传输过程中不允许出现明显得相位失真，而IIR存在明显得频率色散的问题，所以FIR滤波器得到了更广泛的应用。

---

1.1.2 FIR数字滤波器的基本结构

  FIR滤波器的构成形式主要有直接型、级联型、线性相位FIR滤波器的结构等，下面分别加以讨论。

1.直接型结构

  图1-1给出了N阶LTI型FIR滤波器的图解。可以看出FIR滤波器是有一个 “抽头延迟线”加法器和乘法器的集合构成的。传给每个乘法器的操作数就是一个FIR系数，显然也可以称作“抽头权重” 因此该结构也称为“横向滤波器” 。

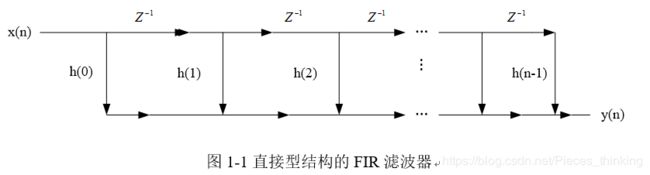
  直接FIR模型的一个变种称为转置式FIR滤波器，它是根据转置定理定义如果将网络中所有支路的方向倒转，并将输入x (n)和输出y (n)互换，则其系统传递函数H(z)不变。其转置结构见图1-2[4]。

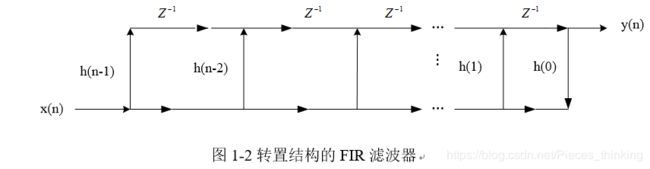
  将图 1-2 所示结构的加法操作方向翻转并使输入、 输出数据位于同侧， 即可得到图 1-3 所示的结构， 称之为输入、 输出位于同侧的直接型结构。

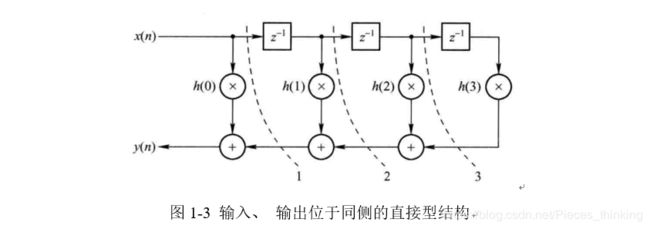
  对图1-3所示结构进行如下操作： 以图中的 1、 2、 3 号虚线为界搬移延时单元。 例如，对 1 号虚线右侧的延时单元搬移可得图 1-4 所示结构。 搬移前后对比可知， 路径 1 的总延时并没有改变， 改变的只是延时单元的位置， 这就是所谓的重定时 (Retiming) 技 术。
  同样的操作应用于 2、 3 号虚线右侧的延时单元， 可得图 1-5 所示的输入、 输出位于同侧的转置型 FIR 滤波器结构。

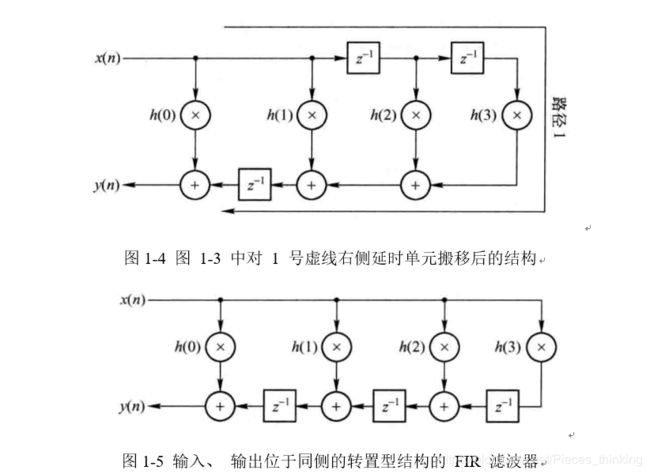
  当然， 也可使输入、 输出分别位于两侧， 即可得图 1-6 所示的结构。 此时， 最大的不同是滤波器系数的排列顺序进行了调整。

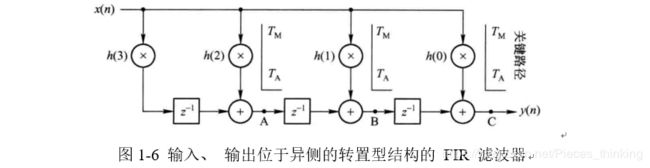
  图 1-6 所示的 4 抽头转置结构其转移函数可以用另一种方式表示， 如式 (1-5) 所示。

  与图 1-3 的直接型结构对比， 转置型结构的关键路径进一步缩短。
  对图 1-3 所体现的数据流进行分析， 结果如表 1-1 所示。

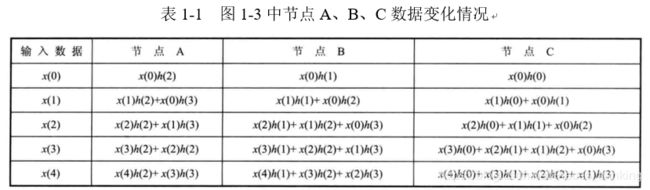
  转置型结构并没有引入过多的延时。 进一步而言， 直接型结构与转置型结构两者由输入到输出所需时间是一致的， 即输入为 x( n ) 时输出y(n)。
  转置式滤波器通常是指FIR滤波器的实现。该滤波器的优点在于我们不再需要给x(n)提供额外的移位寄存器，而且也不必要为达到高吞吐量给乘积的加法器(树)添加额外的流水线级。

2.级联型

  如将(1-4)式分解为二阶实系数因子形式:

  便可得二阶级联结构。这种结构每一节控制一对一零点，因而在需要控制传输零点时可以采用。但相应的滤波系数增加，乘法运算次数增加，因此需要较多的存储器，运算时间也比直接型增加。

3.线性相位FIR系统的结构

  在许多应用领域，例如通信和图像处理中，在一定频率范围内维持相位的完整性是一个期望的系统属性。因此，设计能够建立线性相位频率功能的滤波器是必须遵循的规范。系统相位线性度的标准尺度就是“组延迟”,其定义为[5]:

  完全理想的线性相位滤波器对于一定频率范围的组延迟是一个常数。可以看到如果滤波器是对称或者反对称的，就可以实现线性相位。
  线性相位(相移)表示一个系统的相频特性与频率成正比，由于不同频率传输速度都一样，所以信号通过它产生的时间延迟等于常数k，所以不出现相位失真,对一个数字系统来说，即φ（w） =-kw。
  假设一个离散时间系统的幅频特性等于1，则当信号x(n)通过该系统后，其输出y(n)的频率特性：

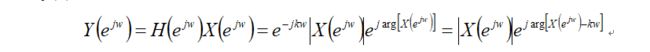
  所以y(n) = x(n-k)，这样输出y (n)等于输入在时间上的唯一，达到了无失真输出的目的。
  可以证明，线性相位条件为:

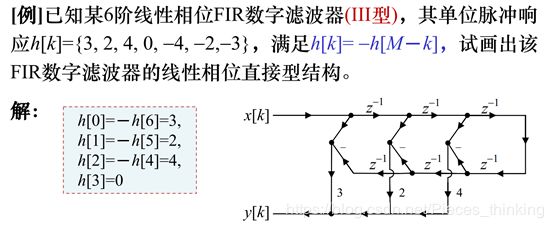
• h(n)=h(N-1-n) 偶对称
• h(n)=-h(N-1-n)奇对称

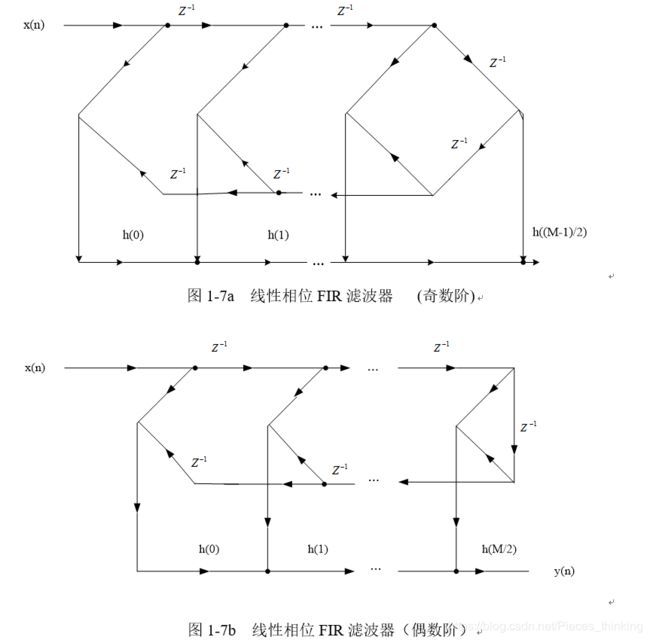
  即如果单位脉冲响应h (n)为实数，且具有偶对称或奇对称性，则FIR数字滤波器具有严格的线性相位特性。其对称中心在n=（N-1）/2处。当N分别为奇数和偶数时，其网络结构可以分别用图1-7 (a) , (b)的信号流图来实现。由该信号流图可以看出，线性相位结构比图1-2的直接实现形式少用个乘法器(或乘法运算)。

举例如下：

---

1.1.3 FIR数字滤波器的设计

  FIR滤波器设计方法是以直接逼近所需离散时间系统的频率响应为基础。设计方法包括窗函数法和最优化方法(等同纹波法)，其中窗函数方法是设计FIR数字滤波器是最常用的方法之一。

1.窗函数法

  任何数字滤波器的频率响应H(e^jw) 都是w的周期函数，它的傅立叶级数展开式为:

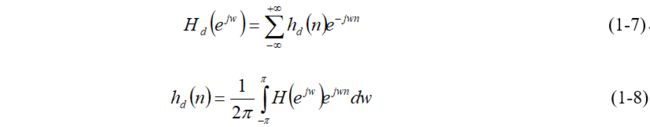
  傅立叶系数h(n)实际上就是数字滤波器的冲击响应，由于h(n)可能是无限长序列且为非因果响应，是物理不可实现的。为此要寻找一个因果的h(n)，在相应的误差准则下最近逼近h(n)。窗函数法设计的初衷是使设计的滤波器频率特性H(e^jw)在频域均方误差最小意义下进行逼近，即:

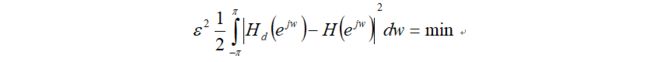
  窗函数法就是用被称为窗函数的有限加权序列G_N(n)来修正式(1-8)，则所需h (n)表示为:

  G_N(n)是有限长序列，当n>N-1及n<0时，G_N(n)=0，这里我们仅以冲激响应对称即h(n)=h(N-1-n)(n=0,1,2,…N-1)时低通滤波器为例进行说明。低通滤波器的频率响应函数H(e^jw)如下式所示:

  在w<|w|<π 时为0，其中w为对抽样频率归一化的角频率，w_c 为归一化截止角频率。利用反傅立叶变换公式求出式(1-10)对应的冲激响应h(n)为：

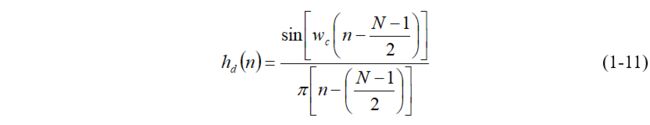
  几种窗函数及其窗函数选择原则:
  设计FIR滤波器常用的窗函数有:矩形窗函数、三角窗（bartlett）函数、汉宁(Hanning)窗函数、海明(Hamming)窗函数、布莱克曼(Blackman)窗函数和凯塞(Kaiser)窗函数，具体性能指标可参看表1-2[5]。

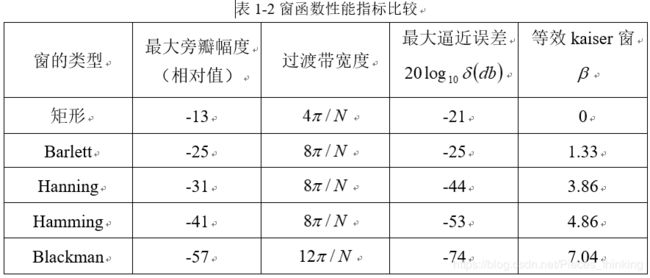
  窗函数的选择原则是:

• (1)具有较低的旁瓣幅度，尤其是第一旁瓣幅度。
• (2)旁瓣幅度下降速度要快，以利于增加阻带衰减。
• (3)主瓣宽度要窄，以获得较陡的过渡带。

  通常上述几点很难同时满足，当选用主瓣宽度较窄时,虽然得到较陡的过渡带，但通带和阻带的波动明显增加;当选用最小的旁瓣幅度时，虽然能得到匀滑的幅度响应和较小的阻带波动,但是过渡带加宽。因此,实际选用的窗函数往往是它们的折中。在保证主瓣宽度达到一定要求的情况下,适当地牺牲主瓣的宽度来换取旁瓣波动的减少。

2.等同纹波设计方法

  窗函数存在某些缺陷。首先,在设计中不能将边缘频率w_p 和w_x 精确的给定;也就是意味着在设计完成之后无论得到何值都必须接受。其次，不能够同时标定纹波因子δ₁ 和δ₂；在窗函数设计法上只能设定δ₁ =δ₂ 。最后，近似误差在频带区间上不是均匀分布的，在靠近频带边缘误差愈大，远离频带边缘误差愈小。
  一种非常有效的解决这种问题的FIR滤波器就是等同纹波FIR滤波器。对于线性相位FIR滤波器来说，有可能导得一组条件，对这组条件能够证明，在最大近似误差最小化的意义下，这个设计时最优的。具有这种性质的滤波器就称为等同纹波滤波器，因为近似误差在通带和阻带上都是均匀分布的。
  等同纹波法通常都是采用Park-McClellan迭代方法来实现的，与直接频率法相比，等同纹波设计法的优点在于通频带和抑制带偏差可以分别指定，且实现相同指标的滤波器时所用的滤波器阶数较小。

3.借助Matlab设计FIR滤波器

  在Matlab的SIGNAL PROCESSING TOOLBOX中有一个专门的数字滤波器设计软件模块FDA (Filter Design&Analysis Tool)，其功能强大，可以设计多种滤波器，而可以采用多种方法设计FIR滤波器，包括窗函数法和等同纹波法，它使用起来非常直观有效，在输入设计要求和设计方法选择后，计算出各阶系数，并以图形的直观方式显示幅频、相频、冲击响应和零极点图。它还可以把各阶系数以二进制补码的形式导出到文本文件中去，方便了系数的转换。

---

---

1.2 FPGA的硬件电路设计方法

  基于FPGA来设计电路与传统的方法有本质的不同，它摒弃了传统设计中的不灵活性，其可以通过软件编程的方法而对其硬件结构和工作方式进行重构，使得硬件的设计可以如同软件设计那样方便快捷，从这一点上来说，软件设计师只要具备一定的电子设计思想，就完全可以转到此项工作。
  FPGA这一切极大地改变了传统的数字硬件电路系统设计方法、设计过程、乃至设计观念。随着FPGA的不断发展，自身功能的不断完善和计算机辅助设计技术的提高，在现代电子系统设计领域中的电子设计自动化(EDA)便应运而生了，而电子设计自动化的关键技术之一就是采用硬件描述语言(VHDL)来设计数字硬件系统。这样，传统的数字硬件电路设计模式，就将被人们慢慢地淘汰，而可编程逻辑器件的使用将给电子电路的设计带来新的活力[7]。
  EDA自上而下的设计方法具有如下的特点[8]:

• 1.设计人员可自行设计所需的功能模块，使电路设计更趋合理，其体积功耗也可大为缩减;

• 2.用系统早期仿真可以发现设计中存在的问题，可大大缩短设计周期，降低费用;

• 3.降低了硬件电路设计难度，避免了很多繁杂的工作;

• 4.要设计文件是用VHDL语言编写的源文件，资料量小，便于保存，可继承性好且阅读方便。

  从上面的对比可以看出，采用FPGA设计硬件电路存在极大的优越性，省时、省力、节约成本、灵活性好且可移植性好。

---

参考文献

[1]罗耀国，娄淑琴.基于FPGA的字串行FIR滤波器的实现[J] .2005,12 (6 ):48-51
[2]彭文钦、孙世新.FIR滤波器分块并行算法分析[J].计算机应用，2006,20(3):32-35
[3]殷福亮，宋爱军.数字信号处理C语言程序集[M].沈阳:辽宁科学技术出版社，1997
[4]仲巡.FIR的FPGA设计[J].电子产品设计，2007, (2 ): 32-34
[5]褚振勇，屈丹，门向生.利用FPGA实现数字信号处理[J].电讯技术，2006,(1):91-96
[6]张卫杰，吴琼之.新一代CPLD及其应用[J].电子技术应用，2006, (7):63-66
[7]刘辉，杜兴民，李红军.宽带奈奎特FIR滤波器的设计与实现[J].电视技术，2005(1): 77-80
[8]黄正谨，徐坚，章小丽等.CPLD系统设计技术入门与应用[M].北京:电子工业出版社，2004
[9]褚振勇，翁木云.FPGA设计及应用[M].西安:电子科技大学出版社，2006
[10]李国峰，吴岳，秦世才.基于VHDL语言的LMS自适应滤波器的硬件实现方法[J]，南开大学学报(自然科学)，2006, 35 (3): 82-86
[11]、张维良，郭兴波，潘长勇等.高速FIR滤波器的流水线结构[J].电视技术，2005, (2 ): 57-60
[12]潘松、黄继业、王国栋.现代DSP技术[M].西安:电子科技大学出版社，2005
[13]刘刚，林志远.毅增.基于流水线技术的并行高效FIR滤波器设计[J].通讯与电视，2006, (7): 60-62
[14]付文武，周依林.基于高速流水线乘加器的fir滤波器设计[J].电子设计应用，2006, (9): 18-20
[[15]徐锋、禹卫东、唐红等.基于FPGA流水线分布式算法的FIR滤波器的实现[T].电子技术应用，2004, 7:70-73
[16]S.He，M.Torkelson.FPGA implementation of FIR filters using pipelined bit-serial canonical signed digit multipliers[J].IEEE 1994 custom integrated circuits conference，pp. 81-84
[17]Q.Zhao and Y.Tadokoro.A simple design of fir filters with powers-of-two coefficients [J].IEEE Trans.Circuits and systems，Vo .35，Nay 2005，pp .566一570.
[18]Henry Samueli.An improved search algorithm for the design of multiplierless fir filters with powers-of-two coefficients[J].IEEE Transactions on Circuits and systems，Vol. 36，No .7，July 1998.

---

---

---

---