FIR数字滤波器的FPGA实现(三)-并行FIR滤波器设计

(三)FIR数字滤波器的FPGA实现-并行FIR滤波器设计

---

---

  对于FIR滤波器主要涉及到滤波器的设计和滤波器的实现，设计和实现的区别如下图所示：

  实现是 forward problem，设计是 inverse problem

               What are inverse problems?

  本文主要涉及到FIR滤波器的实现，在实现的过程中，h[k]都是已知的，而h[k]的求解一般是设计的过程。具体内容包括，FIR滤波器的基本原理，串行FIR滤波器设计（此设计为滤波器实现的“设计”和FIR滤波器的设计不同，自行理会），并行FIR滤波器设计，串并FIR滤波器设计，分布式FIR滤波器设计，快速卷积型 FIR 滤波器、多通道 FIR 滤波器、多频响 FIR 滤波器。对于快速卷积型 FIR 滤波器、多通道 FIR 滤波器、多频响 FIR 滤波器会简单介绍，其中串行、并行、串并、分布式FIR滤波器设计会给出相应源码和仿真模型，如果条件允许会抽出一个源码在FPGA上运行，并进行实验分析。

---

0 并行FIR滤波器基本原理

  在某些场合， FIR 滤波器的釆样率很高， 实时性很强， 这就要求系统具有很高的处理速度和很大的数据吞吐率， 全并行结构就满足了这一要求。 它使得采样率与系统处理速度相等。 其思想是将一次滤波运算内的乘法同时执行， 最终达到“以资源换速度” 的目的。 全并行结构可采用直接型、 转置型、 脉动方式实现， 本节将重点讨论这几种实现方式。

---

1 基于直接型结构的全并行 FIR 滤波器

  不失一般性， 仍以 4 抽头为例， 对图 4.2所示的采用加法树的直接型结构使用流水线技术进行处理以缩短关键路径， 得到如图 4.24所示的结构。 这种结构是将一次滤波运算的所有乘法同时执行。图 4.24 中， 一次滤波运算所需要的输入数据依时间顺序沿寄存器链流动， 流动速率即为采样率， 也就是系统时钟频率， 可理解为输入数据缓存在寄存器中。

  完整Verilog代码如下:

`timescale 1ns / 1ps

module X_Parallel_FIR_Verilog
(
	input rst,                    //复位信号，高电平有效
	input clk,                    //FPGA系统时钟，频率为2kHz
	input signed [11:0] Xin,      //数据输入频率为2khZ
	output signed [28:0]Yout      //滤波后的输出数据
);
	
	//将数据存入移位寄存器Xin_Reg中
	reg signed[11:0] Xin_Reg[15:0];
	reg [3:0] i,j; 
	always @(posedge clk or posedge rst)
		if (rst)
			//初始化寄存器值为0
			begin 
				for (i=0; i<15; i=i+1)
					Xin_Reg[i]=12'd0;
			end
		else
			begin
			   //与串行结构不同，此处不需要判断计数器状态
				for (j=0; j<15; j=j+1)
					Xin_Reg[j+1] <= Xin_Reg[j];
				Xin_Reg[0] <= Xin;
			end
			
	//将对称系数的输入数据相加，同时将对应的滤波器系数送入乘法器
	//为了进一步提高运行速度，另外增加了一级寄存器
	reg signed [12:0] Add_Reg[7:0];
	always @(posedge clk or posedge rst)
		if (rst)
			//初始化寄存器值为0
			begin 
				for (i=0; i<8; i=i+1)
					Add_Reg[i]=13'd0;
			end
		else
			begin
				for (i=0; i<8; i=i+1)
					Add_Reg[i]={Xin_Reg[i][11],Xin_Reg[i]} + {Xin_Reg[15-i][11],Xin_Reg[15-i]};
			end

	//与串行结构不同，另外需要实例化8个乘法器IP核
	//实例化有符号数乘法器IP核mult
   wire signed [11:0] coe[7:0] ;   //滤波器为12比特量化数据
	wire signed [24:0] Mout[7:0];   //乘法器输出为25比特数据
	assign coe[0]=12'h000;
	assign coe[1]=12'hffd;
	assign coe[2]=12'h00f; 
	assign coe[3]=12'h02e;	
	assign coe[4]=12'hf8b;
	assign coe[5]=12'hef9; 	
	assign coe[6]=12'h24e;
	assign coe[7]=12'h7ff; 
	mult_gen_0	Umult0 (
		.CLK (clk),
		.A (coe[0]),
		.B (Add_Reg[0]),
		.P (Mout[0]));			
	mult_gen_0	Umult1 (
		.CLK (clk),
		.A (coe[1]),
		.B (Add_Reg[1]),
		.P (Mout[1]));		
	mult_gen_0	Umult2 (
		.CLK (clk),
		.A (coe[2]),
		.B (Add_Reg[2]),
		.P (Mout[2]));		
	mult_gen_0	Umult3 (
		.CLK (clk),
		.A (coe[3]),
		.B (Add_Reg[3]),
		.P (Mout[3]));		
	mult_gen_0	Umult4 (
		.CLK (clk),
		.A (coe[4]),
		.B (Add_Reg[4]),
		.P (Mout[4]));		
	mult_gen_0	Umult5 (
		.CLK (clk),
		.A (coe[5]),
		.B (Add_Reg[5]),
		.P (Mout[5]));		
	mult_gen_0	Umult6 (
		.CLK (clk),
		.A (coe[6]),
		.B (Add_Reg[6]),
		.P (Mout[6]));				
	mult_gen_0	Umult7 (
		.CLK (clk),
		.A (coe[7]),
		.B (Add_Reg[7]),
		.P (Mout[7]));

		
	//对滤波器系数与输入数据的乘法结果进行累加，并输出滤波后的数据
	//与串行结构不同，此处在一个时钟周期内直接将所有乘法器结果相加
	reg signed [28:0] sum;
	reg signed [28:0] yout;
	reg [3:0] k;
	always @(posedge clk or posedge rst)
		if (rst)
			begin 
				sum = 29'd0; 
				yout <= 29'd0;
			end
		else
			begin
			   yout <= sum;
				sum = 29'd0;
				for (k=0; k<8; k=k+1)
					sum = sum+Mout[k];
			end
	assign Yout = yout;
			
endmodule

  输出信号的29bit位宽是全分辨率输出，没有截位。“并行”FIR指的是多个乘法器并行地进行滤波器系数与输入数据之间的乘法计算，因此代码中我们需要缓存16个数据：

reg signed[11:0] Xin_Reg[15:0];   //[11:0]指单数据12bit位宽；[15:0]指共有16个数据
reg [3:0] i,j; 
always @(posedge clk or posedge rst)
    if (rst)
        //初始化寄存器值为0
        begin 
            for (i=0; i<15; i=i+1)
                Xin_Reg[i]=12'd0;
        end
    else
        begin
            for (j=0; j<15; j=j+1)  //每个时钟移位一个数据
                Xin_Reg[j+1] <= Xin_Reg[j];
            Xin_Reg[0] <= Xin;
        end

  由FIR系数的对称性可知，16个系数只需要8个乘法器即可，因此应该将对称系数多对应的输入数据相加：

reg signed [12:0] Add_Reg[7:0];
always @(posedge clk or posedge rst)
    if (rst)
        //初始化寄存器值为0
        begin 
            for (i=0; i<8; i=i+1)
                Add_Reg[i]=13'd0;
        end
    else
        begin
            for (i=0; i<8; i=i+1)   //对称系数相加
            Add_Reg[i]={Xin_Reg[i][11],Xin_Reg[i]}+{Xin_Reg[15-i][11],Xin_Reg[15-i]};
        end

  由于加法会增加一个bit位宽，因此相加结构扩充为13bit。由于输入数据为二进制补码带符号数，因此在相加前需要先使用Verilog中的拼接运算符{}扩展符号位到最高位。接下来例化8个乘法器IP核进行乘法运算：

wire signed [11:0] coe[7:0] ;    //滤波器为12比特量化数据
    wire signed [24:0] Mout[7:0];   //乘法器输出为25比特数据
    assign coe[0]=12'h000;
    assign coe[1]=12'hffd;
    assign coe[2]=12'h00f; 
    assign coe[3]=12'h02e;  
    assign coe[4]=12'hf8b;
    assign coe[5]=12'hef9;  
    assign coe[6]=12'h24e;
    assign coe[7]=12'h7ff; 
    mult_gen_0  Umult0 (
        .CLK (clk),
        .A (coe[0]),
        .B (Add_Reg[0]),
        .P (Mout[0]));          
    mult_gen_0  Umult1 (
        .CLK (clk),
        .A (coe[1]),
        .B (Add_Reg[1]),
        .P (Mout[1]));      
    mult_gen_0  Umult2 (
        .CLK (clk),
        .A (coe[2]),
        .B (Add_Reg[2]),
        .P (Mout[2]));      
    mult_gen_0  Umult3 (
        .CLK (clk),
        .A (coe[3]),
        .B (Add_Reg[3]),
        .P (Mout[3]));      
    mult_gen_0  Umult4 (
        .CLK (clk),
        .A (coe[4]),
        .B (Add_Reg[4]),
        .P (Mout[4]));      
    mult_gen_0  Umult5 (
        .CLK (clk),
        .A (coe[5]),
        .B (Add_Reg[5]),
        .P (Mout[5]));      
    mult_gen_0  Umult6 (
        .CLK (clk),
        .A (coe[6]),
        .B (Add_Reg[6]),
        .P (Mout[6]));              
    mult_gen_0  Umult7 (
        .CLK (clk),
        .A (coe[7]),
        .B (Add_Reg[7]),
        .P (Mout[7]));

  12bit的滤波器系数与13bit的输入信号数据相乘结果为25bit。乘法结果累加即为滤波器的输出结果：

reg signed [28:0] sum;
reg signed [28:0] yout;
reg [3:0] k;
always @(posedge clk or posedge rst)
if (rst)
begin
sum = 29’d0;
yout <= 29’d0;
end
else
begin
yout <= sum;
sum = 29’d0;
for (k=0; k<8; k=k+1)
sum = sum+Mout[k]; //相加输出结果
end
assign Yout = yout;

  8个25bit的数相加，结果可能扩展到29bit，这也是全分辨率输出的结果。可以看到并行结构的FIR乘法、加法运算都是在一个时钟内完成，因此每个时钟都能获得一个输出。

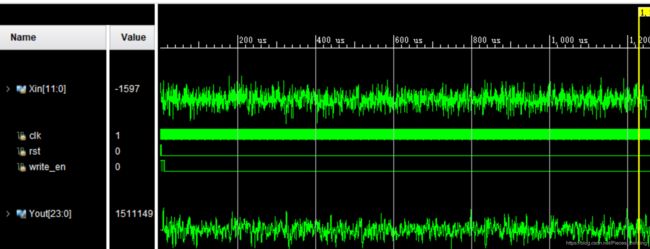
  使用MATLAB生成一个200khz+800kHz的混合频率信号，写入txt文件，再生成一个噪声信号写入txt文件。

  对正弦信号的滤波如下图所示：

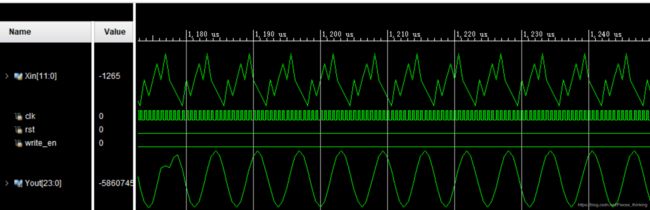
  明显看到经过500kHz低通滤波器滤波后，输入的200+800kHz信号只剩下200kHz的频率分量。

  对噪声信号的滤波如下图所示：

---

2 基于转置型结构的全并行 FIR 滤波器

  对图 4.7 所示的转置型结构使用流水线技术进行处理得到如图 4.25 所示的 4 抽头全并行FIR 滤波器硬件结构。 这种结构是将不同滤波运算的相关乘法同时执行， 如图 4.26 所示。 图中同一条虚线上的乘法同时执行。

  转置型结构 FIR 滤波器采用 Matlab 描述如 Matlab 代码 4-2 所示， 输出 y 可通过 yref 对比验证。

  图 4.25 中， 输入数据同时传送到每个乘法器的输入端与相应的系数相乘。 此时， 系数的排列顺序由左至右与直接型结构恰好相反。 设计中采用了加法链的结构， 这使得每个乘加单元（ 图中的虚线框） 非常易于映射为 Xilinx 7 系列 FPGA 中的 DSP48E1, 第一个乘加单元工作模式为 AxB+C, 并将 C 设置为 0, 其余乘加单元工作模式为 AxB+PCIN, 配置形式如图 4.27 所示， PCIN 用于两个 DSP48E1 的级联。
  转置型结构具有这样的特点， 即输入数据同时与 N 个固定数相乘， 这里的固定数即为滤波器系数。 于是， 可构造一个乘法模块完成此功能， 如图 4.28 所示。 从而， 设计的关键就是设计此乘法模块。 与固定数相乘的乘法器可根据固定数的特点通过移位、 相加的手段实现， 进而节省了硬线乘法器 DSP48E1 ) 资源。

  假定滤波器系数为 h(3)= 13 , h(2)= 3 , h(1) = 27 , h(0) = 37，那么可通过图 4.29 所示的移位、 相加运算实现乘法。 这正是转置结构的优势所在。

  图 4.29 中， “<

---

3 基于脉动结构的全并行 FIR 滤波器

  脉动结构 （ 又称脉动阵列， Systolic ) 是一种并行流水实现高速信号处理和数据处理的硬件实现方式， 由 H.T.Kung 首先提出。 它具有模块化、 规则化、 链接的局部性和高度流水等一系列优点。 脉动结构处理器（ 又称处理单元 Process Element, PE ) 是一个多处理器结构， 所有的处理器都有节奏地同步工作， 并使被处理数据通过系统。 这个操作类似心脏的血液流动， 因此命名为“ 脉动” 。
  4 抽头脉动 FIR 滤波器的硬件结构如图 4.30 所示。 图中， 每个虚线框即为一个处理单元PE 输入数据通过级联的寄存器流动到每个 PE 与相应的滤波器系数相乘， 乘积累加的部分和同样沿底部的寄存器链移动。 与转置结构不同的是此时滤波器系数的排列顺序由左至右为h(0)〜 h(3)。 除 PE1 外， 其余每个处理单元输入端均为两级寄存， 目的是保证数据对齐， 补偿输入数据之间的固有延时（ 如 x(l)相对于 x(0)有 1 个时钟周期的延时） 以及加法输出的延时。 假定当输入端 din 为 x(3)时， 节点 A 输出 x(2) ，x(3)h(0)到 PE2 中加法器的输入端节P1 需要 3 个时钟周期， 那么 x(2)h(1) 到加法器的另一个输入端节点 P2 也必须保持 3 个时钟周期， 才能保证数据正确的时间相加。 这种结构也是将不同滤波运算的相关乘法同时执行，如图 4.31 所示。 图中同一条虚线上的乘法同时执行。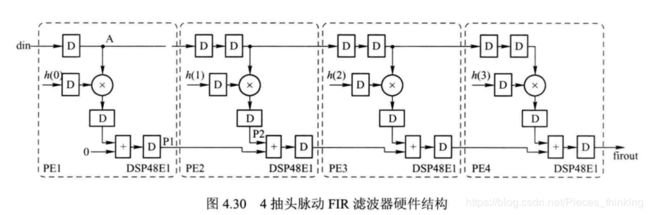

  图 4.30 中， 每个 PE 都可用 Xilinx 7 系列 FPGA 中的 DSP48E1 实现。 将 DSP48E1 配置为 AxB+C 并将 C 设置为 0 即为 PE1 , 配置为AxB+PCIN 并将 B 端口输入数据延时两个时钟周期由 BCOUT 输出用作级联即为 PE2〜PE4 如图 4.32 所示。

---

4 系数对称的全并行 FIR 滤波器的设计

  对于系数对称的 FIR 滤波器， 可利用其对称性通过预加减少处理单元的个数。 以 8 抽头偶对称为例， 其系数满足式（4.25 )。 从而， 在 XilinxVirtex-5 中相应的硬件结构如图 4.33 所示。 显然， 处理单元的个数可减少至 4 个。 此时， PE1 对 应 的 DSP48E 配置为 AxB+C，PE2〜PE4 对应的 DSP48E 配置为 AxB+PCIN 由于 Virtex-5 中的 DSP48E 没有预加器， 因此需要额外的逻辑资源实现预加功能。 在 Virtex-6 和 7 系 列 FPGA 中 的 DSP48E1 本身就带有预加器，因此，图 4.33 所示结构可进一步优化， 如图 4.34 所示。

---

---

---