K均值算法(K-means)聚类
主要知识点
- K-means算法
- KMeans(n_clusters=3)
- K-means的中心点
- centers = kmeans.cluster_centers_
- 坐标轴中文显示问题
- 坐标轴字体、负号还原问题
3D绘图
- from mpl_toolkits.mplot3d import Axes3D
- 建立坐标系
- ax = plt.subplot(projection=’3d’)
make_blobs生成有中心点的数据
centers=3 中心点
cluster_std =[0.5, 2, 10] 标准差
一、K-means算法原理
1)概念
一种无监督的学习,事先不知道类别,自动将相似的对象归到同一个簇中。
K-Means算法是一种聚类分析(cluster analysis)的算法,其主要是来计算数据聚集的算法,主要通过不断地取离种子点最近均值的算法。
K-Means算法主要解决的问题如下图所示。我们可以看到,在图的左边有一些点,我们用肉眼可以看出来有四个点群,但是我们怎么通过计算机程序找出这几个点群来呢?于是就出现了我们的K-Means算法
2)算法示例
从上图中,我们可以看到,A,B,C,D,E是五个在图中点。而灰色的点是我们的种子点,也就是我们用来找点群的点。有两个种子点,所以K=2。
然后,K-Means的算法如下:
随机在图中取K(这里K=2)个种子点。
然后对图中的所有点求到这K个种子点的距离,假如点Pi离种子点Si最近,那么Pi属于Si点群。(上图中,我们可以看到A,B属于上面的种子点,C,D,E属于下面中部的种子点)
接下来,我们要移动种子点到属于他的“点群”的中心。(见图上的第三步)
然后重复第2)和第3)步,直到,种子点没有移动(我们可以看到图中的第四步上面的种子点聚合了A,B,C,下面的种子点聚合了D,E)。
这个算法很简单,重点说一下“求点群中心的算法”:欧氏距离(Euclidean Distance):差的平方和的平方根

K-Means主要最重大的缺陷——都和初始值有关:
K是事先给定的,这个K值的选定是非常难以估计的。很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适。(ISODATA算法通过类的自动合并和分裂,得到较为合理的类型数目K)
K-Means算法需要用初始随机种子点来搞,这个随机种子点太重要,不同的随机种子点会有得到完全不同的结果。(K-Means++算法可以用来解决这个问题,其可以有效地选择初始点)
3)K-Means算法步骤
- 从数据中选择k个对象作为初始聚类中心;
- 计算每个聚类对象到聚类中心的距离来划分;
- 再次计算每个聚类中心
- 计算标准测度函数,直到达到最大迭代次数,则停止,否则,继续操作。
- 确定最优的聚类中心
4)K-Means算法应用
看到这里,你会说,K-Means算法看来很简单,而且好像就是在玩坐标点,没什么真实用处。而且,这个算法缺陷很多,还不如人工呢。是的,前面的例子只是玩二维坐标点,的确没什么意思。但是你想一下下面的几个问题:
1)如果不是二维的,是多维的,如5维的,那么,就只能用计算机来计算了。
2)二维坐标点的X,Y 坐标,其实是一种向量,是一种数学抽象。现实世界中很多属性是可以抽象成向量的,比如,我们的年龄,我们的喜好,我们的商品,等等,能抽象成向量的目的就是可以让计算机知道某两个属性间的距离。如:我们认为,18岁的人离24岁的人的距离要比离12岁的距离要近,鞋子这个商品离衣服这个商品的距离要比电脑要近,等等。
4)常见问题
- k值不合适
- 数据有偏差
- 样本数量差别很大
- 数据标准差差别很大
5)解决方法
K值太重要了
K-Means++算法
原理就是将K的值 ++ 一个一个试K的值
二、聚类实例
from sklearn.cluster import KMeans
1)使用make_blobs生成数据
导包
from sklearn.datasets import make_blobs#参数:
# n_samples=100 样本数量
# n_features=2 特征数量
# centers=3 中心点
#返回值:
# X_train: 测试集
# y_train: 特征值
X_train,y_train = make_blobs(n_samples=100, n_features=2, centers=3)将生成的数据绘制出来
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)2)建立模型并训练
#参数
# n_clusters 将预测结果分为几簇
kmeans = KMeans(n_clusters=3) # 获取模型
kmeans.fit(X_train) #这里不需要给他答案 只把要分类的数据给他 即可3)使用相同的数据进行预测
y_ = kmeans.predict(X_train)4)原数据特征值与预测结果比较
plt.scatter(X_train[:,0],X_train[:,1],c=y_train) # 预测结果
plt.scatter(X_train[:,0],X_train[:,1],c=y_) #原结果三、足球数据预测
使用K-Means进行数据处理,对亚洲球队进行分组,分三组
绘制3D图形
1)导包
from mpl_toolkits.mplot3d import Axes3D2)获取数据
列名修改为:”国家”,”2006世界杯”,”2010世界杯”,”2007亚洲杯”
df = pd.read_csv('./data/AsiaFootball.csv',header=None)
df.columns = ["国家","2006世界杯","2010世界杯","2007亚洲杯"]提取训练数据,将国家名去掉
data = df.iloc[:,1:] # 所有行都要 从1开始 到最后 (如果是取到最后 冒号后面的可以省略)
data3)建立模型并训练
kmeans = KMeans(n_clusters=3)
kmeans.fit(data) #这里训练数据只传入训练数据,不用传入结果集4)预测结果
1、训练后用模型预测
kmeans.predict(data)2、训练并直接预测
和上面的效果一样
y_ = kmeans.fit_predict(data)5)直观查看分好组的国家
df[y_==0]['国家']
1 日本
2 韩国
Name: 国家, dtype: objectdf[y_==1]['国家']
0 中国
5 伊拉克
6 卡塔尔
7 阿联酋
9 泰国
10 越南
11 阿曼
14 印尼
Name: 国家, dtype: objectdf[y_==2]['国家']
3 伊朗
4 沙特
8 乌兹别克斯坦
12 巴林
13 朝鲜
Name: 国家, dtype: object6)for循环打印出分为三类的国家
for i in range(3):
s = df[y_==i]['国家']
for country in s:
print(country)
print('\n')
日本
韩国
中国
伊拉克
卡塔尔
阿联酋
泰国
越南
阿曼
印尼
伊朗
沙特
乌兹别克斯坦
巴林
朝鲜7)绘制三维立体图形
1、导包
from mpl_toolkits.mplot3d import Axes3D2、建立坐标系
ax = plt.subplot(projection='3d')3、画出坐标数据
坐标轴中文显示问题
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] #中文显示问题坐标轴字体还原问题
坐标轴负号还原问题
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['STXINWEI'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题画出坐标点,并设置坐标轴数据
plt.figure(figsize=(12,8))
ax = plt.subplot(projection='3d')
x = df['2006世界杯']
y = df['2010世界杯']
z = df['2007亚洲杯']
ax.scatter3D(x,y,z,c=y_,s=100,alpha=1)
ax.set_xlabel('2006世界杯')
ax.set_ylabel('2010世界杯')
ax.set_zlabel('2007亚洲杯')8)K-means的中心点
centers = kmeans.cluster_centers_
centers
array([[22.5, 12. , 3.5],
[50. , 47.5, 7.5],
[34.6, 38.4, 7.6]])9)将分类的中心点也画到图上
plt.figure(figsize=(12,8))
ax = plt.subplot(projection='3d')
x = df['2006世界杯']
y = df['2010世界杯']
z = df['2007亚洲杯']
ax.scatter3D(x,y,z,c=y_,s=100,alpha=1)
ax.set_xlabel('2006世界杯')
ax.set_ylabel('2010世界杯')
ax.set_zlabel('2007亚洲杯')
ax.scatter3D(centers[:,0],centers[:,1],centers[:,2],c='r')四、聚类实践与常见错误
1)使用make_blobs创建样本点
# 样本量 n_samples=100
# 特征量 n_features=2
# 中心点 centers=3
X_train,y_train = make_blobs(n_samples=1500, n_features=2, centers=3)2)第一种错误,k值不合适,make_blobs默认中心点三个
1、创建训练集并绘图
X_train,y_train = make_blobs(n_samples=1500, n_features=2, centers=3)画图查看绘制的点
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)2、预测结果并绘图
kmeans = KMeans(n_clusters=4)
y_ = kmeans.fit_predict(X_train) #这里预测有4个中心点
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)3)第二种错误:标准差cluster_std不相同
1、创建训练集并绘图
#参数
# cluster_std 各个中心的标准差
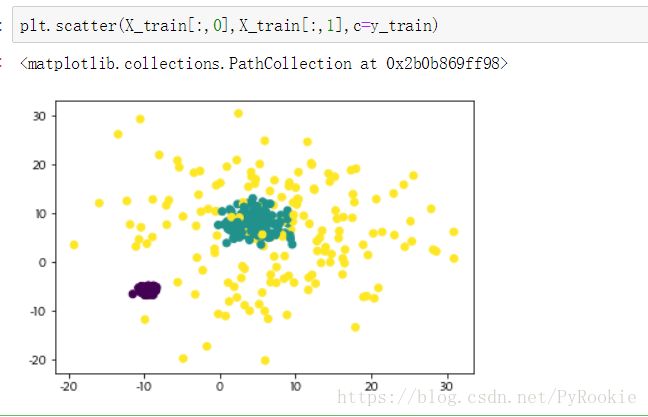
X_train,y_train = make_blobs(n_samples=500, n_features=2, centers=3, cluster_std=[0.5,2,10]) 绘制训练集
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)2、预测结果并绘图
kmeans = KMeans(n_clusters=3)
y_ = kmeans.fit_predict(X_train)
plt.scatter(X_train[:,0],X_train[:,1],c=y_)4)第三种错误,数据有偏差
1、让样本产生偏差
使用点乘使样本产生偏差
test = [
[1,2],
[3,4],
[5,6]
]
trans = [
[0.6,-0.6],
[-0.4,0.8]
]
np.dot(test,trans)
array([[-0.2, 1. ],
[ 0.2, 1.4],
[ 0.6, 1.8]])可以看出 得到的数据与原数据相比缩小了
2、对产生的数据造成偏差
trans = [
[0.6,-0.6],
[-0.4,0.8]
]
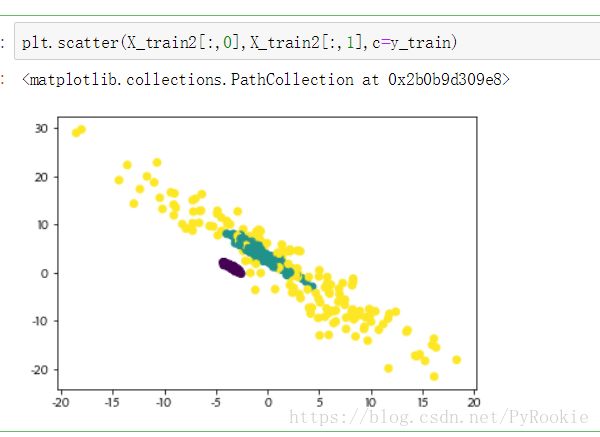
X_train2 = np.dot(X_train,trans)绘制出偏差后的数据
3、对偏差数据进行训练预测
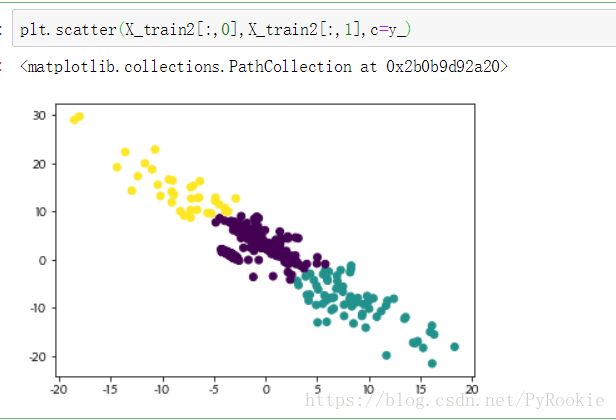
kmeans = KMeans(n_clusters=3)
y_ = kmeans.fit_predict(X_train2)
plt.scatter(X_train2[:,0],X_train2[:,1],c=y_)5)第四个错误:样本数量不同
1、创建数据集
X,y = make_blobs(n_samples=1500, n_features=2, centers=3)2、数据处理
将分make_blobs好的数据各取不等份样本,组成一组新的数据集
# 创建训练集
X1 = X[y==0] # X1中的这些点 目标值都是0
X2 = X[y==1][:100] # X2中的这些点 目标值都是1
X3 = X[y==2][:10] # X3中的这些点 目标值都是2
# 将三个合为一个训练集
X = np.concatenate((X1,X2,X3))创建结果集
# 前500个为0 再来100个1 再来10个2
y_train = [0]*500+[1]*100+[2]*10绘制创建出来的点
plt.scatter(X[:,0],X[:,1],c=y_train)3、使用模型训练并预测
kmeans = KMeans(n_clusters=3)
y_ = kmeans.fit_predict(X)
# 绘图比较与原数据的差异
plt.scatter(X[:,0],X[:,1],c=y_)