遗传算法-实验 Hexagonal tortoise problem (Using C language)

@ 初步算法，有待完善，仅供参考，转载请附原文链接。

遗传算法：龟纹图问题

1、Introduction

Jisuwimundo is a hexagonal tortoise problem designed by Chosun scholar Choi Seok-jeong. The tortoise is a shape in which hexagons are interlocked with each other. There is a condition that a ruler is placed so that the sum of the corner numbers of the hexagons is equal. In the case of an exponential return figure with a number of N, numbers from 1 to N are placed. The objective of the problem is that the exponential return problem is an algorithm that cannot be solved within polynomial (NP-hard). Therefore, there are effective genetic algorithms that search for limited space.

The characteristics of hexagonal tortoise problem:
1） Parameters for each corner of the hexagon;
2) The sum of each hexagon is equal.

The Figure 1.1 is the 3 × 3 hexagon tortoise.

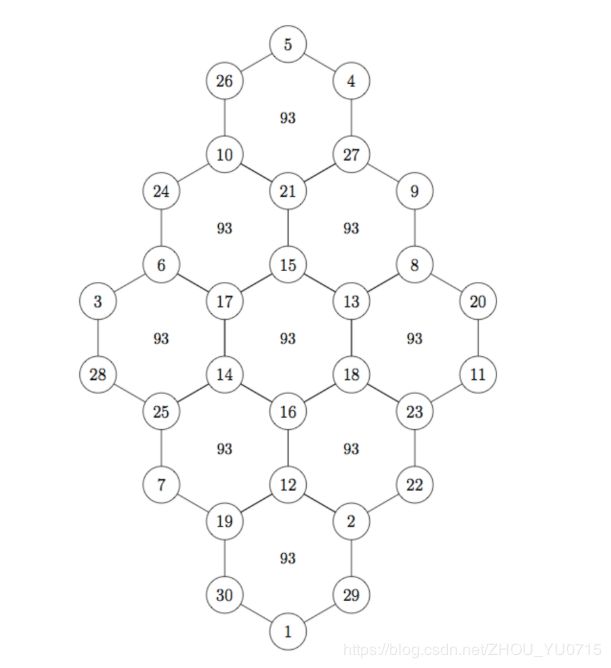
2、project process

a) System structure

Since this problem is NP-hard, it is solved using genetic algorithms. The overall system architecture is shown in Figure 2.1. First, create the population, then calculate the fitness, select the parents in the population, cross between the selected parents, and ensure the diversity of the population through mutation and substitution. Finally, the judgment is made by the termination condition. If the condition is met, it is terminated and output. If it is not met, the fitness assessment is repeated until the result appears.

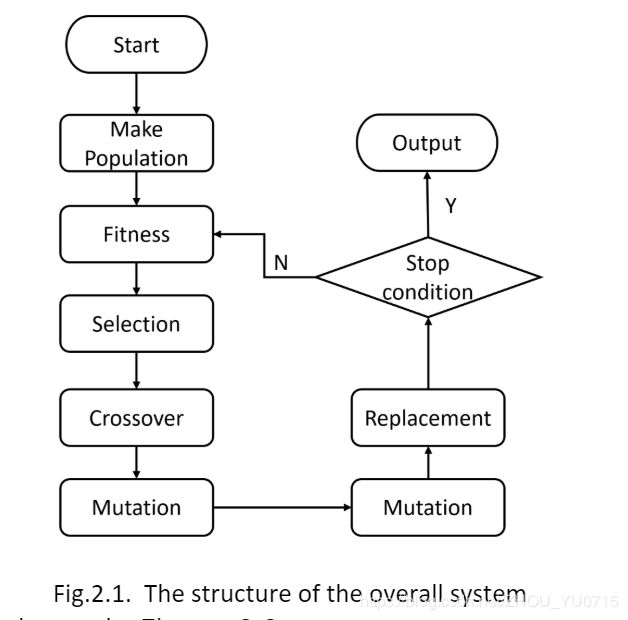
This part of coding is shown in thiss:

int main(void)
{
	int seed;
	int i, j;

	seed = time(NULL);
	srand(seed);

	MakePopulation(valuesOfParents);
//	Show(valuesOfParents);
	Fitness();

	for(i = 0; i < 10000000; i++)
	{
		for(j = 0; j < CHILDRENNUM; j++)
		{
			parentOne = Selection();
			parentTwo = Selection();

			valuesOfChildren = pmxCrossOver(parentOne, parentTwo);

			valuesOfChildren.parent1 = parentOne;
			valuesOfChildren.parent2 = parentTwo;

			valuesOfChildren = MakeSixAngle(valuesOfChildren);
			valuesOfChildren = Mutation(valuesOfChildren);
			valuesOfChildren = MakeSixAngle(valuesOfChildren);

			children[j] = valuesOfChildren;
		}
		Replacement();
		Fitness();

		count++;
		Show(valuesOfChildren);
		if(valuesOfChildren.dispersion == 0)
		{
			printf("\n finished!  \n");
			ResultShow(valuesOfChildren);
			break;
		}
	}
	return 0;
}

b) Representation

In the implementation of the genetic algorithm, the first problem is to code the problem reasonably. Translate into digital problems. Here, a locus-based encoding method is adopted. This method is shown in the Figure 2.3.

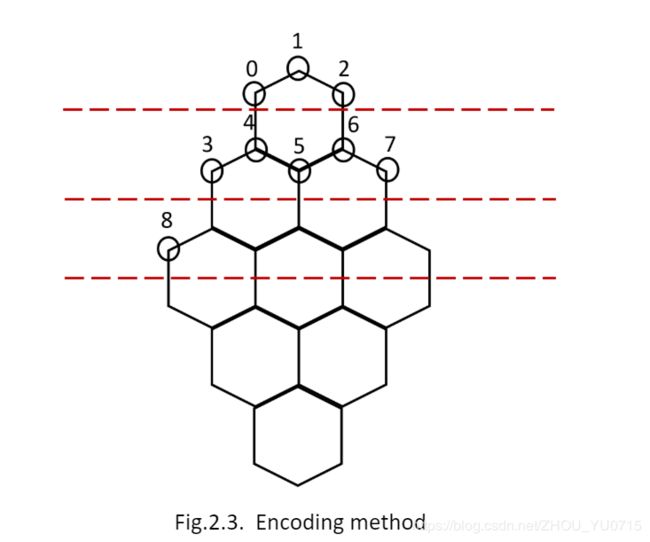
This part of conding is shown:

//*********制造出不同的数字*****************//

turtle MakeNumber(void)
{
	int i, j;
	for(i = 0; i < NODENUM; i++)
	{
		valuesOfParents.nodes[i] = rand()%NODENUM + 1;	//产生0~nodenum个随机整数
		for(j = 0; j < i; j++)
		{	
			//*************是的所有节点具有不同的值*******************//
			if(valuesOfParents.nodes[i] == valuesOfParents.nodes[j])
			{
				valuesOfParents.nodes[i] = rand()%NODENUM +1;
				j = -1;
			}
			//******************************************************//
		}
	}
	return valuesOfParents;
}

//***************Population number 给解编号**********************//

turtle MakePopulation(turtle valuesOfParents)
{
	int i;
	for(i = 0; i <PARENTNUM; i++)
	{
		valuesOfParents = MakeNumber();
		parents[i] = valuesOfParents;
	}
	return valuesOfParents;
}

c) Slection

Choose the right parents. There are also many ways to selection. The method used here is the roulette wheel selection. The K value is 4.

This part of coding is shown:

//*******************rullet wheel*****************//
int Selection(void)
{
   int i, s, point;
   if(sumOfFit == 0)
   	sumOfFit = 1;
   point = rand()%sumOfFit;

   s = 0;
   for(i = 0; i < PARENTNUM; i++)
   {
   	s += parents[i].fitness;
   	if(point << s)
   		return i;
   }
   return PARENTNUM-1;
}

d) Crossover

There are also many ways to crossover. The method used here is the PMX crossover. The method is shown in the Figure 2.6.

This part of coding is shown:

//**************PMXcrossover******************//
turtle pmxCrossOver(int parentOne, int parentTwo)
{
	int i, j;
	int firstCutPoint, secondCutPoint;

	firstCutPoint = rand()%(NODENUM);
	secondCutPoint = rand()%(NODENUM - firstCutPoint)+firstCutPoint;

	for(i = firstCutPoint; i < secondCutPoint; i++)
		valuesOfChildren.nodes[i] = parents[parentOne].nodes[i];

	for(i = secondCutPoint; i < NODENUM; i++)
	{
		valuesOfChildren.nodes[i] = parents[parentTwo].nodes[i];
		for(j = firstCutPoint; j < secondCutPoint; j++)
		{
			if(valuesOfChildren.nodes[j] == valuesOfChildren.nodes[i])
			{
				while(valuesOfChildren.nodes[j] == valuesOfChildren.nodes[i])
				{
					j = firstCutPoint-1;
					valuesOfChildren.nodes[i] = parents[parentTwo].nodes[i];
				}
			}
		}
	}

	for(i = 0; i < firstCutPoint; i++)
	{
		valuesOfChildren.nodes[i] = parents[parentTwo].nodes[i];
		for(j = firstCutPoint; j < NODENUM; j++)
		{
			if(valuesOfChildren.nodes[j] == valuesOfChildren.nodes[i])
			{
				while(valuesOfChildren.nodes[j] == valuesOfChildren.nodes[i])
				{
					j = firstCutPoint - 1;
					valuesOfChildren.nodes[i] = parents[parentTwo].nodes[j];
				}
			}
		}
	}
	return valuesOfChildren;
}

e) Mutation

In order to maintain the diversity of the population, the characteristics not introduced by the parents were introduced to improve the quality of the population. Mutation is usually selected, and the mutation rate in this project is set to 0.1.
This part of coding is shown:

//*********************mutation*******************//
turtle Mutation(turtle valuesOfChildren)
{
	int i, j;
	int temp;

	for(i = 0; i < NODENUM; i++)
	{
		if(rand()%100 < MUTATIONRATE)
		{
			j = rand()%NODENUM;
			temp = valuesOfChildren.nodes[i];
			valuesOfChildren.nodes[i] = valuesOfChildren.nodes[j];
			valuesOfChildren.nodes[j] = temp;
		}
	}
	return valuesOfChildren;
}

f) Replacement

Replacement is also one of the methods to ensure the diversity of the population. The replacement scheme used here is to replace the parent chromosome when the generated offspring fit is higher than the fit of one of the parents.
This part of coding is shown:

//*****************replacement**********************//
void Replacement(void)
{
	int i;

	for(i = 0; i < CHILDRENNUM; i++)
	{
		if(parents[children[i].parent2].primaryFit < children[i].primaryFit)
			parents[children[i].parent2] = children[i];
		else if(parents[children[i].parent1].primaryFit < children[i].primaryFit)
			parents[children[i].parent1] = children[i];
		else  parents[Worst] = children[i];
	}
}

g) Fitness

When setting fitness, the conditions used are hexagonal sums equal to each other, so the mean, variance, standard deviation, etc. are used to represent the dispersion of the current values. The final fitness is represented by the difference between the mean and the standard deviation. If it is equal to 0, it means equal. A larger value indicates a larger gap.

//***********************求和*************************//
turtle MakeSixAngle(turtle data)
{
//2*2

	data.SIXANGLE[0] = data.nodes[0] + data.nodes[1] + data.nodes[2] + data.nodes[4] + data.nodes[5] + data.nodes[6];
	data.SIXANGLE[1] = data.nodes[3] + data.nodes[4] + data.nodes[5] + data.nodes[8] + data.nodes[9] + data.nodes[10];
	data.SIXANGLE[2] = data.nodes[5] + data.nodes[6] + data.nodes[7] + data.nodes[10] + data.nodes[11] + data.nodes[12];
	data.SIXANGLE[3] = data.nodes[9] + data.nodes[10] + data.nodes[11] + data.nodes[13] + data.nodes[14] + data.nodes[15];
	//求平均值
	data.average = (data.SIXANGLE[0]+data.SIXANGLE[1]+data.SIXANGLE[2]+data.SIXANGLE[3])/SIXANGLENUM;													//2by2
	//求方差：与期望之间的差距
	data.dispersion =
			(
//2by2
			pow((double)data.SIXANGLE[0]-data.average,2)+pow((double)data.SIXANGLE[1]-data.average,2)
			+pow((double)data.SIXANGLE[2]-data.average,2)+pow((double)data.SIXANGLE[3]-data.average,2))/SIXANGLENUM;
//方差的平方：标准差
	data.deviation = sqrt(data.dispersion);

//初选
	data.primaryFit = data.average - data.deviation*sqrt((double)NODENUM);

	return data;
}

//*************fitness条件**********************//
void Fitness(void)
{
	int i;
	BestFitness = -100;
	WorstFitness = 100;
	sumOfPrimaryFit = 0;	//适应度

	for(i = 0; i < PARENTNUM; i++)
	{
		sumOfPrimaryFit += parents[i].primaryFit;

		if(BestFitness < parents[i].primaryFit)
		{
			BestFitness = parents[i].primaryFit;
			Best = i;
		}
		if(WorstFitness > parents[i].primaryFit)
		{
			WorstFitness = parents[i].primaryFit;
			Worst = i;
		}
	}

	sumOfFit = 0;

	for(i = 0; i < PARENTNUM; i++)
	{
		parents[i].fitness = (int)((SELECTION-1)*(parents[i].primaryFit - WorstFitness) 
									+ (BestFitness - WorstFitness));
		sumOfFit += parents[i].fitness;  //适度评分
	}
}

//*******************rullet wheel*****************//
int Selection(void)
{
	int i, s, point;
	if(sumOfFit == 0)
		sumOfFit = 1;
	point = rand()%sumOfFit;

	s = 0;
	for(i = 0; i < PARENTNUM; i++)
	{
		s += parents[i].fitness;
		if(point << s)
			return i;
	}
	return PARENTNUM-1;
}

3、Result

When the program runs, the result gradually converges, which proves that it can output the correct result.

[2 × 2 nodes = 16 hexagon = 4]

However, during the operation, it is found that the results do not appear once. For example, the situation of 4 hexagons will appear as shown in the Figure 3.2.

4、Conclusion

Through this experiment, I have a clearer understanding of the advantages of the genetic algorithm. I only need to consider the conditions for the final result. The algorithm will continue to check and calculate the final result. In this process, the programmer is not required to consider the functional relationship between the solution and the solution, which eases the process. At that time, the disadvantage was that the time charges were very large. At each run, the results are different and there is a certain gap, indicating that the algorithm sometimes converges too early, falls into a local optimal solution, and the stability is not very high. Larger. Therefore, it is necessary to optimize the algorithm, which is also the final part of the genetic algorithm.

附完整代码：

#include 
#include 
#include 	//time()
#include 
#define NODENUM 	16//96		//node number 节点数
#define SIXANGLENUM	4 //36		//mix number  六边形个数
#define PARENTNUM	500//500
#define CHILDRENNUM	20

#define MUTATIONRATE	1
#define SELECTION		4

typedef struct 
{
	int nodes[NODENUM];

	int SIXANGLE[SIXANGLENUM];
	int parent1, parent2;

	double average;			//平均值
	double dispersion;		//与期望之间的差距
	double deviation;		//标准差
	double primaryFit;		//初选
	int fitness;			//适应度
}turtle;


turtle valuesOfParents, valuesOfChildren;
turtle parents[PARENTNUM];
turtle children[CHILDRENNUM];


turtle MakeNumber(void);
turtle MakePopulation(turtle valuesOfParents);
turtle MakeSixAngle(turtle valuesOfParents);
int Selection(void);
turtle pmxCrossOver(int parentOne, int parentTwo);
turtle Mutation(turtle valuesOfChildren);
void Show(turtle valuesOfChildren);
void ResultShow(turtle valuesOfChildren);
void Replacement(void);
void Fitness(void);


int Best, Worst, count;
int parentOne, parentTwo;
double BestFitness, WorstFitness, sumOfPrimaryFit;
int sumOfFit;

int main(void)
{
	int seed;
	int i, j;

	seed = time(NULL);
	srand(seed);

	MakePopulation(valuesOfParents);
//	Show(valuesOfParents);
	Fitness();

	for(i = 0; i < 10000000; i++)
	{
		for(j = 0; j < CHILDRENNUM; j++)
		{
			parentOne = Selection();
			parentTwo = Selection();

			valuesOfChildren = pmxCrossOver(parentOne, parentTwo);

			valuesOfChildren.parent1 = parentOne;
			valuesOfChildren.parent2 = parentTwo;

			valuesOfChildren = MakeSixAngle(valuesOfChildren);
			valuesOfChildren = Mutation(valuesOfChildren);
			valuesOfChildren = MakeSixAngle(valuesOfChildren);

			children[j] = valuesOfChildren;
		}
		Replacement();
		Fitness();

		count++;
		Show(valuesOfChildren);
		if(valuesOfChildren.dispersion == 0)
		{
			printf("\n finished!  \n");
			ResultShow(valuesOfChildren);
			break;
		}
	}
	return 0;
}


//*********制造出不同的数字*****************//

turtle MakeNumber(void)
{
	int i, j;
	for(i = 0; i < NODENUM; i++)
	{
		valuesOfParents.nodes[i] = rand()%NODENUM + 1;	//产生0~nodenum个随机整数
		for(j = 0; j < i; j++)
		{	
			//*************是的所有节点具有不同的值*******************//
			if(valuesOfParents.nodes[i] == valuesOfParents.nodes[j])
			{
				valuesOfParents.nodes[i] = rand()%NODENUM +1;
				j = -1;
			}
			//******************************************************//
		}
	}
	return valuesOfParents;
}

//***************Population number 给解编号**********************//

turtle MakePopulation(turtle valuesOfParents)
{
	int i;
	for(i = 0; i <PARENTNUM; i++)
	{
		valuesOfParents = MakeNumber();
		parents[i] = valuesOfParents;
	}
	return valuesOfParents;
}

//***********************求和*************************//
turtle MakeSixAngle(turtle data)
{
//2*2

	data.SIXANGLE[0] = data.nodes[0] + data.nodes[1] + data.nodes[2] + data.nodes[4] + data.nodes[5] + data.nodes[6];
	data.SIXANGLE[1] = data.nodes[3] + data.nodes[4] + data.nodes[5] + data.nodes[8] + data.nodes[9] + data.nodes[10];
	data.SIXANGLE[2] = data.nodes[5] + data.nodes[6] + data.nodes[7] + data.nodes[10] + data.nodes[11] + data.nodes[12];
	data.SIXANGLE[3] = data.nodes[9] + data.nodes[10] + data.nodes[11] + data.nodes[13] + data.nodes[14] + data.nodes[15];
/*//3*3

	data.SIX[4] = data.nodes[8] + data.nodes[9] + data.nodes[13] + data.nodes[16] + data.nodes[18] + data.nodes[19];
	data.SIX[5] = data.nodes[11] + data.nodes[12] + data.nodes[17] + data.nodes[21] + data.nodes[20] + data.nodes[15];
	data.SIX[6] = data.nodes[13] + data.nodes[14] + data.nodes[24] + data.nodes[23] + data.nodes[22] + data.nodes[19];
	data.SIX[7] = data.nodes[14] + data.nodes[15] + data.nodes[20] + data.nodes[24] + data.nodes[25] + data.nodes[26];
	data.SIX[8] = data.nodes[23] + data.nodes[24] + data.nodes[25] + data.nodes[27] + data.nodes[28] + data.nodes[29];
//4*4

	data.SIX[9] = data.nodes[18] + data.nodes[19] + data.nodes[22] + data.nodes[30] + data.nodes[32] + data.nodes[33];
	data.SIX[10] = data.nodes[20] + data.nodes[21] + data.nodes[31] + data.nodes[35] + data.nodes[34] + data.nodes[26];
	data.SIX[11] = data.nodes[33] + data.nodes[22] + data.nodes[23] + data.nodes[27] + data.nodes[37] + data.nodes[36];
	data.SIX[12] = data.nodes[25] + data.nodes[26] + data.nodes[34] + data.nodes[39] + data.nodes[38] + data.nodes[29];
	data.SIX[13] = data.nodes[37] + data.nodes[27] + data.nodes[28] + data.nodes[42] + data.nodes[41] + data.nodes[40];
	data.SIX[14] = data.nodes[28] + data.nodes[29] + data.nodes[38] + data.nodes[44] + data.nodes[43] + data.nodes[42];
	data.SIX[15] = data.nodes[41] + data.nodes[42] + data.nodes[43] + data.nodes[47] + data.nodes[46] + data.nodes[45];
//5*5

	data.SIX[16] = data.nodes[48] + data.nodes[32] + data.nodes[33] + data.nodes[36] + data.nodes[51] + data.nodes[50];
	data.SIX[17] = data.nodes[34] + data.nodes[35] + data.nodes[49] + data.nodes[53] + data.nodes[52] + data.nodes[39];
	data.SIX[18] = data.nodes[51] + data.nodes[36] + data.nodes[37] + data.nodes[40] + data.nodes[55] + data.nodes[54];
	data.SIX[19] = data.nodes[38] + data.nodes[39] + data.nodes[52] + data.nodes[57] + data.nodes[56] + data.nodes[44];
	data.SIX[20] = data.nodes[55] + data.nodes[40] + data.nodes[41] + data.nodes[45] + data.nodes[59] + data.nodes[58];
	data.SIX[21] = data.nodes[43] + data.nodes[44] + data.nodes[56] + data.nodes[61] + data.nodes[60] + data.nodes[47];
	data.SIX[22] = data.nodes[59] + data.nodes[45] + data.nodes[46] + data.nodes[64] + data.nodes[63] + data.nodes[62];
	data.SIX[23] = data.nodes[46] + data.nodes[47] + data.nodes[60] + data.nodes[66] + data.nodes[65] + data.nodes[64];
	data.SIX[24] = data.nodes[63] + data.nodes[64] + data.nodes[65] + data.nodes[69] + data.nodes[68] + data.nodes[67];
//6*6

	data.SIX[25] = data.nodes[70] + data.nodes[50] + data.nodes[51] + data.nodes[54] + data.nodes[73] + data.nodes[72];
	data.SIX[26] = data.nodes[52] + data.nodes[53] + data.nodes[71] + data.nodes[75] + data.nodes[74] + data.nodes[57];
	data.SIX[27] = data.nodes[73] + data.nodes[54] + data.nodes[55] + data.nodes[58] + data.nodes[77] + data.nodes[76];
	data.SIX[28] = data.nodes[56] + data.nodes[57] + data.nodes[74] + data.nodes[79] + data.nodes[78] + data.nodes[61];
	data.SIX[29] = data.nodes[77] + data.nodes[58] + data.nodes[59] + data.nodes[62] + data.nodes[81] + data.nodes[80];
	data.SIX[30] = data.nodes[60] + data.nodes[61] + data.nodes[78] + data.nodes[83] + data.nodes[82] + data.nodes[66];
	data.SIX[31] = data.nodes[81] + data.nodes[62] + data.nodes[63] + data.nodes[67] + data.nodes[85] + data.nodes[84];
	data.SIX[32] = data.nodes[65] + data.nodes[66] + data.nodes[82] + data.nodes[87] + data.nodes[86] + data.nodes[69];
	data.SIX[33] = data.nodes[85] + data.nodes[67] + data.nodes[68] + data.nodes[90] + data.nodes[89] + data.nodes[88];
	data.SIX[34] = data.nodes[68] + data.nodes[69] + data.nodes[86] + data.nodes[92] + data.nodes[91] + data.nodes[90];
	data.SIX[35] = data.nodes[89] + data.nodes[90] + data.nodes[91] + data.nodes[93] + data.nodes[94] + data.nodes[95];*/

//求平均值
	data.average = (data.SIXANGLE[0]+data.SIXANGLE[1]+data.SIXANGLE[2]+data.SIXANGLE[3]																//2by2
					/*+data.SIXANGLE[4]+data.SIXANGLE[5]+data.SIXANGLE[6]+data.SIXANGLE[7]+data.SIXANGLE[8]												//3by3
					+data.SIXANGLE[9]+data.SIXANGLE[10]+data.SIXANGLE[11]+data.SIXANGLE[12]+data.SIXANGLE[13]+data.SIXANGLE[14]+data.SIXANGLE[15]					//4by4
					/*+data.SIX[16]+data.SIX[17]+data.SIX[18]+data.SIX[19]+data.SIX[20]+data.SIX[21]+data.SIX[22]+data.SIX[23]+data.SIX[24]	//5by5
	                +data.SIX[25]+data.SIX[26]+data.SIX[27]+data.SIX[28]+data.SIX[29]+data.SIX[30]+data.SIX[31]+data.SIX[32]+data.SIX[33]+data.SIX[34]+data.SIX[35] 	//6by6
	                */)/SIXANGLENUM;

//求方差：与期望之间的差距
	data.dispersion =
			(
//2by2
			pow((double)data.SIXANGLE[0]-data.average,2)+pow((double)data.SIXANGLE[1]-data.average,2)
			+pow((double)data.SIXANGLE[2]-data.average,2)+pow((double)data.SIXANGLE[3]-data.average,2))/SIXANGLENUM;
/*
//3by3
			+pow((double)data.SIX[4]-data.average,2)+pow((double)data.SIX[5]-data.average,2)
			+pow((double)data.SIX[6]-data.average,2)+pow((double)data.SIX[7]-data.average,2)
			+pow((double)data.SIX[8]-data.average,2)

//4by4
			+pow((double)data.SIX[9]-data.average,2)+pow((double)data.SIX[10]-data.average,2)
			+pow((double)data.SIX[11]-data.average,2)+pow((double)data.SIX[12]-data.average,2)
			+pow((double)data.SIX[13]-data.average,2)+pow((double)data.SIX[14]-data.average,2)
			+pow((double)data.SIX[15]-data.average,2)

//5by5
			+pow((double)data.SIX[16]-data.average,2)+pow((double)data.SIX[17]-data.average,2)
			+pow((double)data.SIX[18]-data.average,2)+pow((double)data.SIX[19]-data.average,2)
			+pow((double)data.SIX[20]-data.average,2)+pow((double)data.SIX[21]-data.average,2)
			+pow((double)data.SIX[22]-data.average,2)+pow((double)data.SIX[23]-data.average,2)
			+pow((double)data.SIX[24]-data.average,2)
//6by6

			+pow((double)data.SIX[25]-data.average,2)+pow((double)data.SIX[26]-data.average,2)
			+pow((double)data.SIX[27]-data.average,2)+pow((double)data.SIX[28]-data.average,2)
			+pow((double)data.SIX[39]-data.average,2)+pow((double)data.SIX[30]-data.average,2)
			+pow((double)data.SIX[31]-data.average,2)+pow((double)data.SIX[32]-data.average,2)
			+pow((double)data.SIX[33]-data.average,2)+pow((double)data.SIX[34]-data.average,2)
			+pow((double)data.SIX[35]-data.average,2)
			)/SIXANGLENUM;*/

//方差的平方：标准差
	data.deviation = sqrt(data.dispersion);

//初选
	data.primaryFit = data.average - data.deviation*sqrt((double)NODENUM);

	return data;
}


//*************fitness条件**********************//
void Fitness(void)
{
	int i;
	BestFitness = -100;
	WorstFitness = 100;
	sumOfPrimaryFit = 0;	//适应度

	for(i = 0; i < PARENTNUM; i++)
	{
		sumOfPrimaryFit += parents[i].primaryFit;

		if(BestFitness < parents[i].primaryFit)
		{
			BestFitness = parents[i].primaryFit;
			Best = i;
		}
		if(WorstFitness > parents[i].primaryFit)
		{
			WorstFitness = parents[i].primaryFit;
			Worst = i;
		}
	}

	sumOfFit = 0;

	for(i = 0; i < PARENTNUM; i++)
	{
		parents[i].fitness = (int)((SELECTION-1)*(parents[i].primaryFit - WorstFitness) 
									+ (BestFitness - WorstFitness));
		sumOfFit += parents[i].fitness;  //适度评分
	}
}

//*******************rullet wheel*****************//
int Selection(void)
{
	int i, s, point;
	if(sumOfFit == 0)
		sumOfFit = 1;
	point = rand()%sumOfFit;

	s = 0;
	for(i = 0; i < PARENTNUM; i++)
	{
		s += parents[i].fitness;
		if(point << s)
			return i;
	}
	return PARENTNUM-1;
}

//**************PMXcrossover******************//
turtle pmxCrossOver(int parentOne, int parentTwo)
{
	int i, j;
	int firstCutPoint, secondCutPoint;

	firstCutPoint = rand()%(NODENUM);
	secondCutPoint = rand()%(NODENUM - firstCutPoint)+firstCutPoint;

	for(i = firstCutPoint; i < secondCutPoint; i++)
		valuesOfChildren.nodes[i] = parents[parentOne].nodes[i];

	for(i = secondCutPoint; i < NODENUM; i++)
	{
		valuesOfChildren.nodes[i] = parents[parentTwo].nodes[i];
		for(j = firstCutPoint; j < secondCutPoint; j++)
		{
			if(valuesOfChildren.nodes[j] == valuesOfChildren.nodes[i])
			{
				while(valuesOfChildren.nodes[j] == valuesOfChildren.nodes[i])
				{
					j = firstCutPoint-1;
					valuesOfChildren.nodes[i] = parents[parentTwo].nodes[i];
				}
			}
		}
	}

	for(i = 0; i < firstCutPoint; i++)
	{
		valuesOfChildren.nodes[i] = parents[parentTwo].nodes[i];
		for(j = firstCutPoint; j < NODENUM; j++)
		{
			if(valuesOfChildren.nodes[j] == valuesOfChildren.nodes[i])
			{
				while(valuesOfChildren.nodes[j] == valuesOfChildren.nodes[i])
				{
					j = firstCutPoint - 1;
					valuesOfChildren.nodes[i] = parents[parentTwo].nodes[j];
				}
			}
		}
	}
	return valuesOfChildren;
}


//*********************mutation*******************//
turtle Mutation(turtle valuesOfChildren)
{
	int i, j;
	int temp;

	for(i = 0; i < NODENUM; i++)
	{
		if(rand()%100 < MUTATIONRATE)
		{
			j = rand()%NODENUM;
			temp = valuesOfChildren.nodes[i];
			valuesOfChildren.nodes[i] = valuesOfChildren.nodes[j];
			valuesOfChildren.nodes[j] = temp;
		}
	}
	return valuesOfChildren;
}


//*****************replacement**********************//
void Replacement(void)
{
	int i;

	for(i = 0; i < CHILDRENNUM; i++)
	{
		if(parents[children[i].parent2].primaryFit < children[i].primaryFit)
			parents[children[i].parent2] = children[i];
		else if(parents[children[i].parent1].primaryFit < children[i].primaryFit)
			parents[children[i].parent1] = children[i];
		else  parents[Worst] = children[i];
	}
}

void Show(turtle valuesOfChildren)
{
	int i;
	printf("count : %d ||    ", count);
	for(i = 0; i < NODENUM; i++)
		printf("\t%d", MakeSixAngle(valuesOfChildren).nodes[i]);
	for(i = 0; i < SIXANGLENUM; i++)
		printf("\t%d", MakeSixAngle(valuesOfChildren).SIXANGLE[i]);
	printf("\n");
}

void ResultShow(turtle valuesOfChildren)
{
	int i;
	printf("the time is %d //", count);
	for(i = 0; i <NODENUM; i++)
	{
		printf("\t%d",MakeSixAngle(valuesOfChildren).nodes[i]);
	}
	printf("\n");
	printf("Sum :");
	for(i = 0; i < SIXANGLENUM; i++)
	{
		printf("\t%d", MakeSixAngle(valuesOfChildren).SIXANGLE[i]);
	}
	printf("\n");
}