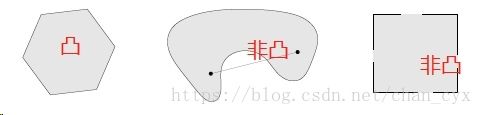
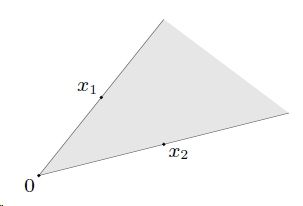
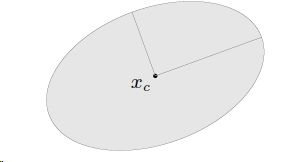
凸优化一（基本概念介绍）

背景知识

优化问题

• 凸优化是一类数学优化问题，介绍凸优化前先简单介绍数学优化问题。
• 优化问题定义（形式）：
  
  minimizef0 m i n i m i z e f 0
  
  
  subject tofi≤bi,i=1,...,m s u b j e c t   t o f i ≤ b i , i = 1 , . . . , m
  
  其中 x=(x1,…,xn) x = ( x 1 , … , x n ) （向量）是需要优化的变量
  f0:Rn→R f 0 : R n → R 是目标函数
  fi:Rn→R, i=1,⋯,m f i : R n → R ,   i = 1 , ⋯ , m 是m个约束函数
  最终要求解的值 x∗ x ∗ 是满足所有约束的条件下的所有向量中，使得目标函数取得最小值的向量

优化问题的具体应用场景

1. 投资组合优化
   
   • 优化变量：投资于不同投资方案的金额
   • 约束：预算/每个投资方案的最大或最小投资额/最小回报率
   • 目标函数：整个投资组合的风险回报率
2. 电子电路中的设备大小
   
   • 优化变量：设备的长和宽
   • 约束：制造工艺的限制/时间要求/最大面积
   • 目标函数：功耗
3. 数据拟合（机器学习中的一些算法，譬如svm等应用）
   
   • 优化变量：模型的参数
   • 约束：参数的限制/优先的条件
   • 目标函数：预测的误差函数（loss function等）

除了这些之外优化问题在其他各个领域还有很多的应用，总之优化问题在实际应用场景中是非常常见的。

如何解决优化问题

1. 一般的优化问题：都比较难解决，解决方法一般都是一种折中方案（逼近），由于非常长的计算时间，或者一直没有找到问题的解。

2. 一些特例（能够高效和可靠的被解决的一类问题）：

   • 最小二乘法问题
   • 线性规划问题
   • 凸优化问题

   下面的特例介绍

最小二乘

1. 问题定义（形式）
   
   minimize||Ax−b||22 m i n i m i z e | | A x − b | | 2 2
2. 最小二乘问题特性：
   
   • 存在可解析解： x∗=(ATA)−1ATb x ∗ = ( A T A ) − 1 A T b
   • 已有可靠和高效的算法解决此类问题
   • 计算时间复杂度： O(n2k), A∈Rk×n O ( n 2 k ) ,   A ∈ R k × n
   • 已经是一种成熟的工业技术(解决此类问题)
   • 最小二乘问题很容易识别

线性规划

1. 问题定义（形式）
   
   minimizecTx m i n i m i z e c T x
   
   
   subject toaTix≤bi,i=1,…,m s u b j e c t   t o a i T x ≤ b i , i = 1 , … , m
2. 特性：
   
   • 没有解析解
   • 已有可靠和高校的算法解决此类问题
   • 当 m≥n m ≥ n 时,计算时间复杂度 O(nm) O ( n m )
   • 已经是一种成熟的工业技术(解决此类问题)
   • 相对最小二乘来说比较难识别出来
   • 有一些技巧是把问题转化成线性规划问题求解

凸优化问题

1.问题定义（形式）

minimizef0(x) m i n i m i z e f 0 ( x )

subject tofi(x)≤bi,i=1,…,m s u b j e c t   t o f i ( x ) ≤ b i , i = 1 , … , m

目标函数和约束函数都是凸函数，即
fi(αx+βy)≤αfi(x)+βfi(y) f i ( α x + β y ) ≤ α f i ( x ) + β f i ( y ) ,其中
α+β=1,α≥0,β≥0 α + β = 1 , α ≥ 0 , β ≥ 0
2. 特性：

• 没有解析解
• 有可靠和高效的算法解决此类问题
• 计算时间复杂度 maxn3,n2m,F m a x n 3 , n 2 m , F ,其中F是约束函数 fi f i 的运算时间消耗以及他们各自的一次二次微分的总和
• 不像之前两种问题一样是一种成熟的工业技术，但是算是以及很成熟了（almost）
• 通常很难识别出来

• 有很多技巧把问题转换成凸优化问题形式求解

  最小二乘问题和线性规划问题是优化问题的特例

注：很多非凸问题也可以通过某种形式转化成凸优化问题来求解其近似解（一般在找不到原问题的解或求解原问题所需的时间复杂度太大的情形下使用）。这是解决一类问题的一种技巧，在深度学习的一些模型中经常用到。这是一种逼近的思想。

非线性优化

1. 局部优化方法（非线性规划）
2. 全局优化方法

凸优化中的一些定义

仿射集（Affine set）

定义：

仿射集是包含过两个不同的点的直线的所有点。
即 x=θx1+(1−θ)x2(θ∈R) x = θ x 1 + ( 1 − θ ) x 2 ( θ ∈ R )
如下图：



• 一个例子：线性方程组的解集{ x|Ax=b x | A x = b }
  
  • 推导：设 x1,x2 x 1 , x 2 是解集中两个不同的点，则有 Ax1=b,Ax2=b A x 1 = b , A x 2 = b ,且 A(θx1+(1−θ)x2)=θAx1+(1−θ)Ax2=θb+(1−θ)b=b A ( θ x 1 + ( 1 − θ ) x 2 ) = θ A x 1 + ( 1 − θ ) A x 2 = θ b + ( 1 − θ ) b = b ,又 Ax=b A x = b ,所以 x=θx1+(1−θ)x2 x = θ x 1 + ( 1 − θ ) x 2 ,得证。

注:所有的仿射集都可以用线性方程组的解集表示

凸集

定义

凸集是包含两个不同点之间的直线的所有点。
即 x=θx1+(1−θ)x2θ∈ x = θ x 1 + ( 1 − θ ) x 2 θ ∈ （0,1）

• 凸集C中， x1,x2∈C,0≤θ≤0⟹θx1+(1−θ)x2∈C x 1 , x 2 ∈ C , 0 ≤ θ ≤ 0 ⟹ θ x 1 + ( 1 − θ ) x 2 ∈ C
• 例子如下图：
  
  

凸组合和凸包

凸组合（convex combination）

定义： x1,x2,...,xk x 1 , x 2 , . . . , x k 的凸组合是满足 x=θ1x1+θ2x2+...+θkxk x = θ 1 x 1 + θ 2 x 2 + . . . + θ k x k ,其中 θ1+θ2+...+θk=1,θi≥0 θ 1 + θ 2 + . . . + θ k = 1 , θ i ≥ 0 的任意点x。

凸包（convex hull）

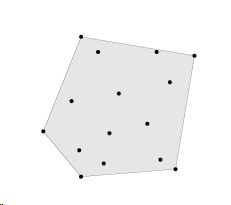
定义：conv S:集合S中的所有点的凸组合所成的集合。
如下图所示，黑点表示原始集合S,阴影部分表示conv S(凸包集合)



凸锥（Convex cone）

锥组合（conic (nonnegative) combination）

定义： x1,x2 x 1 , x 2 的锥组合是满足 x=θ1x1+θ2x2 x = θ 1 x 1 + θ 2 x 2 ,其中 θ2≥0,θ1≥0 θ 2 ≥ 0 , θ 1 ≥ 0 的任意点x。
如下图，阴影部分为锥组合所成的集合



凸锥

定义：convex cone:集合S中的所有点的锥组合所成的集合。

超平面和半空间

超平面（hyperplane）

定义：满足{ x|aTx=b x | a T x = b }  (a≠0)   ( a ≠ 0 ) 的集合。
如下图，其中b可以看作是截距或者是位移项，a是法向量。


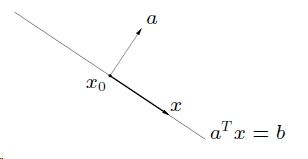
注：更多关于超平面的介绍请看之后关于SVM介绍一文中的预备知识

半空间（halfspaces）

定义：满足{ x|aTx≤b (a≠0) x | a T x ≤ b   ( a ≠ 0 ) }的集合。
如下图所示，阴影部分为半空间：


注：超平面是仿射集，同时是凸集，半空间是凸集但不是仿射集

• 从图中就可以很直观的看出来，下面以半空间为例子，来进行推导，其他情形推导方式一致。
• 推导：令 x1,x2 x 1 , x 2 为半空间中的点，则 aTx1≤b,aTx2≤b,x=θx1+(1−θ)x2, θ∈[0,1] a T x 1 ≤ b , a T x 2 ≤ b , x = θ x 1 + ( 1 − θ ) x 2 ,   θ ∈ [ 0 , 1 ] ,所以 aTx=aTθx1+aT(1−θ)x2≤θb+(1−θ)b=b a T x = a T θ x 1 + a T ( 1 − θ ) x 2 ≤ θ b + ( 1 − θ ) b = b ,得证。

球和椭圆

球(Euclidean ball)

定义： B(xc,r)= B ( x c , r ) = { x| ||x−xc||2≤r x |   | | x − x c | | 2 ≤ r }={ xc+ru| ||u||2≤1 x c + r u |   | | u | | 2 ≤ 1 },其中 xc x c 是圆心，r是半径。

椭圆

定义：{ x| (x−xc)TP−1(x−xc)≤1 x |   ( x − x c ) T P − 1 ( x − x c ) ≤ 1 }={ xc+Au| ||u||2≤1 x c + A u |   | | u | | 2 ≤ 1 },其中

P∈Sn++ P ∈ S + + n ,即P是对称正定矩阵,A是方阵，非奇异矩阵。



范数球和范数锥

范数

定义：满足以下条件的函数||.||

• ||x||≥0;  | | x | | ≥ 0 ;   当且仅当 x=0 x = 0 时， ||x||=0 | | x | | = 0
• 对 t∈R,  t ∈ R ,   ||tx||=|t| ||x|| | | t x | | = | t |   | | x | |
• ||x+y||≤||x||+||y|| | | x + y | | ≤ | | x | | + | | y | | （三角不等式）
  符号：||.||是一般范数， ||.||symb | | . | | s y m b 是特殊范数。

注：

• 范数（包括 Lp L p ）是将向量映射到非负值的函数，直观上，向量x的范数衡量从原点到点x的距离。
• Lp L p 范数定义: ||x||p=(∑i|xi|p)1p | | x | | p = ( ∑ i | x i | p ) 1 p
• L2 L 2 范数称为欧几里得范数，表示原点到向量x的欧几里得距离
• L∞ L ∞ 范数为最大范数，即 ||x||∞=maxi|xi| | | x | | ∞ = m a x i | x i |
• Frobenius范数，即 ||A||F=∑i,jA2i.j−−−−−−−√=tr（ATA）−−−−−−−√ | | A | | F = ∑ i , j A i . j 2 = t r （ A T A ） ,用于衡量矩阵大小。
• 两个向量的点积可以用范数来表示: xTy=||x|| ||y||cosθ x T y = | | x | |   | | y | | c o s θ
• 平方 L2 L 2 范数也常用来衡量向量的大小，可通过 xTx x T x 来计算

范数球

定义：{ x| ||x−xc||≤r x |   | | x − x c | | ≤ r },其中 xc x c 是圆心，r是半径。

范数锥

定义：{ (x,t)| ||x||≤t ( x , t ) |   | | x | | ≤ t }



注：欧几里得范数锥又叫第二顺序锥( L2 L 2 锥)，范数球和范数锥都是凸集

多面体(Polyhedra)

定义： Ax≤b,Cx=d A x ≤ b , C x = d ,
其中 A∈Rm×n, C∈Rp×n A ∈ R m × n ,   C ∈ R p × n ,不等式 ≤ ≤ 是分量式不等式，即每个维度上这个不等式都成立。


注：多面体是有限个超平面和半空间的交集，如上图所示

半正定锥

符号定义：

• Sn S n 是 n×n n × n 的对称矩阵集
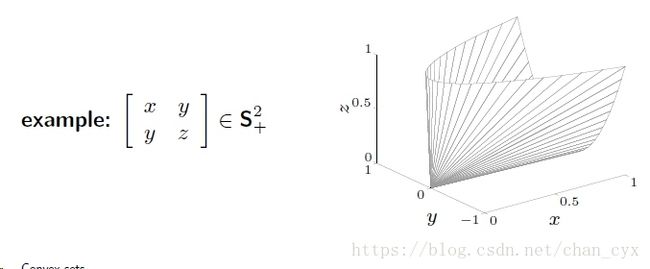
• Sn+= S + n = { X∈Sn|X≥0 X ∈ S n | X ≥ 0 }是 n×n n × n 半正定矩阵集,其中 X∈Sn+⟺ X ∈ S + n ⟺ (对所有的z) zTXz≥0 z T X z ≥ 0 , $S_+^n是凸锥（convex cone）
• Sn++= S + + n = { X∈Sn|X=0 X ∈ S n | X = 0 }是 n×n n × n 正定矩阵
  
  

参考

• 《Convex Optimization》 – Stephen Boyd and Lieven Vandenberghe