Matlab 学习笔记 (部分内容系转载)
由于要参加数学建模比赛的原因,我需要在不到一周的时间内初步地学习Matlab。
因此,我希望把我在学习过程中阅读的资料记录下来,方便跟我一样需要在较短时间内速成Matlab的同学。
基本上我记录的东西都是从网上的资料总结而来。所以这篇文章更偏向是一个资料汇总类的东西。
凡是给过我帮助的资料我都已经列在“参考资料”里,为了美观就不在具体内容里标注引用了,请见谅。
另外,还有部分内容引自《MATLAB在数学建模中的应用》,一并感谢。
我使用的MATLAB版本是r2012a。绝大部分代码我都在本机运行过。由于资源的来源很多,代码风格可能不太一致。
博主最终学了一点点就干别的去了。。数模比赛也悲剧了。。所以此文烂尾了。。不过博主如果以后还要学习matlab,可能会再来更新也说不定。
一、基本操作
M语言文件的后缀名是.m。Matlab特有的数据存储格式是.mat。
Matlab默认的编程界面是控制行窗口,要新建.m文件可以点击File->New->Script。
常规操作我就不过多解释了。
若要了解某一函数的调用方式,直接在命令行窗口输入“help XXX”即可。
给出一些参考资料:
《Matlab操作方法》
《MATLAB数据类型》
《 matlab中数组元素引用》二、数据交互
1、从纯数据txt文件中读取数据
使用简单粗暴的LOAD/SAVE函数。
LOAD可以读MAT-file data或者用空格间隔的格式相似的ASCII data。SAVE可以将MATLAB变量写入MAT-file格式或者空格间隔的ASCII data。
eg:
M = load('test.txt') % 从input.txt中读一个矩阵M。
M = M + 5 % 把M的每个元素加上5
save output M % 把M保存在output.mat文件中
save output.txt M -ascii % 把M以ASCII形式保存在output.txt文件中2、从txt文件中按照特定格式读取数据
使用TEXTREAD/STRREAD函数
[A,B,C,…] = textread(filename,format,N)
其中括号里面变量的个数必须和format中定义的个数相同。 如果每N行相同格式的数据,可采用[A,B,C,…] = textread(filename,format,N)的语法,读取N次。
textread不用先fopen那个文件,适用于格式统一的txt文件的一次性大批量读取。textread读取某个文件后,下次再用textread读取这个文件时,还是会从文件头开始读取。
eg:
[data1,data2,data3,data4,data5] = textread('output.txt','%f %f %f %f %s',150,'delimiter',','); % 以','为分隔符
[data1,data2,data3,data4] = textread('output.txt','%n %n %n %n','delimiter', ',','headerlines', 5); % 跳过开头的5行
[data1,data2,data3,data4] = textread('output.txt' , '%s %s %*f %d %s', 1) % ‘*f ’告诉textread跳过一个浮点数。
[data] = textread('output.txt','%s %*[^\n]'); % [^\n] 就是一直读到行尾,%*[^\n] 是一直跳到行尾。可用于只读取第一列
[data1,data2,data3,data4] = textread('output.txt','%s test %d %f %d %s', 1) % 忽略‘test’,只读取后面的数字3、从txt文件中读取特定区域的数据:
下面这个函数是取filein中的第line行写入fileout中的程序:
function dataout=dataread(filein,fileout,line)
fidin=fopen(filein,'r');
fidout=fopen(fileout,'w');
nline=0;
while ~feof(fidin) % 判断是否为文件末尾
tline=fgetl(fidin); % 从文件读行
nline=nline+1;
if nline==line
fprintf(fidout,'%s\n',tline);
dataout=tline;
end
end
fclose(fidin);
fclose(fidout); 调用格式:dataout=dataread(filein,fileout,line)
如果txt文件数据是矩阵形式的,而没有其它的文字,用下面的程序就可以读任意行任意列的数据
a=textread('ll.txt');
t=a(1:43,4:10); % 1:43是1到43行,4:10是4到10列的数据4、读取Excel文件
使用xlsread、xlswrite函数
[data] = xlsread('filename') % 从excel文件filename的第一个工作页中读取所有的数据到double型数据data中。它忽略头行、头列、尾行、和尾列的所有单元为文本的行列,其他单元中的文本全部读取为NaN。
[data] = xlsread('filename', -1) % 手动框选要读取的数据块
[data] = xlsread('filename', sheet, 'range') % filename, sheet, range 文件名、sheet名、范围(eg:'A1:D2'就指定了一个子矩阵的对角线范围)
[data] = xlswrite('filename', 'M', sheet, 'range') % filename, M, sheet, range 文件名、数据、sheet名、范围如果要读取批量的文件
首先将多个文件进行批量重命名例如file1.xls,file2.xls,file3.xls,...
然后用循环的方式实现:for i=1 : 100
filename=['file', num2str(i), '.xls'];
num=xlsread(filename)
end5、小tips
1) 文本文件中的每个字节的最高位都是0,也就是说文本文件使用了一个字节中的七位来表示所有的信息,而二进制文件则是将字节中的所有位都用上了。在用文本文件方式打开文件时,会将字符自动转换成ASCII码。
2)当excel中有合并单元格时,任何一个合并前的单元格的名字都会指代整个合并后的单元格,而将整个单元格读入。
6、参考资料
《MATLAB操作txt总结》
《matlab中如何读取TXT数据文件》
《matlab中读取txt数据文件》
《关于matlab中textread》
《matlab与excel xlsread、xlswrite实用方法》
《MATLAB读写Excel》
三、数据拟合
1、plot函数的使用
1. plot函数的输入参数是矩阵形式
(1) 当x是向量,y是有一维与x同维的矩阵时,则绘制出多根不同颜色的曲线。曲线条数等于y矩阵的另一维数,x被作为这些曲线共同的横坐标。
(2) 当x,y是同维矩阵时,则以x,y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
(3) 对只包含一个输入参数的plot函数,当输入参数是实矩阵时,则按列绘制每列元素值相对其下标的曲线,曲线条数等于输入参数矩阵的列数。
当输入参数是复数矩阵时,则按列分别以元素实部和虚部为横、纵坐标绘制多条曲线。
2. 含多个输入参数的plot函数
调用格式为:
plot(x1,y1,x2,y2,…,xn,yn)
(1) 当输入参数都为向量时,x1和y1,x2和y2,…,xn和yn分别组成一组向量对,每一组向量对的长度可以不同。每一向量对可以绘制出一条曲线,这样可以在同一坐标内绘制出多条曲线。
(2) 当输入参数有矩阵形式时,配对的x,y按对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
3. 具有两个纵坐标标度的图形
在MATLAB中,如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy绘图函数。调用格式为:
plotyy(x1,y1,x2,y2)
其中x1,y1对应一条曲线,x2,y2对应另一条曲线。横坐标的标度相同,纵坐标有两个,左纵坐标用于x1,y1数据对,右纵坐标用于x2,y2数据对。
4. 图形保持
hold on/off命令控制是保持原有图形还是刷新原有图形,不带参数的hold命令在两种状态之间进行切换。
5. 设置曲线样式
MATLAB提供了一些绘图选项,用于确定所绘曲线的线型、颜色和数据点标记符号,它们可以组合使用。例如,“b-.”表示蓝色点划线,“y:d”表示黄色虚线并用菱形符标记数据点。当选项省略时,MATLAB规定,线型一律用实线,颜色将根据曲线的先后顺序依次。
要设置曲线样式可以在plot函数中加绘图选项,其调用格式为:
plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)
2、使用polyfit()一元多项式拟合
polyfit(X, Y, N):多项式拟合函数,返回降幂排列的多项式系数。X是因变量,Y是自变量,N是拟合函数的最高幂次。
polyval(p, Xi):计算多项式的值
在EXCEL文件中存储如下数据:
新建.m文件输入以下代码:
x = xlsread('in.xlsx', 1, 'B1:J1');
y = xlsread('in.xlsx', 1, 'B2:J2');
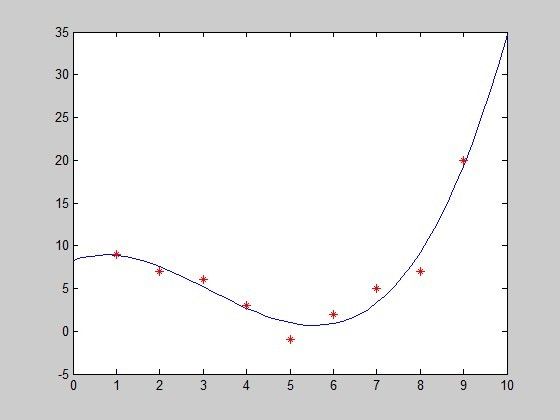
P = polyfit(x, y, 3); % 用三次方函数拟合y相对于x的系数。返回降幂排列的多项式系数
xi = 0: .2: 10; % 0~10,以0.2为步进的序列
yi = polyval(P, xi);
plot(xi, yi, x, y, 'r*'); % 绘制曲线和散点运行结果:
还有两种效果相同的写法:
x = xlsread('C:\Users\Administrator\Desktop\in.xlsx', 1, 'B1:J1');
y = xlsread('C:\Users\Administrator\Desktop\in.xlsx', 1, 'B2:J2');
P = polyfit(x, y, 3);
xi = linspace(min(x), max(x));
yi = polyval(P, xi);
plot(x, y, '*', xi, yi); x=[1; 1.5; 2; 2.5; 3];
y=[0.9; 1.7; 2.2; 2.6; 3];
P = fittype('poly3');
f = fit(x, y, P); % fit函数的参数只能是列变量
plot(f, x, y);当然使用图形化界面也是可以的。
先画出数据点: plot(xi, yi, x, y, 'r*');
然后在出现的图形界面中,选择Tools -> Basic Fitting
可以分别用多阶函数进行拟合。选项和效果如下图:
3、自定义函数一元曲线拟合
用fittype()定义拟合函数,然后用 fit() 函数拟合。
fittype函数原型如下:
fittype(libname)
fittype({expr1,...,exprn}, Name, Value,...)
fittype()中independent是自变量,coefficients是因变量。需注意 fit() 函数的因变量和自变量都要是列向量。
x = [1; 1.5; 2; 2.5; 3];
y = [0.9; 1.7; 2.2; 2.6; 3];
f = fittype('a * x .^ 2 + b * x + c', 'independent', 'x', 'coefficients', {'a', 'b', 'c'});
P = fit(x, y, f) % 用指定函数拟合y相对于x的系数。注意这里的数据必须是列向量
xi = 0: .2: 5; % 0~5,以0.2为步进的序列点
yi = P(xi);
plot(x, y, 'r*', xi, yi, 'b-'); % 绘制曲线和散点关于ploy()函数的更多调用方式以及其它图形的绘制方法,请直接移步《MATLAB曲线绘制》。
4、regress()函数多元函数拟合
regress(y,x) 的重点与难点是如何加工处理矩阵x。
y是函数值,一定是只有一列。
也即目标函数的形式是由矩阵X来确定
如s=a+b*x1+c*x2+d*x3+e*x1^2+f*x2*x3+g*x1^2,
一定有一个常数项,且必须放在最前面(即x的第一列为全1列)
X中的每一列对应于目标函数中的一项(目标函数有多少项则x中就有多少列)
X=[ones, x1, x2, x3, x1.^2, x2.*x3,x1.ˆ2] (剔除待定系数的形式)
用regress()函数对人口预测模型拟合:
Y = [33815 33981 34004 34165 34212 34327 34344 34458 34498 34476 34483 34488 34513 34497 34511 34520 34507 34509 34521 34513 34515 34517 34519 34519 34521 34521 34523 34525 34525 34527]
T = [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]
for t = 1:30
x(t) = exp(-t);
y(t) = 1/Y(t);
end
reshape(x, 30, 1);
reshape(y, 30, 1);
c = ones(30,1);
f = regress(y',[c,x']);
for j = 1:30,
Y(j) = 1/ (f(1) + f(2) * exp(-j));
end
plot(T, Y)5、nlinfit()多元任意函数拟合
顺序([b,r,j]=nlinfit(x,y,’…’, b0)y为列向量;x为矩阵,无需加全1列,x,y就是原始的数据点,(x/y正顺序,所以x不要加全1列)需预先编程(两个参数,系数向量,各变量的矩阵/每列为一个变量)
存在的问题:不同的beta0,则会产生不同的结果,如何给待定系数的初值以及如何分析结果的好坏,如出现警告信息,则换一个待定系数试一试。因为拟合本来就是近似的,可能有多个结果。
1. 重点(难点)是预先编程序(即确定目标函数的形式,而regress的目标函数由x矩阵来确定,其重难点为构造矩阵a)
2. x/y顺序—列向量----x/y是原始数据,不要做任何修改
3. 编程: 一定两个形参(beta,x)a=beta(1); b=beta(2);c=beta(3);… x1=x(:,1); x2=x(:,2); x3=x(:,3); 即每一列为一个自变量
4. regress/nlinfit都是列向量
5. regress:有n项(n个待定系数),x就有n列;nlinfit:有m个变量则x就有m列
6、最小二乘法拟合线性回归模型
以人口预测模型为例。
因为Logisic曲线的基本形式为
y = 1 / (a + b * eps(- t))
所以只要令y' = 1 / y,x' = eps(- t)。
就可以转化为直线模型 y' = a * x' + b。
然后用最小二乘法进行回归拟合即可。
Y=[33815 33981 34004 34165 34212 34327 34344 34458 34498 34476 34483 34488 34513 34497 34511 34520 34507 34509 34521 34513 34515 34517 34519 34519 34521 34521 34523 34525 34525 34527]
T=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]
for t = 1:30,
x(t)=exp(-t);
y(t)=1/Y(t);
end
c=ones(30,1);
X=[c,x'];
B=inv(X'*X)*X'*y'
for j=1:30,
Y(j)=1/(B(1,1)+B(2,1)*exp(-j));
end
plot(T,Y)详细代码如下:
% 删除工作空间中的项目,释放系统内存
clear
% 清除命令窗口
clc
% 读入人口数据(1971-2000年)
Y=[33815 33981 34004 34165 34212 34327 34344 34458 34498 34476 34483 34488 34513 34497 34511 34520 34507 34509 34521 34513 34515 34517 34519 34519 34521 34521 34523 34525 34525 34527]
% 读入时间变量数据(t=年份-1970)
T=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]
% 线性化处理
for t = 1:30
x(t)=exp(-t);
y(t)=1/Y(t);
end
% 计算,并输出回归系数B
c=zeros(30,1)+1;
X=[c,x'];
B=inv(X'*X)*X'*y'
for i=1:30,
% 计算回归拟合值
z(i)=B(1,1)+B(2,1)*x(i);
% 计算离差
s(i)=y(i)-sum(y)/30;
% 计算误差
w(i)=z(i)-y(i);
end
% 计算离差平方和S
S=s*s';
% 回归误差平方和Q
Q=w*w';
% 计算回归平方和U
U=S-Q;
% 计算,并输出F检验值
F=28*U/Q
% 计算非线性回归模型的拟合值
for j=1:30,
Y(j)=1/(B(1,1)+B(2,1)*exp(-j));
end
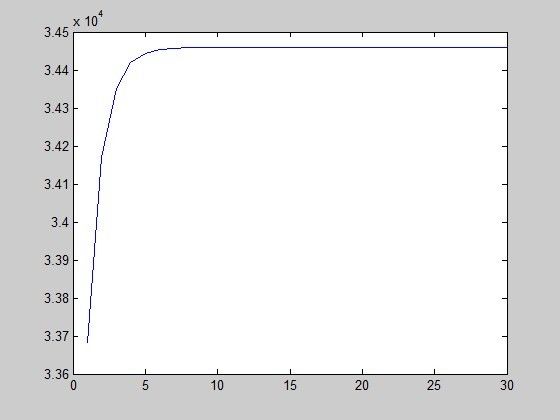
% 输出非线性回归模型的拟合曲线(Logisic曲线)
plot(T,Y)运行效果如下:
7、曲线拟合工具箱
在命令行窗口直接输入'cftool'打开。或者单击左下角的"Start"按钮,选择"Toolboxes"-->"Curve Fitting",打开"Curve Fitting Tool"。
这个工具箱的使用方式比较简单,详见《Matlab曲线拟合工具箱CFTOOL实例解析》。
8、小tips
1)MATLAB中的数组是按列存储的。并且为数组元素分配了唯一的index,对于矩阵a[n][m],a[i][j]的index = j * n + i。
2) 用regress函数做多元线性回归拟合的时候,要在X矩阵前加一个全1列,当做常数项。可以用到函数 ones(n, m) / zeros(n, m) 代表一个n * m 的全0 / 1 矩阵
3)fit()函数的X矩阵必须是列向量,可以用到一个函数B = reshape(A, n, m);
9、参考资料
《 Matlab 线性拟合 & 非线性拟合》《 Matlab曲线拟合工具箱CFTOOL实例解析》
《MATLAB曲线绘制》
《matlab多元非线性回归》
四、规划问题
1、线性规划
MATLAB中线性规划的标准形式是
min z = sigma(cj * xj)
即 sigma(aij * xj) <= bi
满足不等式的解成为可行解,使目标函数最小的解称为最优解。
MATLAB中解线性规划的标准调用形式是:
[X,FVAL,EXITFLAG,OUTPUT,LAMBDA] = linprog(f,A,b,Aeq,beq,LB,UB,X0)
f 是所求目标函数的系数矩阵。
A, b分别是x和常数项的系数矩阵。
Aeq和beq代表等式约束条件 Aeq * X = beq。
LB和UB代表x值的上下界,LB <= xi <= UB。
X0代表X的缺省值,该选项只适用于中型问题,默认大型问题时将忽略初值。
FVAL是目标函数最优解的值。
X是取得最优解时X的取值,FVAL = f' * X。
exitflag为终止迭代的错误条件:若exitflag>0表示函数收敛于解x, exitflag=0,表示超过函数估值或迭代的最大数字,exitflag<0表示函数不收敛于解x。
lambda为解x的Lagrange乘子。若lambda=lower表示下界LB,lambda=upper表示上界UB,lambda=ineqlin表示不等式约束,lambda=eqlin表示等式约束,lambda中的非0元素表示对应的约束是有效约束。
eg:
min z = 2 * x1 + 3 * x2 + x3
x1 + 4 * x2 + 2 * x3 >= 8
3 * x1 + 2 * x2 >= 6
x1, x2, x3 >= 0
代码如下:
f = [2; 3; 1];
A = [-1 -4 -2; -3 -2 0; -1 0 0; 0 -1 0; 0 0 -1];
b = [-8; -6; 0; 0; 0];
[x, fval] = linprog(f, A, b, [], [])
或者
f = [2; 3; 1];
A = [-1 -4 -2; -3 -2 0];
b = [-8; -6];
[x, fval] = linprog(f, A, b, [], [], zeros(3, 1))MATLAB中非线性规划的标准形式如下:
min f(x)
AX <= B
Aeq * X = Beq
C(X) <= 0
Ceq(X) = 0
标准型为:
min F(X)
AX<=b
Aeq * X <= beq
G(X) <= 0
Ceq(X) = 0
VLB <= X <= VUB
其中X为n维变元向量,G(X)与Ceq(X)均为非线性函数组成的向量,其它变量的含义与线性规划、二次规划中相同。
用Matlab求解上述问题,基本步骤分三步:
1. 首先建立M文件fun.m,定义目标函数F(x):
function f = fun(X);
f = F(X);
2若约束条件中有非线性约束:G(X) 或Ceq(X)=0,则建立M文件nonlcon.m定义函数G(X)与Ceq(X):
function [G,Ceq]=nonlcon(X)
G=...
Ceq=...
3. 调用函数fmincon()
[x,fval,exitflag,output] =fmincon(‘fun’,X0,A,b,Aeq,beq,VLB,VUB,’nonlcon’,options)
3、二次规划
若某非线性规划的目标函数为 x 的二次函数,约束函数又全是线性的,则称这种规划为二次规划
标准型为:
min z =1 / 2 * XTHX + fTX (H是实对称矩阵)
AX <= b
quadprog() 函数的调用方式如下:
[X, FVAL, EXITFLAG, OUTPUT, LAMBDA] = quadprog(H, f, A, b, Aeq, beq, LB, UB, X0, OPTIONS)
eg:
min z = -2 * x1 - 6 * x2 + x1 ^ 2 - 2 * x1 * x2 + 2 * x2 ^ 2
x1 + x2 ≤ 2
-x1 + 2 * x2 ≤ 2
x1 ≥ 0, x2 ≥ 0
H = [1 -1; -1 2];
c = [-2 ;-6];
A = [1 1; -1 2];
b = [2;2];
[x, z] = quadprog(H, c, A, b, [], [], [0;0])另外还可以利用罚分数法,可将非线性规划问题的求解转化为求解一系列无约束极值问题,因而也称这种方法为序列无约束最小化技术,简记为SUMT。
4、0-1分数规划
0-1分数规划采用的是隐枚举法。譬如,求f(X)最大值时,试探得出一个解使得f(X) = 5,那么就添加一个条件f(X) >= 5,继续试探。
5、随机取样计算法
rand(n, m)函数可以产生一个在(0, 1)之间均匀分布的随机数组成的 n * m 矩阵。
用rand('state',S)设定种子。S为35阶向量,最简单的设为0就好。可以考虑rand('state', 100 * sum(clock) * rand(1))。
6、参考资料
《MATLAB中的线性规划问题》
《非线性规划及matlab实现》
《matlab随机函数rand使用中应注意的问题》
《时间计时函数tic-toc等》