视觉里程计的入门实践
1.典型特征
1)前言
在SLAM系统问题中,根据经典的框架,分为:前端、后端、回环、建图四大部分。所谓前端,就是视觉里程计的部分,视觉里程计又称前端。是视觉构建中,前端的作用就是把图像的信息处理为相关后续可以使用的计算向量,就是通过图像得出相机的运动信息,为后续计算提供可能。
> 图像处理中,特征点指的是图像灰度值发生剧烈变化的点或者在图像边缘上曲率较大的点(即两个边缘的交点)。图像特征点在基于特征点的图像匹配算法中有着十分重要的作用。图像特征点能够反映图像本质特征,能够标识图像中目标物体。通过特征点的匹配能够完成图像的匹配。
在传统的计算机视觉中,特征点是描述图像特征的像素描述,一般由像素特征和像素描述组成,这里的像素描述也可以称为特征描述。在我们这一章所讲述的视觉里程计中,在像素级的描述,将视觉里程计的算法大致分为2大类,一类为我们的特征点法,一类为我们的直接法。
2)特征点
为了准确的估计出相机的运动信息,我们需要选择合适的特征点。图像的本质是像素,像素的本质是色彩和亮度,在像素的层面上考虑,所谓特征点就是具有代表性的像素点或者像素点的集合。当然,这个特征点必须足够稳定,足够有代表性,否则就不能描述出一个图像的特征。
图像中,角点、边缘、块等等,都可能出现比较有代表性的特征点,所谓代表性,就是它比较特殊。在传统的角点特征点上,研究出现了很多特征点提取的相关算法,比如:Harris、GFTT等等,各有千秋,那么在SLAM系统中,在像素特征点的层面上,比较有代表性的特征点有哪些呢?
特征点,在学术界的描述为:关键点+描述中组成。在SLAM中,比较合适、典型的特征点就是ORB特征点。
3)ORB
ORB是是ORiented Brief的简称。他的提出论文的原文在:Ethan Rublee and Vincent Rabaud and Kurt Konolige and Gary Bradski, ORB: an efficient alternative to SIFT or SURF, ICCV 2011
其由2部分组成:FAST角点和BRIEF描述子。
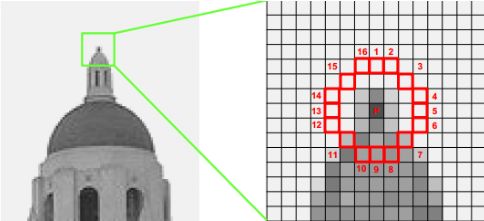
FAST角点,正如其名,特点就是快。为什么快呢,其实也非常简单,就是其只比较像素的亮度值,其具体的方法和理论这里不做赘述。
ORB特征点对其的改进有哪些呢?就是利用图像金字塔,建立了尺度不变性,何为图像金字塔,就是可以理解为多个大小图像的合集。除此之外还有什么呢?还有尺度不变性,这是如何构建的呢?其实也非常简单,利用灰度质心法,简单得出一个方向向量。就大大改进了FAST角点。
BRIEF的优点当然在于速度快,缺点当然也很多:不具备旋转不变性、对噪声敏感、不具备尺度不变性等等,看到这里,是不是感觉上面的改进有点聪明了。BRIEF描述子是用二进制进行描述的描述向量。对于关键点的描述子,BRIEF描述子也非常简单粗暴,直接在关键点附近随机生成像素,通过二进制编码组成描述向量。这里就对关键点进行了描述。
2.特征代码实践
1)特征匹配
特征匹配有多种方式方法:暴力(Brute-Force)匹配:一种描述符匹配算法,该方法会比较两个描述符,并产生匹配结果列表,第一个描述符的所有特征都拿来和第二个进行比较。除此之外,还有K-最近邻(knn)匹配:在所有的机器学习suan算法中,knn可能是最简单的。
让我们用代码实践一下特征匹配算法:
#include 2)ORB特征
对于ORB特征,我们也用代码实践一下加深理解:
//以下代码来自GITHUB
//参考视觉slam十四讲
//仅作参考
#include 4.总结
以上,我们就简单入门了视觉里程计中的ORB相关特征,特征是图像最基础的概念之一,在传统图像算法中,这是非常重要的知识点,ORB,这是一个近年来非常经典的特征描述,希望可以帮助到大家理解。