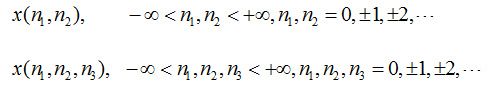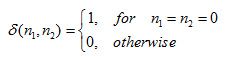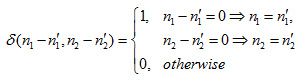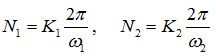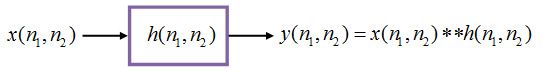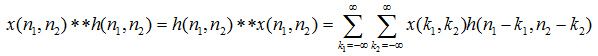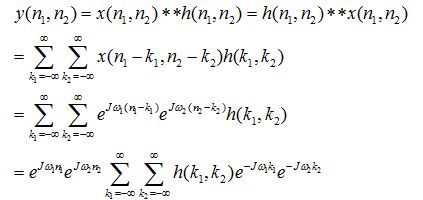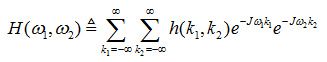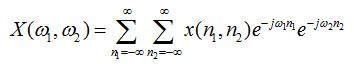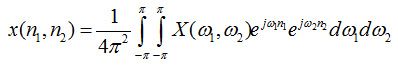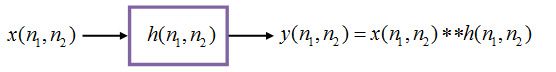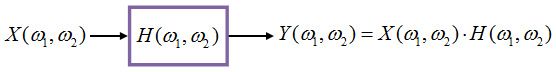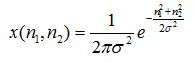如何构造频域滤波器——图像频域滤波的信号与系统基本理论

如何构造频域滤波器——图像频域滤波的信号与系统基本理论

上一篇博文“10句话读懂图像频域滤波——不能不知道的信号与系统基本理论”总结了图像频域滤波基本理论的要点，本文将对图像频域滤波的信号与系统基本理论做一简要梳理，作为上一篇博文的补充。包括基本信号维度与形式、复指数信号及其周期性、LSI系统、傅里叶变换、卷积定理、图像频域滤波，以及如何构造频域滤波器等内容。

摘要：采用了邻域加权累加求和的方式替换滤波核中心像素值的滤波器，都属于使用了卷积运算的滤波器，这类滤波器构成的系统为线性移不变(LSI)系统。卷积定理告诉我们：图像与滤波核在空域的卷积运算等价于图像频谱X(ω₁,ω₂)与滤波器频率响应H(ω₁,ω₂)的乘积运算。因此，滤波器的频率响应H(ω₁,ω₂)决定了输入图像频域X(ω₁,ω₂)哪中些频率分量可以通过甚至被放大，哪些频率分量会被衰减直至不能通过。简言之：图像在空域的卷积运算实现了频域的滤波。

1.连续信号与离散信号

（1）信号

包含某个感兴趣现象的某些行为或本质的函数可称为信号。在自然界中，对某些随时间或空间变化的量的观测值就是潜在的信号。例如，随时间变化的心电图可记为x(t)，强度x为随时间t变化的1维信号，而自变量t连续变化，所以x(t)为连续信号。

（2）二维与三维离散信号

为了方便计算机存储和处理，连续信号都需要转换成离散的数字信号。

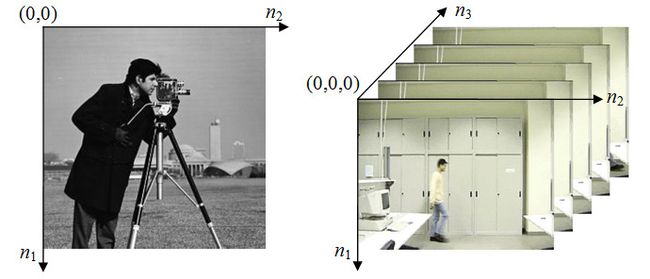
离散信号的典型代表就是数字图像：对于二维图像，它记录了光场在二维空间的强度分布信息；如果加上时间维度，则数字图像记录了光场在空间和时间上的三维强度分布信息。数字信号通常都通过采样与量化得到，如数字图像中的像素值及其坐标值都是离散量：对坐标值进行离散化称之为采样，对强度值进行离散化称为量化。

二维和三维离散信号可记为：

灰度图像是典型的二维离散信号，彩色图像（3通道）或视频信号则是典型的三维离散信号。

二维灰度图像信号                                                      三维视频图像信号

（3）离散单位冲激函数

单位冲激函数是信号与系统理论中最基本的分析工具，对于数字图像处理的理论分析，我们关注离散单位冲激函数。位于(0,0)点的离散单位冲激函数定义为：

改变冲激函数位置到(n₁',n₂')：

离散单位冲激函数可以理解为：仅在某一点处强度为1，其他位置均为0的信号。

（4）复指数信号

一个在频率ω₁和ω₂处的二维复指数信号记为

复指数信号可能是信号处理中最重要的信号之一，它如此重要的原因主要有两个：

• 复指数信号是LSI系统的特征方程（下面将解释什么是LSI系统），它通过LSI系统后频率不发生任何变化；

• 复指数信号可以成为任何其他信号的基本构成部分(“Building Blocks” of anysignal)，也就是说，可以将任意信号写成复指数信号的加权和的形式。

由欧拉方程可知二维复指数信号可展开为

以下是离散复指数信号的一些性质

• 离散复指数信号对频率ω₁和ω₂具有周期性

• 离散复指数信号对空间位置n₁和n₂有可能具有周期性，需要和满足一定条件：当ω能被2π整除时，离散复指数信号具有空间周期N₁和N₂（下式中K为正整数）。

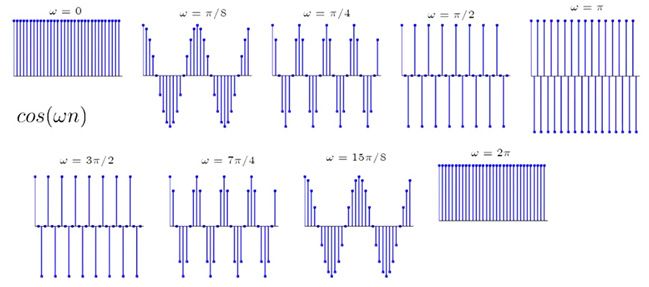
复指数信号可以是构成任意信号的基。为了说明复指数信号在空间上的周期性，我们挑选一组频率ω，使得复指数信号在空间上（即n₁和n₂）具有周期性。下面两幅图分别展示了选择特殊的频率ω时，一维cos(ωn)信号与二维cos(ω₁n₁+ω₂n₂)信号的空间周期性。

一维cos(ωn)信号的周期性

1D离散cos(ωn)信号的周期性

当ω=π/8时，N=2π/ω=2π/(π/8)=16，该信号空间周期为16个像素

当ω=π/4时，N=2π/ω=2π/(π/4)=8，该信号空间周期为8个像素

当ω=π时，N=2π/ω=2π/π=2，该信号空间周期为2个像素，此时为空间频率的最大值

当ω>π后，因cos(ω)= cos(2π-ω)，所以信号将重复上述空间周期性。如ω=3π/2时，信号形式与ω=π/2相同

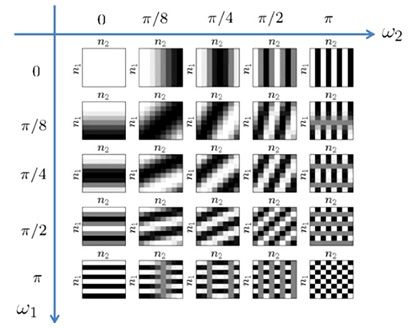
二维cos(ω₁n₁+ω₂n₂)信号的周期性

将上述对一维cosine信号的分析扩展到二维，可以得到在垂直于水平方向的两个频率ω₁和ω₂取所选的各值时的二维频率图像如下图所示，图中每个方格子为一个8×8像素矩阵。

2D离散cos(ω₁n₁+ω₂n₂)信号的周期性

当ω₁=0，ω₂=0时，垂直和水平方向都没有周期性，因此图像为全白，频率为(0,0)；

当ω₁=π，ω₂=0时，垂直方向空间周期为2个像素（见一维的分析），水平方向没有周期性，因此频谱图像为水平黑白相间的条纹，且条纹周期为2个像素。

当ω₁=π，ω₂=π时，垂直和水平方向空间周期均为2个像素，频谱图综合到一起就成了黑白相间的棋盘格子，无论水平方向还是垂直方向的空间周期均为2个像素。

由上图可见，离散复指数信号作为任意信号的基本组成单元可以包含图像中不同的频率成分。

2.LSI系统

任意维度的信号处理中，最重要的运算之一就是LSI系统中的卷积运算。LSI系统可由其冲激响应唯一描述。

对数字图像处理的最简单的描述就是输入一幅图像x(n₁,n₂)，为达到某些目标（如图像滤波等），将某些变换应用到输入图像从而得到输出图像y(n₁,n₂)。从信号与系统的角度来看，这一变换过程可看做一个LSI系统对输入信号的响应过程。

（1）2维系统

假设有一个2维系统T，输入图像x(n₁,n₂)，输出图像y(n₁,n₂)，如下图所示

例如，一个将灰度值取反的变换就是一个2维系统：

系统的众多属性中我们关注线性(Linearity)与空间不变性(Spatial Invariance)，因为这两个性质与图像滤波系统密切相关，本文讨论的频域滤波采用了邻域加权累加值来替换像素值的滤波器可以视为LSI系统，因为它满足线性与空间移不变性。

（2）线性系统-Linear System

如果一个2维系统为线性系统，则该系统满足：

线性系统有如下性质：

• 当α₂=0时，T[α₁x₁(n₁,n₂)]= α₁T[x₁(n₁,n₂)]，即常系数可以拿到系统外

• 当α₁=-α₂，x₁(n₁,n₂)= x₂(n₁,n₂)时，T[0]=0

（3）移不变系统-Spatially Invariant System (SI)

移不变系统指的是：系统与坐标原点的位置无关(the system does not care about the location of the axis)。

移不变系统的定义为：如果一个系统y(n₁,n₂)= T[x(n₁,n₂)]为空间移不变系统，则该系统满足

线性与移不变性相互独立。非线性系统可以是移不变系统；线性系统，也可能是非移不变系统。

（4）线性移不变系统-LSI System

如果一个系统同时满足线性和移不变性，则称该系统为线性移不变系统(LSI系统)。LSI系统应用非常广泛，并且研究人员已经开发出许多好用的工具来描述与分析它们。

LSI类系统可以被冲激响应完整的描述：向LSI系统输入一个单位冲激函数δ(n₁,n₂)，此时系统输出为h(n₁,n₂) 

则，称h(n₁,n₂)为LSI系统的冲击响应。对任意输入x(n₁,n₂)，有

x(n₁,n₂)** h(n₁,n₂)为x(n₁,n₂)与h(n₁,n₂)的2维卷积：

也就是说：一个LSI系统的输出图像，等于输入图像与该系统的冲激响应的2维卷积。简言之，只要知道了LSI系统的冲激响应，就能准确的得到任意输入信号通过系统后的输出。在使用一个LSI系统来处理图像时，或者说我们在做图像滤波时，实际上就是在用系统的冲激响应对输入图像中的像素做卷积运算。

3.二维傅里叶变换

傅里叶变换，让我们得以在频域描述任意维度的任意信号，以及在频域描述LSI系统中的任何运算。下面通过简单计算得到LSI系统在频域的响应函数，然后进一步得到该频域响应函数与LSI系统冲激响应函数之间的关系。

（1）LSI系统的频率响应

考虑一个冲激响应为h(n₁,n₂)的LSI系统，输入一个频率为ω₁和ω₂的复指数信号x(n₁,n₂)，输出为y(n₁,n₂)，如下图所示

由于LSI系统的输出等于输入信号与系统冲激响应的卷积，所以

因为输入信号 x ( n ₁ , n ₂ )为已知，作为线性系统可以将系数提出来。而将上式两个“连加号”中的项称为LSI系统在频点 ω ₁ 和 ω ₂ 处的频率响应(frequency response) H ( ω ₁ , ω ₂ )

（2）傅里叶变换公式

• 二维离散傅里叶变换：空域→频域

上式为傅里叶变换，它将图像x(n₁,n₂)从空域变换到频域X(ω₁,ω₂)，X(ω₁,ω₂)称为图像x(n₁,n₂)的频谱。

• 二维傅里叶逆变换：频域→空域

由傅里叶变换的定义及对LSI系统输出频率响应的分析可知，一个LSI系统的频率响应H(ω₁,ω₂)就是其冲激响应h(n₁,n₂)的傅里叶变换：

现在想一想，我们在图像滤波时设计的滤波核或模板，其实就是对这一LSI系统的冲激响应h(n₁,n₂)进行设计，不同的h(n₁,n₂)有同的频率响应特性H(ω₁,ω₂)，因此才会有不同的高通、低通滤波器。

4.卷积定理

对于一个LSI系统，输入图像为x(n₁,n₂)，输入图像频谱为X(ω₁,ω₂)，系统冲激响应为h(n₁,n₂)，系统频率响应为H(ω₁,ω₂)，则系统的空域输出为

由卷积定理可知，空域的卷积等于频域的乘积，则有

也就是说，输出图像的频谱Y(ω₁,ω₂)等于输入图像频谱与系统频率响应之积。当频率响应H(ω₁,ω₂)在频点H(0,0)=0时，输入图像在X(0,0)频点的能量无法通过，即Y(0,0)= X(0,0)×H(0,0)=0。而如果频率响应H(ω₁,ω₂)在某些频点值为1，则输入图像在这些频点的能量将全部通过系统。

由此可见，LSI系统的频率响应H(ω₁,ω₂)的曲线形状决定了哪些频率的能量能全部通过系统甚至被放大（H(ω₁,ω₂)≥1），哪些频率会被衰减（0<H(ω₁,ω₂)<1）或拒绝通过（H(ω₁,ω₂)=0）

5.图像频域滤波

图像中不同灰度级（或颜色）在空间上的分布，称为空域（spatial domain）。用x(n₁,n₂)表示图像在(n₁,n₂)点上的强度值。

图像中灰度级的变化的快慢，称为频域（frequency domain）。用X(ω₁,ω₂)表示图像在频率(ω₁,ω₂)处的强度值，因为图像是二维的，因此其频率变化也是二维的。

频域分析把图像分解为从低频到高频的频率成分。图像强度变化慢的区域只包含低频成分；强度值快速变化的区域产生高频成分。通过傅里叶变换或余弦变化可以清楚地显示图像的频率成分。图像是二维的，因此频率分两种，即垂直频率（垂直方向的变化ω₁）和水平频率（水平方向的变化ω₂）。

在频域分析的框架下，滤波器是一种放大图像中某些频段，同时滤掉（或减弱）其他频段的算子。低通滤波器（LPF, Low Pass Filter）就是消除高频部分，让低频分量通过；高通滤波器（HPF, High Pass Filter）就是消除低频部分，让高频分量通过。

之所以可以选择性的让某些频段通过，是因为图像滤波使用了逐个像素进行二维离散卷积的形式实现，而我们知道对空域信号的卷积相当于在频域的乘积。因此，滤波核的频率响应H(ω₁,ω₂)乘原始像素的频谱X(ω₁,ω₂)，相当于滤除了滤波核频谱较低位置的频率分量，而只有滤波和频谱较高区域的频率分量得以通过。

（1）低通滤波器

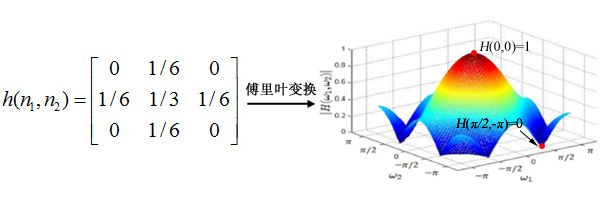
下面的h(n₁,n₂)为一个低通滤波器的滤波核，也就是冲激响应

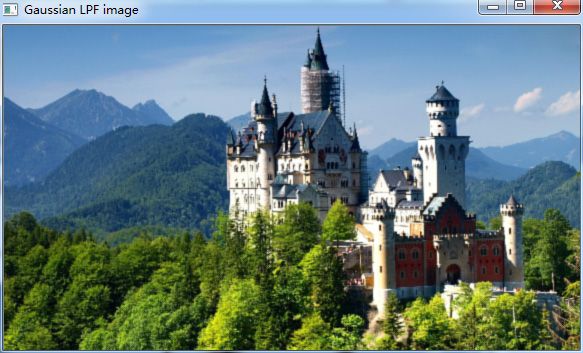
原图

低通滤波结果

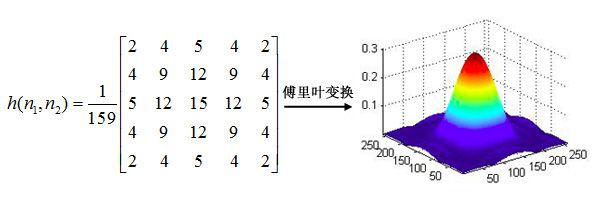
高斯低通滤波器

高斯滤波器是一种常见的低通滤波器，用于抑制服从正态分布的噪声非常有效。其滤波核中像素对应的权重（冲激响应h）与它到中心像素之间的距离成正比。

参数σ决定高斯函数曲线的宽度，即边缘像素所占比例的大小。σ越小曲线越窄，边缘像素的权重越低；反之，σ越大，曲线越宽，边缘像素所占权重越大。一维高斯分布如下图所示。

一维高斯分布

二维高斯分布：

一个5×5的高斯滤波器：

5×5的高斯滤波结果

无论是第一个低通滤波器例子还是高斯滤波的例子，从低通滤波结果可以看出，原始图像中的低频分量（图像的平缓部分）通过了滤波器，而高频分量（原图中边缘的部分）被抑制，整幅图像被平滑了，丢失了高频细节信息。

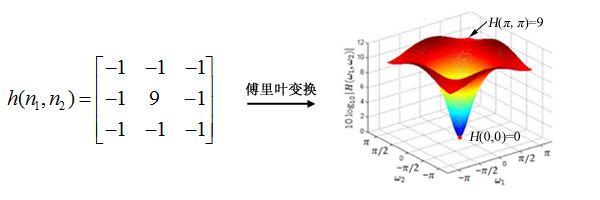
（2）高通滤波器

下面的h(n₁,n₂)为一个高通滤波器的滤波核

高通滤波结果

从高通滤波结果可以看出，原始图像中的高频分量（图像的边缘）被放大，而低频分量（原图中平缓的部分）被抑制。

（3）构造滤波器冲激响应的方法

以下代码使用C++和OpenCV编写，说明了如何自定义频域滤波器的冲激响应h(n₁,n₂)，并对输入图像进行滤波实验。

// open the image
cv::Mat image= cv::imread("f:\\images\\castle.jpg",1);//1：以彩色图读入
if(!image.data)
    return -1;

// image is resized for book printing
cv::resize(image, image, cv::Size(), 0.3, 0.3);

//建立图像缓存
Mat LPFimage,HPFimage;

//创建自定义结构元素-滤波核
float m_LPF[9] = {
		   0,   0.167,    0,
		 0.167, 0.333,  0.167,
		   0,   0.167,    0	
	         };
float m_HPF[9] = {
		   -1.0,   -1.0,    -1.0,
		   -1.0,     9,     -1.0,
		   -1.0,   -1.0,    -1.0	
	          };

//生成LPF滤波核
cv::Mat h_LPF(3,3,CV_32F,m_LPF); 

//生成HPF滤波核
cv::Mat h_HPF(3,3,CV_32F,m_HPF); 

//显示滤波核
int nr = h_LPF.rows;
int nl = h_LPF.cols;
for(int j = 0;j(j);
	for(int i = 0; i(j);
	for(int i = 0; i

转载请注明：iracer的CSDN博客 http://blog.csdn.net/iracer/article/details/49330533