K近邻算法:KNN
K K K 近邻 ( k N N kNN kNN) 算法是一种基本分类与回归方法,通俗的理解为给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的 k k k 个实例,这 k k k 个实例的多数属于某个类,就把该输入实例分为这个类。
- 经典描述
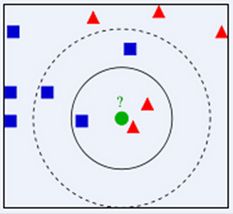
如下图,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形。如果 K = 3 K=3 K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果 K = 5 K=5 K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。因此也说明了 K N N KNN KNN 算法的结果很大程度取决于 K K K如何选择
2. 原理
在KNN中,通过计算对象间距离来作为各个对象之间的非相似性指标,一般使用欧氏距离或曼哈顿距离:
欧氏距离: d ( x , y ) = ∑ k = 1 n ( x k − y k ) 2 {\text{d}}(x,y) = \sqrt {\sum\limits_{k = 1}^n {{{({x_k} - {y_{_k}})}^2}} } d(x,y)=k=1∑n(xk−yk)2
曼哈顿距离: d ( x , y ) = ∑ k = 1 n ∣ x k − y k ∣ {\text{d}}(x,y) = \sqrt {\sum\limits_{k = 1}^n {|{x_k} - {y_{_k}}|} } d(x,y)=k=1∑n∣xk−yk∣
假设有一个带有标签的样本数据集,其中包含每条数据与所属分类的对应关系。输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,求 k 个数据中出现次数最多的分类标签作为新数据的分类。
3. K K K值确定
K N N KNN KNN 算法中只有唯一的一个超参数 K K K,很明显 K K K 值的选择对最终算法的预测结果有着至关重要的影响。 K N N KNN KNN 算法中只有唯一的一个超参数 K K K,很明显 K K K 值的选择对最终算法的预测结果有着至关重要的影响。
如果选择的 K K K 值比较少,相当于使用较小领域中的训练样本对实例进行预测。这时,算法的近似误差会减小,因为只有与输入实例相近的训练样本才能对预测结果起作用。但它也有明显的缺点,算法的估计误差会偏大,预测的结果会对近邻点十分敏感,也就是说如果近邻点是噪声点的话,预测就会出错。总之, K K K 值太小很容易使 K N N KNN KNN 算法产生过拟合。同理,如果 K K K 值选的比较大,距离较远的训练样本都会对实例的预测结果产生影响。同时,模型相对比较鲁棒,不会因个别噪声点对最终的预测产生影响。但缺点也十分明显,算法的近似误差会偏大,距离较远的点(与预测实例不相似)同样会对预测产生作用,最终使预测结果产生较大偏差。此时,相当于模型发生欠拟合。
因此,在工程实践中,我们一般采用交叉验证的方式选取 K K K 值。从上面的分析也可知道,一般 K K K 值取得比较小。我们会在较小的范围内选取 K K K 值,同时将测试集上准确率最高的那一个确定为最终的算法超参数 K K K。
4. 开发流程
1. 计算新数据与样本数据集中每条数据的距离。
2. 对求得的所有距离进行排序(从小到大,越小表示越相似)。
3. 取前 k (k <= 20 ) 个样本数据对应的分类标签。
5. 优缺点
优点:
1. 理论成熟,思想简单,既可以用来做分类也可以用来做回归
2. 可用于非线性分类
3. 训练时间复杂度为O(n)
4. 对数据没有假设,准确度高,对outlier不敏感
5. KNN是一种在线技术,新数据可以直接加入数据集而不必进行重新训练
6. KNN理论简单,容易实现
缺点:
1. 样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少)效果差
2. 需要大量内存
3. 对于样本容量大的数据集计算量比较大(体现在距离计算上)
4. 样本不平衡时,预测偏差比较大。如:某一类的样本比较少,而其它类样本比较多
5. KNN每一次分类都会重新进行一次全局运算
6. k值大小的选择没有理论选择最优,往往是结合K-折交叉验证得到最优k值选择
6. 主要应用
文本分类、模式识别、聚类分析,多分类领域
7. 约会经典案例
海伦使用约会网站寻找约会对象。经过一段时间之后,她发现曾交往过三种类型的人: 不喜欢的人,魅力一般的人,极具魅力的人
她希望: 1. 工作日与魅力一般的人约会 2. 周末与极具魅力的人约会 3. 不喜欢的人则直接排除掉
- 搜集数据
海伦把这些约会对象的数据存放在文本文件 datingTestSet2.txt 中,总共有 1000 行。海伦约会的对象主要包含以下 3 种特征:
每年获得的飞行常客里程数
玩视频游戏所耗时间百分比
每周消费的冰淇淋公升数
文本文件数据格式如下:
40920 8.326976 0.953952 3
14488 7.153469 1.673904 2
26052 1.441871 0.805124 1
75136 13.147394 0.428964 1
38344 1.669788 0.134296 1
- 准备数据
def file2matrix(filename):
fr = open(filename) #打开数据集
arrayOLines = fr.readlines()
numberOfLines = len(arrayOLines) #获取数据集行数
returnMat = zeros((numberOfLines, 3)) #创建空矩阵
classLabelVector = []
index = 0
for line in arrayOLines:
line = line.strip()
listFromLine = line.split('\t') #获取每列的属性数据
returnMat[index, :] = listFromLine[0: 3] #将前三列数据存入矩阵中
classLabelVector.append(int(listFromLine[-1])) #获取最后一列数据
index += 1
return returnMat, classLabelVector- 数据归一化
归一化特征值就是要把需要处理的数据经过处理后限制在一定范围内,主要是为了消除特征之间量级不同导致的影响。我们一般使用最大最小值规格化的方法:
y = x − x min x max − x min y = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} y=xmax−xminx−xmin
例:某公司工资水平在12000~98000之间,映射到(0, 1),某员工工资为73600,则:
y = 73600 − 12000 98000 − 12000 = 0.716 y = \frac{{73600 - 12000}}{{98000 - 12000}} = 0.716 y=98000−1200073600−12000=0.716
def autoNorm(dataSet):
minVals = dataSet.min(0) #返回矩阵每一列的最小值
maxVals = dataSet.max(0) #返回矩阵每一列的最大值
ranges = maxVals - minVals #获取范围
m = dataSet.shape[0]
normDataSet = dataSet - tile(minVals, (m, 1)) #生成与最小值之差组成的矩阵
normDataSet = normDataSet/tile(ranges, (m, 1)) #归一化
return normDataSet, ranges, minVals- KNN算法
对于数据集中的数据:
1. 计算目标的数据与该数据的距离
2. 距离排序:从小到大
3. 选取前K个最短距离
4. 选取这K个中最多的类别
5. 返回该类别来作为目标数据点的预测值
def classify(input, dataSet, label, k):
#1. 计算目标的数据与该数据的距离
dataSize = dataSet.shape[0]
diff = tile(input, (dataSize, 1)) - dataSet
sqdiff = diff ** 2
squareDist = sum(sqdiff, axis=1) #行向量分别相加
dist = squareDist ** 0.5 #计算欧式距离
#2. 排序
sortedDistIndex = argsort(dist)
#3. 选取前K个最短距离
classCount = {}
for i in range(k):
voteLabel = label[sortedDistIndex[i]]
classCount[voteLabel] = classCount.get(voteLabel, 0) + 1 #选取前K个最小距离
#4. 选取这K个中最多的类别
maxCount = 0
for key, value in classCount.items(): #选取出现的类别次数最多的类别
if value > maxCount:
maxCount = value
classes = key
#5. 返回该类别来作为目标数据点的预测值
return classes- 测试与结果
if __name__ == '__main__':
resultList = [u'不喜欢', u'魅力一般', u'极具魅力']
percentTats = float(input(u"玩视频游戏所耗时间百分比:"))
ffMiles = float(input(u"每年获得的飞行常客里程数:"))
iceCream = float(input(u"每周消费的冰淇淋公升数:"))
datingDataMat, datingLabels = file2matrix('C:\\Users\\John\\Desktop\\DataBooks\\MachineLearning\\Ch02\\datingTestSet2.txt')#导入并处理数据
normMat, ranges, minVals = autoNorm(datingDataMat) #数据归一化
inArr = array([ffMiles, percentTats, iceCream])
classifierResult = classify((inArr-minVals)/ranges, normMat, datingLabels, 3) #分类
print("对此人感觉: ", resultList[classifierResult - 1])
海伦最后能根据输入的条件来预测对这个约会对象的感觉,从而决定是否或者何时约会。这就是一个完整的KNN流程。
-
代码分析
K近邻代码 -
s k l e a r n sklearn sklearn实践
scikit-learn(简称sklearn)是目前最受欢迎,也是功能最强大的一个用于机器学习的 P y t h o n Python Python 库。它广泛地支持各种分类、聚类以及回归分析方法,由于其强大的功能、优异的拓展性以及易用性,目前受到了很多数据科学从业者的欢迎,也是业界相当著名的一个开源项目之一。下面我们使用 s k l e a r n sklearn sklearn 完成 K N N KNN KNN 的分类,具体过程我就不仔细讲(这里我就不使用上面的数据,因为是之前写的,数据已经找不到,所以这里包括后面的算法全部使用 i r i s ( 鸢 尾 花 ) iris(鸢尾花) iris(鸢尾花) 的数据进行分析):
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
iris = datasets.load_iris() # 加载iris数据集
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
clf = KNeighborsClassifier(n_neighbors=15, weights="distance")
clf.fit(X_train, y_train) # 模型训练
ans = clf.predict(X_test) # 结果预测
# 计算准确率
cnt = 0
for i in range(len(y_test)):
if ans[i] - y_test[i] < 1e-1:
cnt += 1
print("准确率: ", (cnt * 100.0 / len(y_test)), "%")分类结果如下:
准确率: 100.0 %