评分卡建模
数据:
"拍拍贷"提供的数据包括信用违约标签(因变量)、建模所需的基础与加工字段(自变量)、相关用户的网络行为原始数据,数据字段已经做脱敏处理。本次实战采用的是初赛数据,包括3万条训练集和2万条测试集。数据文档包括:
Master:每一行代表一个样本(一笔成功成交借款),每个样本包含200多个各类字段。
Log_Info:借款人的登陆信息,每个样本含多条数据。
Userupdate_Info:借款人修改信息,每个样本多条数据。
一.探索性数据分析
数据清洗工作,对缺失值,异常值进行了处理,
特征工程,分为特征转换和特征衍生。主要做了以下工作:
Master数据:地理位置信息的处理(省份,城市),以及对排序特征,periods特征的交叉组合等。
Log_Info数据:衍生出"累计登陆次数",“登录时间的平均间隔”,“最近一次的登录时间距离成交时间差” 等特征。
Userupdate_Info数据:衍生出"最近的修改时间距离成交时间差",“修改信息的总次数”, "每种信息修改的次数"等特征。
二.特征筛选工作:
1因为评分卡对数据质量要求较高,首先建立xgboost模型对变量进行了初步筛选。
2然后对特征进行了卡方分箱,根据分箱结果计算了各个特征的IV值,剔除了IV值小于0.02的特征。
3逻辑回归作为一种线性模型,其基础假设是:自变量之间应相互独立。当两变量间的相关系数大于阈值时(一般阈值设为0.6),剔除IV值较低的变量;
4. 当出现多重共线性时,变量之间的联动关系会导致估计标准差偏大,置信区间变宽。这就会产生一个常见的现象,LR中变量系数出现正负号不一致。
三.建模工作:
WOE转换
样本权重
分数校准
模型保存(Save Model)
四. 模型评估
1. 稳定性(Stability)-PSI
2. 区分度(Discrimination)-
3. 排序性(Ranking)
4. 拟合度(Goodness of Fit)
一.探索性数据分析:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
log_data=pd.read_csv(folder+'PPD_LogInfo_3_1_Training_Set.csv',encoding='GBK')
update_log=pd.read_csv(folder+'PPD_Userupdate_Info_3_1_Training_Set.csv',encoding='GBK')
train=pd.read_csv(folder+'PPD_Training_Master_GBK_3_1_Training_Set.csv',encoding='GBK')
Mater数据包含约30000个样本,200多个字段
# 样本的好坏比
train.target.value_counts()
0 27802
1 2198
Name: target, dtype: int64
好坏比约11:1,属于不平衡数据集.
处理缺失值
miss=pd.DataFrame()
dd=[]
cc=[]
rr=[]
for i in train.columns:
d=len(train)-train[i].count()
r=(d/len(train))*100
dd.append(i)
cc.append(d)
rr.append(r)
miss['字段名为']=dd
miss['缺失值数量']=cc
miss['缺失数量占比']=rr
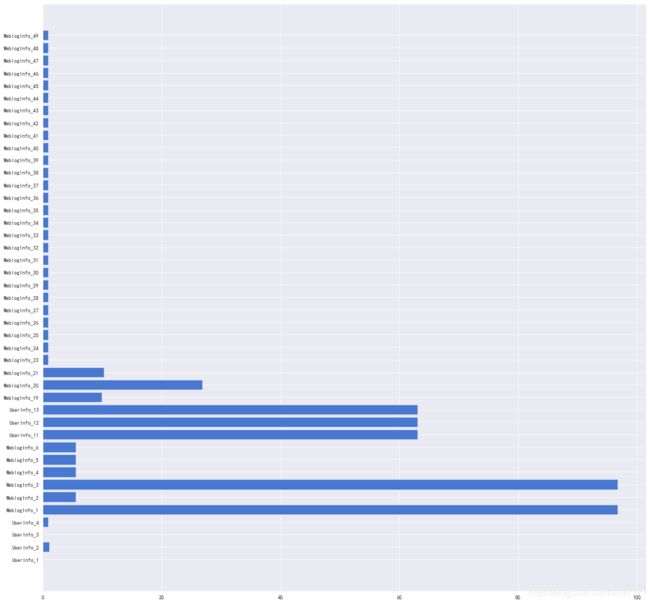
plt.figure(figsize=(20,20))
plt.barh(miss[miss['缺失数量占比']>0].字段名为,miss[miss['缺失数量占比']>0].缺失数量占比)
将缺失率90%以上的变量删除
train=train.drop(['WeblogInfo_1','WeblogInfo_3'],axis=1)
单一值占比
unique={}
for var in train.drop(['Idx','ListingInfo','target'],axis=1).columns:
most=train[var].value_counts().iloc[0]
most_value=train[var].value_counts().index[0]
most_ratio=most/30000
unique[var]=[most,most_value,most_ratio]
如果单一值占比多数值与少数值的坏样本率有显著差别,则需保留该字段。
del_cols2={}
for v in unique:
if unique[v][2]>0.9:
most_bad_ratio=train[train[v]==unique[v][1]].target.sum()/train[train[v]==unique[v][1]].target.count()
not_most_bad_ratio=train[train[v]!=unique[v][1]].target.sum()/train[train[v]!=unique[v][1]].target.count()
del_cols2[v]=[most_bad_ratio,not_most_bad_ratio]
观察发现有显著差别字段的单一值为-1即缺失值,且未缺失的样本占比仅有1%,因此可删除单一值占比超过90%的字段
#删除单一值占比超过0.9的变量
for v in unique:
if unique[v][2]>0.9:
del_cols.append(v)
train_after_unique=train.drop(del_cols,axis=1)
中文特征处理
#计算4个城市特征的非重复项计数,观察是否有数据异常
for col in ['UserInfo_2','UserInfo_4','UserInfo_8','UserInfo_20']:
print('{}:{}'.format(col,train[col].nunique()))
print('\t')
UserInfo_8相对其他特征nunique较大,发现有些城市有"市",有些没有,需要做一下格式转换,去掉字符串后缀"市".
train['UserInfo_8']=[s[:-1] if s.find('市')>0 else s[:] for s in train.UserInfo_8]
衍生特征
log_data衍生的变量
累计登录次数
登录时间的平均间隔
最近一次的登录时间距离成交时间差
# 累计登录次数
log_cnt = log_data.groupby('Idx',as_index=False).LogInfo3.count().rename(columns={'LogInfo3':'log_cnt'})
# 最近一次的登录时间距离当前时间差
log_data['Listinginfo1']=pd.to_datetime(log_data.Listinginfo1)
log_data['LogInfo3'] = pd.to_datetime(log_data.LogInfo3)
time_log_span = log_data.groupby('Idx',as_index=False).agg({'Listinginfo1':np.max,
'LogInfo3':np.max})
time_log_span['log_timespan'] = time_log_span['Listinginfo1']-time_log_span['LogInfo3']
time_log_span['log_timespan'] = time_log_span['log_timespan'].map(lambda x:str(x))
time_log_span['log_timespan'] = time_log_span['log_timespan'].map(lambda x:int(x[:x.find('d')]))
time_log_span= time_log_span[['Idx','log_timespan']]
# 登录时间的平均时间间隔
temp = log_data.sort_values(by=['Idx','LogInfo3'],ascending=['True','True'])
temp['LogInfo4'] = temp.groupby('Idx')['LogInfo3'].apply(lambda x:x.shift(1))
temp['time_span'] = temp['LogInfo3']-temp['LogInfo4']
temp['time_span'] = temp['time_span'].map(lambda x:str(x))
temp = temp.replace({'time_span':{'NaT':'0 days 00:00:00'}})
temp['time_span'] = temp['time_span'].map(lambda x:int(x[:x.find('d')]))
avg_log_timespan = temp.groupby('Idx',as_index=False).time_span.mean().rename(columns={'time_span':'avg_log_timespan'})
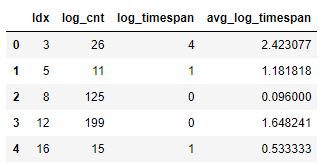
#将三个衍生特征组合成一张表
log_info = pd.merge(log_cnt,time_log_span,how='left',on='Idx')
log_info = pd.merge(log_info,avg_log_timespan,how='left',on='Idx')
log_info.head()
# 时间格式的转换
update_log['ListingInfo1'] = pd.to_datetime(update_log['ListingInfo1'])
update_log['UserupdateInfo2'] = pd.to_datetime(update_log['UserupdateInfo2'])
# 计算时间差
time_span = update_log.groupby('Idx',as_index=False).agg({'UserupdateInfo2':np.max,'ListingInfo1':np.max})
time_span['update_timespan'] = time_span['ListingInfo1']-time_span['UserupdateInfo2']
time_span['update_timespan'] = time_span['update_timespan'].map(lambda x:str(x))
time_span['update_timespan'] = time_span['update_timespan'].map(lambda x:int(x[:x.find('d')]))
time_span = time_span[['Idx','update_timespan']]
# 修改信息的总次数,按照日期修改的次数的衍生
update_cnt = update_log.groupby('Idx',as_index=False).agg({'UserupdateInfo2':pd.Series.nunique,
'ListingInfo1':pd.Series.count}).\
rename(columns={'UserupdateInfo2':'update_time_cnt',
'ListingInfo1':'update_all_cnt'})
update_cnt.head()
特征筛选
由于评分卡模型使用逻辑回归算法,对数据质量要求较高,且在风控领域稳定压倒一切,因此需要对数据的稳定性进行判断。由于数据中没有分时间窗口,因此暂不进行对单个变量PSI的检验。
先将衍生特征与用户属性特征进行合并
train=train.merge(update_info,on='Idx',how='left')
train=train.merge(log_info,on='Idx',how='left')
train.shape #30000 rows × 155 columns
共有155列特征,用众数填充缺失值
for col in train.columns:
train[col].fillna(train[col].mode()[0],inplace=True)
卡方分箱
对处理过的特征进行卡方分箱,将缺失值单独作为一箱
import scorecardpy as sc
bins = sc.woebin(train, y="target",bin_num_limit=7,method='chimerge')
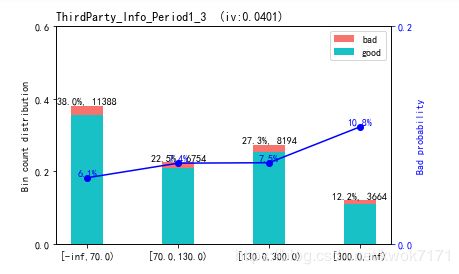
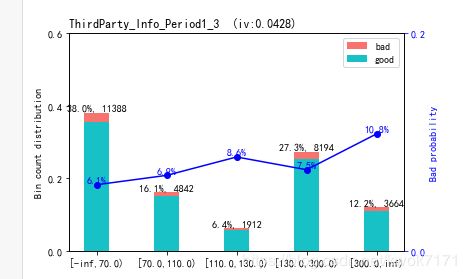
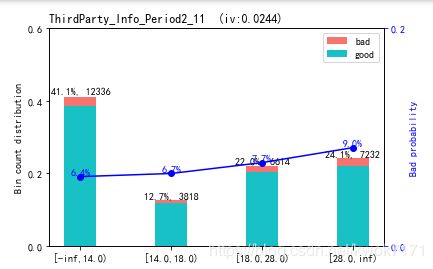
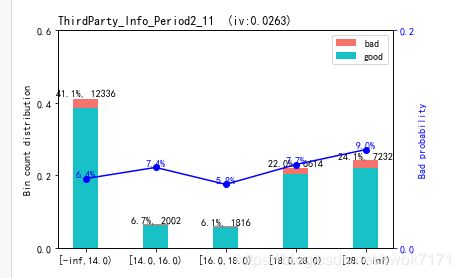
数值型变量的分箱结果尽量保持坏样本率的单调性,对不符合单调性的箱进行合并,下图左边为修改过的分箱结果,右边为修改前的分分箱结果。
IV值筛选,删除IV值小于0.02以下的变量
lowiv_cols={}
highiv_cols={}
for i in bins:
if bins[i].total_iv [0]>=0.02:
highiv_cols[i]=bins[i].total_iv [0]
else:
lowiv_cols[i]=bins[i].total_iv [0]
woe转换
train_woe = sc.woebin_ply(trains, bins)
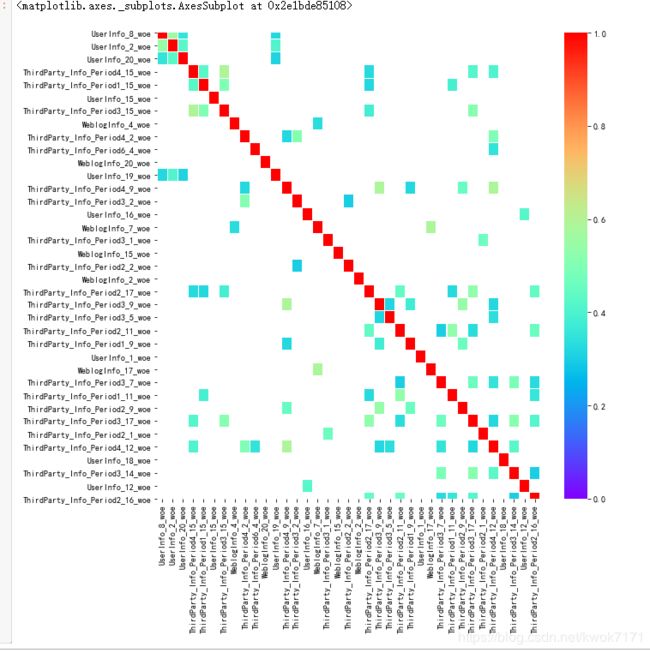
检查WOE编码后的变量的两两线性相关性
var_IV_sorted = high_cols.copy()
removed_var = []
roh_thresould = 0.6
for i in range(len(var_IV_sorted)-1):
x1 = var_IV_sorted[i]+"_woe"
for j in range(i+1,len(var_IV_sorted)):
x2 = var_IV_sorted[j] + "_woe"
roh = np.corrcoef([all_woe[x1], all_woe[x2]])[0, 1]
if abs(roh) >= roh_thresould:
print('the correlation coeffient between {0} and {1} is {2}'.format(x1, x2, str(roh)))
if highiv_cols_sort[var_IV_sorted[i]] > highiv_cols_sort[var_IV_sorted[i]]:
removed_var.append(var_IV_sorted[j])
else:
removed_var.append(var_IV_sorted[i])
共移除了70个特征
移除之后的线性相关性:
f, ax = plt.subplots(figsize = (10, 10))
sns.heatmap(all_woe[high_cols3].corr(), linewidths = 0.05, ax = ax, vmax=1, vmin=-1,
cmap='rainbow',center=None, robust=False, annot=False,mask=all_woe[high_cols3].corr()<0.3)
检查变量之间的多重共线性
## 每轮循环中计算各个变量的VIF,并删除VIF>threshold 的变量
def vif(X, thres=10.0):
col = list(range(X.shape[1]))
dropped = True
while dropped:
dropped = False
vif = [variance_inflation_factor(X.iloc[:,col].values, ix)
for ix in range(X.iloc[:,col].shape[1])]
maxvif = max(vif)
maxix = vif.index(maxvif)
if maxvif > thres:
del col[maxix]
print('delete=',X_train.columns[col[maxix]],' ', 'vif=',maxvif )
dropped = True
print('Remain Variables:', list(X.columns[col]))
print('VIF:', vif)
return list(X.columns[col])
high_cols4=vif(all_woe[high_cols3])
变量的方差膨胀因子都小于10,因此无需删除变量。
VIF: [1.546138236927055, 1.7367083348951569, 1.3198558444704924, 2.008431474409975, 1.65369907960681, 1.0442488892524127, 2.107884876714126, 1.25394020850467, 1.7361649402693806, 1.264673367131633, 1.0360964085205682, 1.2675604455511582, 2.3943709908755815, 1.5553863383472155, 1.2647293473087204, 1.7373278326048085, 1.5386811797657178, 1.147621666271261, 1.1489577482378157, 1.0700749370393328, 1.7818208988427156, 2.0259339358880855, 1.4108611630579697, 1.847910055479312, 1.4229334395485966, 1.091939115911497, 1.555010482459932, 1.6442512776885183, 1.7685647717683375, 1.6935427789210498, 2.3970670883123257, 1.2977784794527287, 2.6746159843650217, 1.0259757671025698, 1.8137646152549658, 1.382924938424076, 1.5911509813606357]
评分卡模型入模变量一般不超过20个,通过xgboost对变量再进行一次筛选
from xgboost import XGBClassifier
clf = XGBClassifier(
n_estimators=10,#三十棵树
learning_rate =0.1,
max_depth=3,
min_child_weight=2,
gamma=0.3,
subsample=0.8,
colsample_bytree=0.8,
objective= 'binary:logistic',
nthread=12,
reg_lambda=1,
seed=27)
model_sklearn=clf.fit(train_X, train_y,eval_set=[(train_X, train_y),(test_x, test_y)],
eval_metric='auc')
from xgboost import plot_importance
plot_importance(clf)
plt.show()

最终确定43个入模变量,有点多,一般评分卡要求入模变量20个以下,可以根据数据源分别建立模型,最后再进行汇总,如将第三方数据,内部数据,APP数据等分别建模,最后进行汇总,解决这个问题。
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(penalty='l1', C=0.9, solver='saga', n_jobs=-1,max_iter=2000)
lr.fit(X_train, y_train)
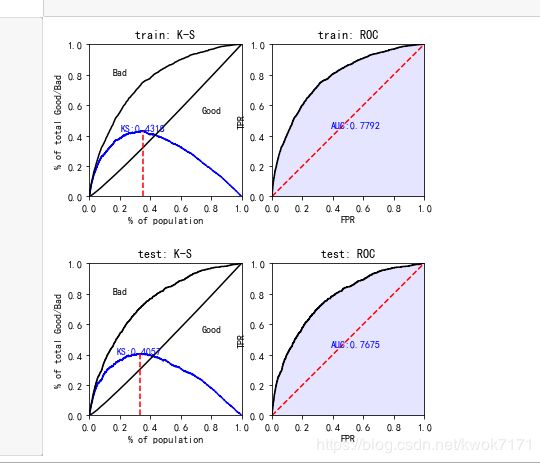
#ks和roc曲线
train_perf = sc.perf_eva(y_train, train_pred, title = "train")
test_perf = sc.perf_eva(y_test, test_pred, title = "test")
# 转化为分数形式
card = sc.scorecard(bins, lr, X_train.columns)
# credit score
train_score = sc.scorecard_ply(trains, card, print_step=0)
test_score = sc.scorecard_ply(tests, card, print_step=0)
#模型的稳定性PSI
sc.perf_psi(
score = {'train':train_score, 'test':test_score},
label = {'train':y_train, 'test':y_test}
)
#测试集分数的分布
fig,ax=plt.subplots()
ax.hist(test_woe[test_woe['target']==1].score,bins=12,histtype="stepfilled",alpha=0.6,label="违约",color='red')
ax.hist(test_woe[test_woe['target']==0].score,bins=12,histtype="stepfilled",alpha=0.6,label="未违约",color='lavender')
ax.legend()
#ax.set_xticks(np.arange(0,721,60))
#ax.set_xlim(0,720)
#ax.set_yticks(np.arange(0,21,4))
plt.show()
模型稳定性:PSI小于0.01,表示在训练集和测试集上比较稳定。
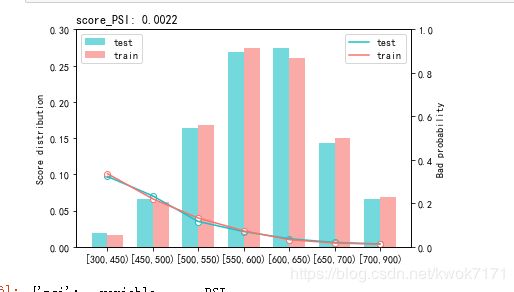
用户分数分布图


分数分布表

最后我们用statsmodels建立一次模型,观察一下变量是否显著以及变量的系数
import statsmodels.api as sm
lr2=sm.Logit(y_train,X_train)
result=lr2.fit()
print(result.summary2())
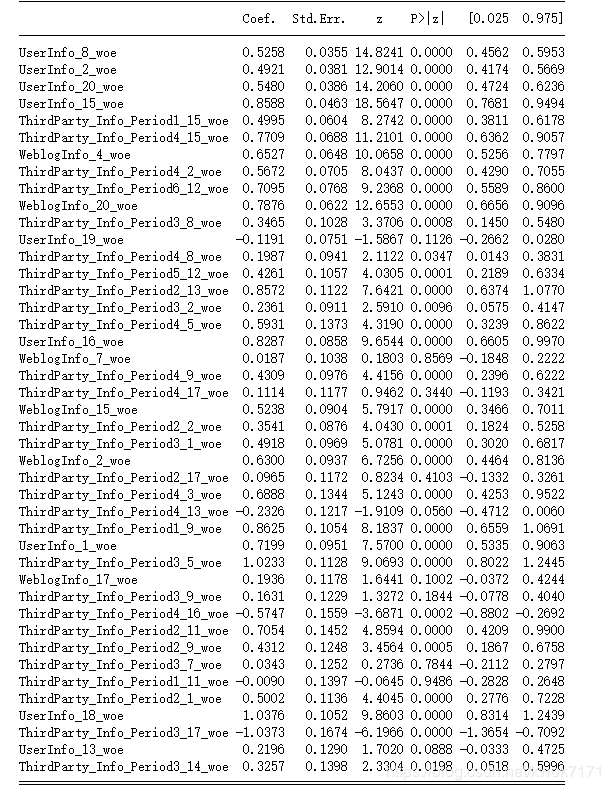
有些变量的P值过高,有的变量系数符号为负,说明仍有线性相关性或多重共线性的影响,可以通过单独用该变量做一元逻辑回归模型检验,如果需要可以剔除该变量或者通过调整逻辑回归的L2范数来调整。