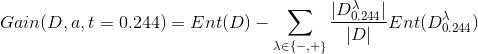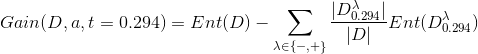机器学习笔记（5）——C4.5决策树中的连续值处理和Python实现

 

在ID3决策树算法中，我们实现了基于离散属性的决策树构造。C4.5决策树在划分属性选择、连续值、缺失值、剪枝等几方面做了改进，内容较多，今天我们专门讨论连续值的处理和Python实现。

1. 连续属性离散化

C4.5算法中策略是采用二分法将连续属性离散化处理：假定样本集D的连续属性有n个不同的取值，对这些值从小到大排序，得到属性值的集合。把区间的中位点作为候选划分点，于是得到包含n-1个元素的划分点集合

基于每个划分点t，可将样本集D分为子集和，其中中包含属性上不大于t的样本，包含属性上大于t的样本。

对于每个划分点t，按如下公式计算其信息增益值，然后选择使信息增益值最大的划分点进行样本集合的划分。

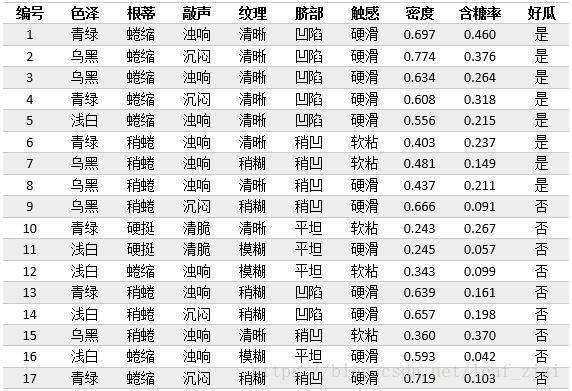
在ID3算法中的西瓜数据集中增加两个连续属性“密度”和“含糖率”，下面我们计算属性“密度”的信息增益。

从数据可以看出，17个样本的密度属性值均不同，因此该属性的候选划分点集合由16个值组成：

                                       

                                       

                                       

                                       

                                       

                                       

所有划分点的信息增益均可按上述方法计算得出，最优划分点为0.381，对应的信息增益为0.263。我们分别按照离散值和连续值的信息增益计算方法，计算出每个属性的信息增益，从而选择最优划分属性，构造决策树。

需要注意的是：当前节点划分属性为连续属性，该属性还可作为其后代节点的划分属性。

2. Python实现

在ID3决策树算法的基础上，我们需要新增或修改一些方法，以便可以处理连续值。

• 新增一个划分数据集的方法

# 划分数据集, axis:按第几个特征划分, value:划分特征的值, LorR: value值左侧（小于）或右侧（大于）的数据集
def splitDataSet_c(dataSet, axis, value, LorR='L'):
    retDataSet = []
    featVec = []
    if LorR == 'L':
        for featVec in dataSet:
            if float(featVec[axis]) < value:
                retDataSet.append(featVec)
    else:
        for featVec in dataSet:
            if float(featVec[axis]) > value:
                retDataSet.append(featVec)
    return retDataSet

• 修改原来的最优划分属性选择方法，在其中增加连续属性的分支

# 选择最好的数据集划分方式
def chooseBestFeatureToSplit_c(dataSet, labelProperty):
    numFeatures = len(labelProperty)  # 特征数
    baseEntropy = calcShannonEnt(dataSet)  # 计算根节点的信息熵
    bestInfoGain = 0.0
    bestFeature = -1
    bestPartValue = None  # 连续的特征值，最佳划分值
    for i in range(numFeatures):  # 对每个特征循环
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)  # 该特征包含的所有值
        newEntropy = 0.0
        bestPartValuei = None
        if labelProperty[i] == 0:  # 对离散的特征
            for value in uniqueVals:  # 对每个特征值，划分数据集, 计算各子集的信息熵
                subDataSet = splitDataSet(dataSet, i, value)
                prob = len(subDataSet) / float(len(dataSet))
                newEntropy += prob * calcShannonEnt(subDataSet)
        else:  # 对连续的特征
            sortedUniqueVals = list(uniqueVals)  # 对特征值排序
            sortedUniqueVals.sort()
            listPartition = []
            minEntropy = inf
            for j in range(len(sortedUniqueVals) - 1):  # 计算划分点
                partValue = (float(sortedUniqueVals[j]) + float(
                    sortedUniqueVals[j + 1])) / 2
                # 对每个划分点，计算信息熵
                dataSetLeft = splitDataSet_c(dataSet, i, partValue, 'L')
                dataSetRight = splitDataSet_c(dataSet, i, partValue, 'R')
                probLeft = len(dataSetLeft) / float(len(dataSet))
                probRight = len(dataSetRight) / float(len(dataSet))
                Entropy = probLeft * calcShannonEnt(
                    dataSetLeft) + probRight * calcShannonEnt(dataSetRight)
                if Entropy < minEntropy:  # 取最小的信息熵
                    minEntropy = Entropy
                    bestPartValuei = partValue
            newEntropy = minEntropy
        infoGain = baseEntropy - newEntropy  # 计算信息增益
        if infoGain > bestInfoGain:  # 取最大的信息增益对应的特征
            bestInfoGain = infoGain
            bestFeature = i
            bestPartValue = bestPartValuei
    return bestFeature, bestPartValue

• 修改原来的决策树构建方法 

# 创建树, 样本集 特征 特征属性（0 离散， 1 连续）
def createTree_c(dataSet, labels, labelProperty):
    # print dataSet, labels, labelProperty
    classList = [example[-1] for example in dataSet]  # 类别向量
    if classList.count(classList[0]) == len(classList):  # 如果只有一个类别，返回
        return classList[0]
    if len(dataSet[0]) == 1:  # 如果所有特征都被遍历完了，返回出现次数最多的类别
        return majorityCnt(classList)
    bestFeat, bestPartValue = chooseBestFeatureToSplit_c(dataSet,
                                                        labelProperty)  # 最优分类特征的索引
    if bestFeat == -1:  # 如果无法选出最优分类特征，返回出现次数最多的类别
        return majorityCnt(classList)
    if labelProperty[bestFeat] == 0:  # 对离散的特征
        bestFeatLabel = labels[bestFeat]
        myTree = {bestFeatLabel: {}}
        labelsNew = copy.copy(labels)
        labelPropertyNew = copy.copy(labelProperty)
        del (labelsNew[bestFeat])  # 已经选择的特征不再参与分类
        del (labelPropertyNew[bestFeat])
        featValues = [example[bestFeat] for example in dataSet]
        uniqueValue = set(featValues)  # 该特征包含的所有值
        for value in uniqueValue:  # 对每个特征值，递归构建树
            subLabels = labelsNew[:]
            subLabelProperty = labelPropertyNew[:]
            myTree[bestFeatLabel][value] = createTree_c(
                splitDataSet(dataSet, bestFeat, value), subLabels,
                subLabelProperty)
    else:  # 对连续的特征，不删除该特征，分别构建左子树和右子树
        bestFeatLabel = labels[bestFeat] + '<' + str(bestPartValue)
        myTree = {bestFeatLabel: {}}
        subLabels = labels[:]
        subLabelProperty = labelProperty[:]
        # 构建左子树
        valueLeft = '是'
        myTree[bestFeatLabel][valueLeft] = createTree_c(
            splitDataSet_c(dataSet, bestFeat, bestPartValue, 'L'), subLabels,
            subLabelProperty)
        # 构建右子树
        valueRight = '否'
        myTree[bestFeatLabel][valueRight] = createTree_c(
            splitDataSet_c(dataSet, bestFeat, bestPartValue, 'R'), subLabels,
            subLabelProperty)
    return myTree

• 修改原来的测试方法

# 测试算法
def classify_c(inputTree, featLabels, featLabelProperties, testVec):
    firstStr = inputTree.keys()[0]  # 根节点
    firstLabel = firstStr
    lessIndex = str(firstStr).find('<')
    if lessIndex > -1:  # 如果是连续型的特征
        firstLabel = str(firstStr)[:lessIndex]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstLabel)  # 跟节点对应的特征
    classLabel = None
    for key in secondDict.keys():  # 对每个分支循环
        if featLabelProperties[featIndex] == 0:  # 离散的特征
            if testVec[featIndex] == key:  # 测试样本进入某个分支
                if type(secondDict[key]).__name__ == 'dict':  # 该分支不是叶子节点，递归
                    classLabel = classify_c(secondDict[key], featLabels,
                                           featLabelProperties, testVec)
                else:  # 如果是叶子， 返回结果
                    classLabel = secondDict[key]
        else:
            partValue = float(str(firstStr)[lessIndex + 1:])
            if testVec[featIndex] < partValue:  # 进入左子树
                if type(secondDict['是']).__name__ == 'dict':  # 该分支不是叶子节点，递归
                    classLabel = classify_c(secondDict['是'], featLabels,
                                           featLabelProperties, testVec)
                else:  # 如果是叶子， 返回结果
                    classLabel = secondDict['是']
            else:
                if type(secondDict['否']).__name__ == 'dict':  # 该分支不是叶子节点，递归
                    classLabel = classify_c(secondDict['否'], featLabels,
                                           featLabelProperties, testVec)
                else:  # 如果是叶子， 返回结果
                    classLabel = secondDict['否']

    return classLabel

3. 绘制决策树并测试数据

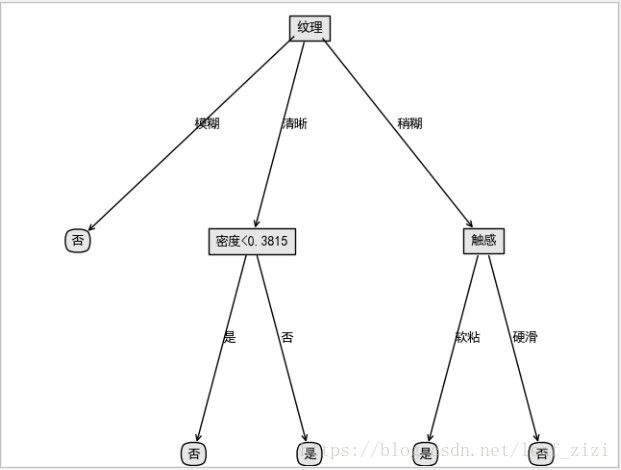
 我们利用上面的西瓜数据，绘制一个决策树。

fr = open(r'D:\Projects\PyProject\DecisionTree\watermalon3.0.txt')

listWm = [inst.strip().split('\t') for inst in fr.readlines()]
labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度', '含糖率']
labelProperties = [0, 0, 0, 0, 0, 0, 1, 1]  # 属性的类型，0表示离散，1表示连续
Trees = trees.createTree_c(listWm, labels, labelProperties)

print(json.dumps(Trees, encoding="cp936", ensure_ascii=False))

treePlotter.createPlot(Trees)

返回的决策树数据：{"纹理": {"模糊": "否", "清晰": {"密度<0.3815": {"是": "否", "否": "是"}}, "稍糊": {"触感": {"软粘": "是", "硬滑": "否"}}}}

 再用一条测试数据测试一下算法，看是否能得到正确的分类。

labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度', '含糖率']
labelProperties = [0, 0, 0, 0, 0, 0, 1, 1]
testData = ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.585, 0.002]
testClass = trees.classify_c(Trees, labels, labelProperties, testData)
print(json.dumps(testClass, encoding="cp936", ensure_ascii=False))

测试返回的结果是好瓜，从构造的树可以看出该数据进入纹理清晰，密度大于0.3815的分支，是正确的。

---

代码资源下载地址（留言回复可能不及时，请您自行下载）：

https://download.csdn.net/download/leaf_zizi/10867159

---

参考：

周志华《机器学习》

Peter Harrington 《机器学习实战》