Matlab 仿真（7，4）汉明码 传输误码率

汉明（7，4）码，传输7bits，其中4bits是信息，3bits是校验码

下面的程序是仿真汉明（7，4）码的编码，传输，解码的过程并统计误码率，希望对大家有所帮助。

% 产生信息序列，1000000个码 0/1

N = 1000000

for i=1:N
    if rand <.5
        s(i)=0;
    else
        s(i)=1;
    end
end

% 产生3bits的校验码
source = reshape(s,N/4,[]);
 for i = 1:N/4
     source(i,5) = xor(source(i,1),xor(source(1,2),source(1,3)));
     source(i,6) = xor(source(i,2),xor(source(1,3),source(1,4)));
     source(i,7) = xor(source(i,1),xor(source(1,2),source(1,4)));

 end  

%enery per bit to noise spectral density ratio      

EbNo=[-3:1:10];
% 产生白噪声

b=randn(1,N*7/4);

%14种噪声密度

for j = 1:14  

%加入白噪声

    sigma(j) = power(10,(-EbNo(j)/20))/ sqrt (2);
    for i = 1:N*7/4       
        n(i)=sigma(j)*b(i);       
    end
    n = reshape(n,N/4,[]);

    y=source+n;

%接收传输信息  

    for i = 1 : N/4
        for k = 1 : 7
            if y(i,k) > 0
                y(i,k) = 1;
            else
                y(i,k) = 0;
            end
        end
    end 
% 解码，H是奇偶校验矩阵
H = [1 1 1 0 1 0 0
     0 1 1 1 0 1 0
     1 1 0 1 0 0 1
    ];

t_H = H';
syndrome = mod((y* t_H),2);
% 计算误码数
Nberreur(j)=0;
for i = 1 : N/4
    if (syndrome(i,1) == 1) & (syndrome(i,2) == 0) & (syndrome(i,3) == 1)
        Nberreur(j) = Nberreur(j) +1;
        y(i,1) = ~y(i,1);
    end
    if (syndrome(i,1) == 1) & (syndrome(i,2) == 1) & (syndrome(i,3) == 1)
        Nberreur(j) = Nberreur(j) +1;
        y(i,2) = ~y(i,2);
    end
    if (syndrome(i,1) == 1) & (syndrome(i,2) == 1) & (syndrome(i,3) == 0)
        Nberreur(j) = Nberreur(j) +1;
        y(i,3) = ~y(i,3);
    end
    if (syndrome(i,1) == 0) & (syndrome(i,2) == 1) & (syndrome(i,3) == 1)
        Nberreur(j) = Nberreur(j) +1;
        y(i,4) = ~y(i,4);
    end

end

%计算误码率

    Tauxderreur2(j) = Nberreur(j) / N;  

end

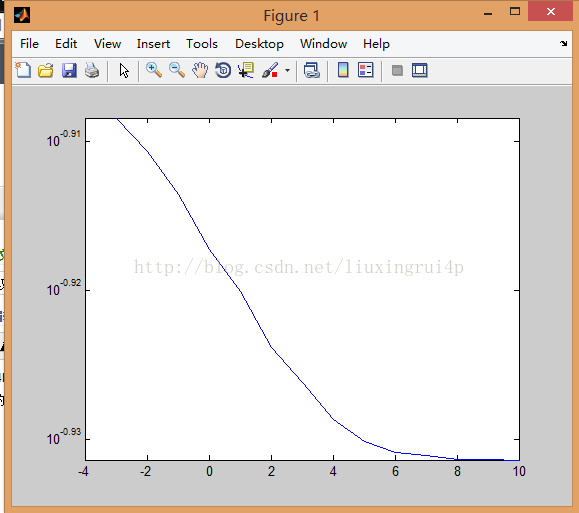
%显示误码率曲线

figure  

semilogy(EbNo,Tauxderreur2);

仿真结果如下：