自动驾驶-使用卡尔曼滤波算法定位和跟踪

参加过科一的人都知道，学车的第一步不是操控车辆而是遵守交规，行车礼让，确保安全。可见安全驾驶才是行车的第一原则。为了确保安全，司机应该观察周围车辆和行人的位置，保持安全距离。自动驾驶的车辆用来感知周围的设备是雷达和激光传感器。本章介绍使用c++实现卡尔曼滤波算法融合雷达和激光传感器完成对物体的感知和追踪，是对udacity自动驾驶课程该项目的学习总结。

以感知行人为例，卡尔曼滤波算法和传感器感知物体的一般流程为：

1. 传感器第一次发现行人，用测量数据对一组描述行人的特征向量初始化得到$x_1$；
2. 进入卡尔曼滤波算法的预测阶段，计算$\Delta t$后的特征向量的预测值$x_t^{\prime }$，方差矩阵$P_t^{\prime }$；预测值的不确定性增加，即$P_t^{\prime }$增加。同时传感器继续测量数据；
3. 进入卡尔曼滤波测量更新阶段， 这时卡尔曼滤波算法得到$\Delta t$时间后的测量值，用这组测量值更新预测值得到估计值$x_t$和$P_t$，更新后的$P_t$降低，即更新后的特征向量更准确。
   
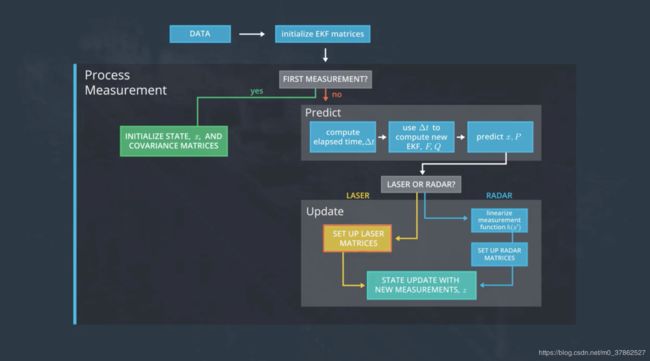
   由上图可见激光和雷达的处理流程不同，激光发送脉冲，在接收反射后的脉冲得到点云，描述周围物体的位置，其优点是空间分辨率高，缺点是容易受天气影响，也不能直接测量目标速度，必须使用两次反射脉冲的位置差计算得出，而且激光传感器体积较大，一般置于车顶。雷达传感器相比于激光传感器分辨率较低，但优点是其采用多普勒效应可以直接算出目标速度，而且受天气影响小，设备体积小安装在车底也能正常工作。

变量定义和初始化

$x$为特征向量，包括水平和垂直方向的位置和速度 $x,y,v_x,v_y$， P为协方差矩阵，表示特征向量的不确定性，由于特征向量之间相互独立，所以P为一个对角矩阵；$F$为状态转换矩阵，完成时刻$t-1$到时刻$t$的状态转换，$H$矩阵将状态向量映射到测量向量的域，Q代表预测值的协方差矩阵, 预测时间越长方差越大，R代表测量值的协方差矩阵。

	  x_ = VectorXd(4);
	  F_ = MatrixXd(4, 4);
      P_ = MatrixXd(4, 4);
      R_laser_ = MatrixXd(2, 2);
      R_rader_ = MatrixXd(3, 3);
      H_laser_ = MatrixXd(2, 4);
      Hj_ = MatrixXd(3, 4);
	  Q_ = MatrixXd(4, 4);
      //measurement covariance matrix - laser
      R_laser_ << 0.0225, 0,
            0, 0.0225;

      //measurement covariance matrix - radar
      R_rader_ << 0.09, 0, 0,
            0, 0.0009, 0,
            0, 0, 0.09;
      
      H_laser_<<1,0,0,0,
            0,1,0,0;

      //state covariance matrix P
      P_ << 1, 0, 0, 0,
      		  0, 1, 0, 0,
       		  0, 0, 1000, 0,
       		  0, 0, 0, 1000;
    
      //the initial transition matrix F_
      F_ << 1, 0, 1, 0,
       		  0, 1, 0, 1,
       		  0, 0, 1, 0,
       		  0, 0, 0, 1;
       		  
	.Q_ <<  dt_4/4*noise_ax, 0, dt_3/2*noise_ax, 0,
			   0, dt_4/4*noise_ay, 0, dt_3/2*noise_ay,
			   dt_3/2*noise_ax, 0, dt_2*noise_ax, 0,
			   0, dt_3/2*noise_ay, 0, dt_2*noise_ay;
  
       previous_timestamp_ = 0;

预测

卡尔曼滤波预测阶段的方程比较简单，代码如下，该函数得到预测后的状态向量$x_t$和协方差$P_t$，预测阶段的协方差矩阵Q可以理解为行人不是匀速行走的，有时快些，有时慢些，所以预测后的状态向量的协方差矩阵增加。

void Predict() {
	x_ = F_ * x_;
	MatrixXd Ft = F_.transpose();
	P_ = F_ * P_ * Ft + Q_ ;
}

测量更新

激光传感器测量更新，K一般称为卡尔曼增益，其会根据预测值的协方差矩阵和测量值的协方差矩阵的大小调整预测值和测量值对估计值的权重，如果预测值的不确定性高，则更新的估计值就更偏向于相信测量值，反之如果传感器性能较差，测量值方差较大，则传感器就更相信预测值。

void KalmanFilter::Update(const VectorXd &z) {
	VectorXd z_pred = H_laser_ * x_;
	VectorXd y = z - z_pred;
	MatrixXd Ht = H_laser_.transpose();
	MatrixXd S = H_laser_ * P_ * Ht + R_laser_;
	MatrixXd Si = S.inverse();
	MatrixXd PHt = P_ * Ht;
	MatrixXd K = PHt * Si;

	//new estimate
	x_ = x_ + (K * y);
	long x_size = x_.size();
	MatrixXd I = MatrixXd::Identity(x_size, x_size);
	P_ = (I - K * H_laser_) * P_;
}

前面介绍了雷达传感器和激光传感器的各自的优缺点，雷达传感器的优点是可以根据多普勒效应直接测出行人的径向速度，雷达传感器得到的是行人相对与车辆移动的相对速度，故雷达传感器测量得到一组极坐标下的数据。

为了比较雷达测量值和预测值的差异，要先把预测值的状态向量转换到极坐标下，转换函数为：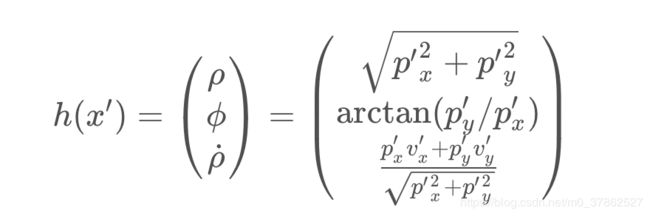

VectorXd Calculate_z_pred() {
    float px = x_[0];
    float py = x_[1];
    float vx = x_[2];
    float vy = x_[3];
    float phi;
    float rho;
    float rhodot;

    rho = sqrt(px*px+py*py);
    phi = atan2(py,px);
    if(rho<0.000001)
        rho = 0.000001;
    rhodot = (px*vx+py*vy)/rho; 
    VectorXd z_pred = VectorXd(3);
    z_pred << rho,phi,rhodot;
    return z_pred;
}

很明显该函数为非线性函数，卡尔曼滤波的理论基础是两个满足高斯分布的函数相乘，得到的结果依然满足高斯分布，但是将预测值转换后得到的是一个非线性函数，这组新的值不再满足高斯分布。

为了使转换后的结果依然满足高斯分布，我们用转换函数$h(x)$的一阶泰勒展开式代替$h(x)$:
$$h(x)\approx h(\mu )+\frac{\partial h(\mu )}{\partial x}(x-\mu )$$
又因为$x$满足均值为0的高斯分布，所以
$$h(x)\approx \frac{\partial h(0)}{\partial x}x$$
由此就已经把非线性方程转换为其变量值为0的偏导数和变量值的乘积组成的线性函数。一个函数的偏导数组成的矩阵可以用雅可比矩阵$H_j$表示：

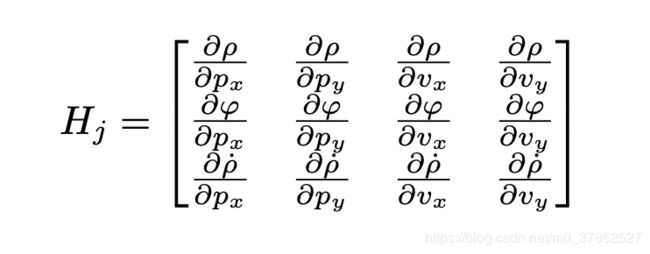
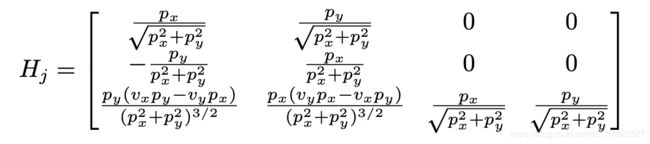
这种解决转移函数非线性化的算法称为扩展卡尔曼滤波算法。
以下为雅可比矩阵的代码实现：

MatrixXd Tools::CalculateJacobian(const VectorXd& x_state) {
	MatrixXd Hj(3,4);
	//recover state parameters
	float px = x_state(0);
	float py = x_state(1);
	float vx = x_state(2);
	float vy = x_state(3);

	//pre-compute a set of terms to avoid repeated calculation
	float c1 = px*px+py*py;
	float c2 = sqrt(c1);
	float c3 = (c1*c2);

	//check division by zero
	if(fabs(c1) < 0.0001){
		cout << "CalculateJacobian () - Error - Division by Zero" << endl;
		return Hj;
	}

	//compute the Jacobian matrix
	Hj << (px/c2), (py/c2), 0, 0,
		  -(py/c1), (px/c1), 0, 0,
		  py*(vx*py - vy*px)/c3, px*(px*vy - py*vx)/c3, px/c2, py/c2;

	return Hj;
}

以下为扩展卡尔曼滤波的测量更新实现，先对预测值进行了极坐标系的转换，然后用雅可比矩阵代替了之前的转移矩阵，确保测量更新后的协方差矩阵$P$依然满足高斯分布，最后就和上边一样根据卡尔曼增益的大小决定预测值和测量值谁对估计值影响更大。

void KalmanFilter::UpdateEKF(const VectorXd &z) {
    VectorXd z_pred = VectorXd(3);
    z_pred  = Calculate_z_pred();
	VectorXd y = z - z_pred;
    while(y(1)>M_PI){
        y(1)-=PI2;
    }
    while(y(1)<-M_PI){
        y(1)+=PI2;
    }
	MatrixXd Ht = Hj_.transpose();
	MatrixXd S = Hj_ * P_ * Ht + R_rader_;
	MatrixXd Si = S.inverse();
	MatrixXd PHt = P_ * Ht;
	MatrixXd K = PHt * Si;

	//new estimate
	x_ = x_ + (K * y);
	long x_size = x_.size();
	MatrixXd I = MatrixXd::Identity(x_size, x_size);
    P_ = (I - K*Hj_)*P_;
}

以上就是本次项目的完整流程，如果学习了前面的卡尔曼滤波原理，对预测和更新的公式就不陌生，本章的难点是理解扩展卡尔曼滤波。由于雷达传感器在极坐标下测值，在更新阶段为了得到预测值和测量值的差值，对预测值使用转移函数将预测值映射到了极坐标下，但是由于转移函数不是线性方程，表征预测值不确定性的协方差矩阵$P$不能直接使用该方程，而必须使用和该方程近似的线性方程，于是根据转移函数的一阶泰勒展开式，用雅可比矩阵对协方差矩阵$P$进行转换，由于是线性转换，所以得到的协方差矩阵依然满足高斯分布。

想要看该项目的完整代码实现戳这里。