运筹优化学习10:分支定界算法求解整数规划问题及其Matlab实现
目录
1 从一个示例入手
2 关于松弛的你要知道的几个概念
3 算法框架
3.1 基本框架
3.2 三种搜索策略
3.3 C++伪代码
4 一个Matlab的实现示例
4.1 linprog函数使用详解
4.2 一个Matlab求解的代码示例解析
5 参考文献
1 从一个示例入手
原始题目:
分支定界的计算过程:
由上述示例可知:
- 在第一次分支时,我们的左侧分支得到的最优解是原问题的一个可行解,终止此分支,将其视为原问题的一个上界;右侧分支得到了-18.5的最优解,但不是原问题的可行解,继续对其进行分支,此时问题的界为【up = -16, lb = -18.5】
- 第二次分支时,左侧分支得到-17.4的可行解,但不是原问题的可行解,继续分支;右侧分支无可行解;此时问题的界更新为【up = -16, lb = -17.4】
- 第三次分支时,左侧分支得到原问题的可行解-17,停止搜索;右侧分支得到了-15.5的最优解,但不是原问题的可行解,且劣于之前确定的界限,停止搜索。
- 得到原问题的最优解为-17
分支定界算法的搜索过程是一个树结构的搜索,每次分支过程都是在解决原始问题的一个子问题。我们将原始的整数线性规划问题松弛为线性规划问题中,得到的线性规划问题的最优解就相当于分支的根节点,其作为所有分支节点的起点进行搜索;在完成一次分支后,如果得到的最优解是原问题的可行解,我们将停止对该分支进行继续搜索;如果不是原问题的可行解,我们会做一次上下界的检查,如果子问题不能产生更好的解,我们将会砍掉该分支;如果位于确定的上下界内,则继续对该分支进行搜索;当所有的分支都不能得到更好的解时,我们就认为得到了问题的最优解,算法即终止。显然,上述过程可以被视为一种目标明确的枚举过程。
2 关于松弛的你要知道的几个概念
松弛模型是为了针对离散优化变量指数级增长而设计的一种辅助性求解方法,其核心在于放松原问题的某些约束或目标函数,使之更易求解,确保对松弛问题的深入分析得到原问题的最优解。
对于整数规划问题,最好的松弛办法为将离散变量松弛为连续变量。
对于优化问题P和R而言,若问题P的可行解都是问题R的可行解,且R的最优解与P的最优解更优或相等,我们便将问题R称为问题P的松弛问题。
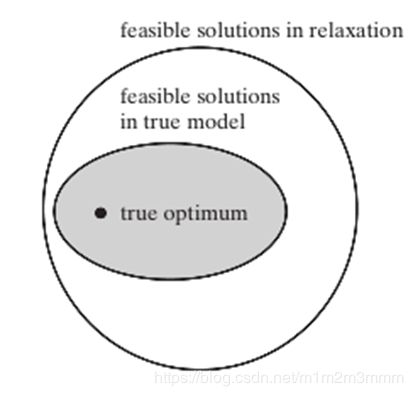
P和R的解空间如下图所示:
- 灰色椭圆为松弛问题最优解所处于的区域
- 黑点为原问题的最优解
- 白色椭圆为问题P的可行解范围
- 最外侧为松弛问题的解空间。
显然,我们可以得出如下结论:
- 松弛问题R的不行解,对于问题P绝对是不可行的;
- 如果松弛问题P的最优解是原问题P的可行解,则其必然是原问题P的最优解;
- 对于最大值模型,松弛问题R的最优解提供了原问题P的上界,且原问题的每一个可行解都可以作为原问题的一个下界;
- 对于最小值问题,松弛问题R的最优解提供了原问题P的下界,且原问题的每个可行解都可以作为原问题的上界;
3 算法框架
有了上面的知识铺垫,我们就可以对分支定界算法的算法进行系统全面的描述了。
3.1 基本框架
| 1. Using a heuristic, find a solution xh to the optimization problem. Store its value, B = f(x_h). (If no heuristic is available, set B to infinity.) B will denote the best solution found so far, and will be used as an upper bound on candidate solutions. 2. Initialize a queue to hold a partial solution with none of the variables of the problem assigned. 3. Loop until the queue is empty: 3.1. Take a node N off the queue. 3.2. If N represents a single candidate solution x and f(x) < B, then x is the best solution so far. Record it and set B ← f(x). 3.3. Else, branch on N to produce new nodes Ni. For each of these: 3.3.1. If bound(N_i) > B, do nothing; since the lower bound on this node is greater than the upper bound of the problem, it will never lead to the optimal solution, and can be discarded. 3.3.2. Else, store Ni on the queue. |
英文看不懂,来个中文的:
再来一个更为直观的流程图:
3.2 三种搜索策略
- 广度优先策略(Breadth-first search,BFS):横向搜索,将同层的节点搜索完毕之后,在进行下一次的搜索;这种搜索可以用FIFO queue实现。首先介绍三种搜索策略:
- 深度优先策略(Depth-first search, DFS):纵向搜索,将一个分支走到底,然后再开下一个分支的搜索;这种搜索可以用LIFO queue也就是栈【后进先出】实现
- 最佳优先搜索(Best-First Search,BFS):基于广度优先策略,先对同层节点使用估价函数对所有节点进行估价,选择估值最小的节点遍历,直至得到最优解位置。可使用优先队列priority queue来实现。
3.3 C++伪代码
// C++实现分支定界算法的伪代码
// 函数功能:我们要求一个最小化问题的最优解
//输入参数:problem 组合优化问题
// objective_function 目标函数值
// lower_bound_function 问题的下界
CombinatorialSolution branch_and_bound_solve(
CombinatorialProblem problem,
ObjectiveFunction objective_function /*f*/,
BoundingFunction lower_bound_function /*g*/)
{
// Step 1 above
double problem_upper_bound = std::numeric_limits::infinity; // = B,设置正无穷无穷对问题的上界进行初始化
CombinatorialSolution heuristic_solution = heuristic_solve(problem); // x_h,启发式算法得到初始解
problem_upper_bound = objective_function(heuristic_solution); // B = f(x_h),将启发式算法得到的解作为问题的上界
CombinatorialSolution current_optimum = heuristic_solution;//设置启发算法的解为当前最优解
// Step 2 above
queue candidate_queue;
// problem-specific queue initialization
candidate_queue = populate_candidates(problem);
while (!candidate_queue.empty()) { // Step 3 above
// Step 3.1
CandidateSolutionTree node = candidate_queue.pop();
// "node" represents N above
if (node.represents_single_candidate()) {
// Step 3.2 如果node是一个候选解,判断其是否小于当前上界,若是则更新上界;否则他就不是最优解,就要停止分支
if (objective_function(node.candidate()) < problem_upper_bound) {
current_optimum = node.candidate();
problem_upper_bound = objective_function(current_optimum);
}
// else, node is a single candidate which is not optimum
}
else {
// Step 3.3: node represents a branch of candidate solutions
// "child_branch" represents N_i above
for (auto&& child_branch : node.candidate_nodes) {
if (lower_bound_function(child_branch) <= problem_upper_bound) {
candidate_queue.enqueue(child_branch); // Step 3.3.2
}
// otherwise, g(N_i) > B so we prune the branch; step 3.3.1
//如果得到一个更差的解,我们就放弃该分支
}
}
}
return current_optimum;
}
4 一个Matlab的实现示例
4.1 linprog函数使用详解
这里调用了Matlab的linprog函数,完整的函数说明文档可在Matlab中输入如下指令:
doc linprog得到如下界面:
可知,该函数可以求解线性规划问题,设计到的参数说明:
| 参数 | 描述 |
| f | 目标函数 |
| A | 系数矩阵 |
| b | 结果列 |
| Aeq | 等式约束系数矩阵;若无等式约束,赋值为[] |
| beq | 等式约束的结果列 |
| lb | 决策变量的下界 |
| ub | 决策变量的上界 |
| x0 | 仅在“active-set”算法中使用到该参数,其余情况下,忽略该参数 |
| options | 优化选项 |
| 返回值 | |
| x | 决策变量的取值 |
| fval | 目标函数的取值 |
| exitflag | 终止标记 |
| output | 包含优化过程信息的结构体 |
| lamda | 当解决方案中包含拉格朗日乘子时,返回的结构体 |
其中的options参数:
exitflag参数:
4.2 一个Matlab求解的代码示例解析
分支定界函数
function [x,val]=kfz(n,f,a,b,aeq,beq,lb,ub)
%获取变量个数的向量
x=zeros(n,1);
% x1=zeros(n,1);
m1=2;
m2=1;
%嗲用lingprog得到线性规划问题的最优解
[x1,val1]=linprog(f,a,b,aeq,beq,lb,ub)
if (x1==0)
x=x1;
val=val1
elseif (round(x1)==x1)%线性问题的最优解都是整数,则它也是原问题的最优解
x=x1;
val=val1
else
e1={0,a,b,aeq,beq,lb,ub,x1,val1};
e(1,1)={e1};
zl=0;
zu=-val1
while (zu~=zl)
for c=1:1:m2
if (m1~=2)
if (cell2mat(e{m1-1,c}(1))==1)
e1={1,[],[],[],[],[],[],[],0};
e(m1,c*2-1)={e1};
e(m1,c*2)={e1};
continue;
end;
end;
x1=cell2mat(e{m1-1,c}(8));
x2=zeros(n,1);
s=0;
s1=1;
s2=1;
lb1=cell2mat(e{m1-1,c}(6));
ub1=cell2mat(e{m1-1,c}(7));
lb2=cell2mat(e{m1-1,c}(6));
ub2=cell2mat(e{m1-1,c}(7));
for d=1:1:n
if (abs((round(x1(d))-x1(d)))>0.0001)&(s==0)
s=1;
lb1(d)=fix(x1(d))+1
if (a*lb1<=b)
s1=0;
end;
ub2(d)=fix(x1(d))
if (a*lb2<=b)
s2=0;
end;
end;
end;
e1={s1,a,b,aeq,beq,lb1,ub1,[],0};
e2={s2,a,b,aeq,beq,lb2,ub2,[],0};
e(m1,c*2-1)={e1};
e(m1,c*2)={e2};
end;
m1=m1+1;
m2=m2*2;
for c=1:1:m2
if (cell2mat(e{m1-1,c}(1))==0)
[x1,val1]=linprog(f,cell2mat(e{m1-1,c}( 2)),cell2mat(e{m1-1,c}(3)),cell2mat(e{m1-1,c}(4)),cell2mat(e{m1-1,c}(5)),cell2mat(e{m1-1,c}(6)),cell2mat(e{m1-1,c}(7)));
e1={cell2mat(e{m1-1,c}(1)),cell2mat(e{m1-1,c}(2)),cell2mat(e{m1-1,c}(3)),cell2mat(e{m1-1,c}(4)),cell2mat(e{m1-1,c}(5)),cell2mat(e{m1-1,c}(6)),cell2mat(e{m1-1,c}(7)),x1,val1};
e(m1-1,c)={e1};
end;
z=val1;
if ((-z)<(-zl))
e1={1,[],[],[],[],[],[],[],0};
e(m1-1,c)={e1};
elseif (abs(round(x1)-x1)<=0.0001)
zl=z
end;
end;
for c=1:1:m2
if (cell2mat(e{m1-1,c}(1))==0)
zu=cell2mat(e{m1-1,c}(9))
end;
end;
for c=1:1:m2
if (-cell2mat(e{m1-1,c}(9))>(-zu))
zu=cell2mat(e{m1-1,c}(9))
end;
end;
end;
for c=1:1:m2
if (cell2mat(e{m1-1,c}(1))==0)&(cell2mat(e{m1-1,c}(9))==zu)
x=cell2mat(e{m1-1,c}(8))
end;
end;
val=-zu;
end;
调用
f = [-1, -5];
A = [-1, 1;
5, 6;];
b = [2; 30];
Aeq = [];
beq = [];
lb = [0; 0];
ub = [4; inf];
[x,val]=kfz(2,f,A,b,Aeq,beq,lb,ub)结果:
| >> Untitled2 x1 = 1.6364
-19.8182
19.8182
2
1 Optimization terminated. zl = -16.0000
-18.6667
-16.0000
-18.6667
2
4
-16.0000 Optimization terminated. zu = -17.4000
3
2 Optimization terminated. zl = -17.0000
-17.0000
-17.0000
-17.0000
-17.0000
-17.0000
2.0000
2.0000
17.0000 >> |
5 参考文献
分支界定法 branch-and-bound 分析与实现
运筹学分支定界法MATLAB