BP神经网络实验报告

BP神经网络实验报告

实验要求

构造一个三层的BP神经网络，完成手写0-9数字的识别

实验步骤

1. 从网上下载MNIST数据集

从官网上得到的数据集有4个，以IDX3-UBYTE的文件类型保存

• train-images.idx3-ubyte 图片训练集，包含6万个数据图片
• train-labels.idx1-ubyte 标签训练集，对应图片训练集的标签
• t10k-images-idx3-ubyte 图片测试集，包含1万个数据图片
• t10k-labels-idx1-ubyte 标签训练集，对应图片测试集的标签
  图片集的文件格式如下
  
  magic number表示数据结构，0x00000803表示类型为unsigned byte，一共有3维。
  标签集的文件格式如下
  
  magic number为0x00000801，表示数据为unsigned byte，表示1维。
  使用python的处理字节模块struct对这个结构进行解析。官网上特别提醒，数据是以大端的形式保存。

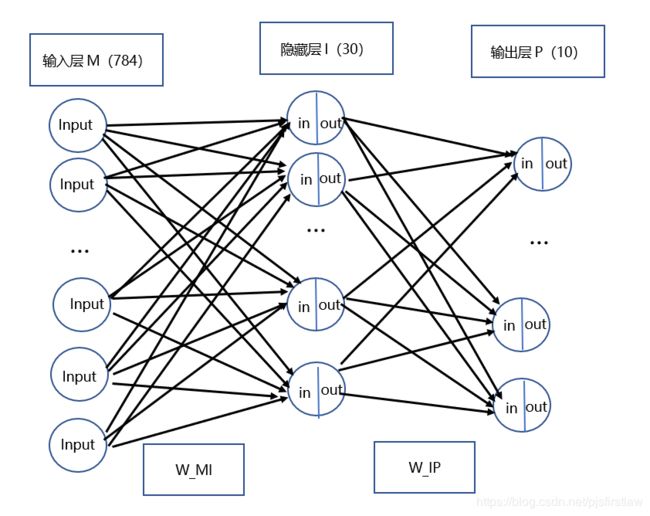
2. 设计神经网络的结构

包含3层，输入层，隐层，输出层。

3. 设计网络的输入和输出

输入层的神经元个数为输入信号的维数（784）。输出层的神经元个数为输出信号的维数，我们采用10维的变量，用10000000000表示结果为0，用010000000000表示结果为1，以此类推。
隐层的个数为30个。这是根据经验公式$\sqrt{m+n}+a,m为输入层个数，n为输出层个数，a\in \{0,1,...10\}$

4. 实现BP网络的错误反传算法，完成神经网络的训练和测试。

BP算法的步骤如下：
第一步：设置变量和参量。初始化输入层与隐层、隐层和输出层之间的权值矩阵V和W，学习速率$\eta$，权值的初始值选为随机的均匀分布$(-2.4/F,2.4/F)$或$(-3/\sqrt{F},3/\sqrt{F})$，F为输入端维数。
第二步：输入一个数据样本，得到隐层输入，使用激励函数激活，得到输出层的输入，再使用激活函数计算输出层的输出。
第三步：使用反向传播算法，计算各层神经元权值矩阵和偏置的梯度。
第四步：更新各层的权值矩阵和偏置。
重置二到四步，直到样本训练完。

5. 算法的具体公式

对输入预处理

输入的向量input是28 * 28的矩阵，矩阵的值范围是0-256。将其变为1 * 784的向量，同时进行预处理操作，使其大小在0-1之间。
$$input[i]=input[i]/256$$

计算隐层输入，输出层输入

$$hidden\_in=input\ast W_{MI}+B_{MI}$$
$$final\_in=hidden\_out\ast W_{IP}+B_{IP}$$

计算隐层输出，输出层输出

使用非线性的激活函数sigmod函数
$$f(x)=\frac{1}{1+e^{-x}}$$
可以计算其导数为（计算梯度时要用到）
$$f^{\prime }(x)=f(x)\ast (1-f(x))$$
因此隐层输出为
$$hiddent\_out=sigmod(hiddent\_in)$$
输出层输出为
$$output=sigmod(final\_in)$$

误差函数

有多种误差函数来衡量学习的好坏，比如交叉熵代价函数和二次代价函数。这里使用后者。单个输入样本的误差为
$$E=\frac{1}{2}(expected-output{)}^2$$

更新输出层权值矩阵和偏置

更新权值矩阵方法是
$$W_{IP}=W_{IP}-\eta \ast \frac{\partial E}{\partial W_{IP}}$$
更新偏置的方法是
$$B_{IP}=B_{IP}-\eta \ast \frac{\partial E}{\partial B_{IP}}$$

下面是计算$\frac{\partial E}{\partial W_{IP}}$的方法

$$\frac{\partial E}{\partial W_{IP}}=\frac{\partial E}{\partial output}\ast \frac{\partial output}{\partial W_{IP}}=\frac{\partial E}{\partial output}\ast \frac{\partial output}{\partial final\_in}\ast \frac{\partial final\_in}{\partial W_{IP}}$$

最右边的乘式的3项很容易求
$$\frac{\partial E}{\partial output}=-(expected-output)$$
$$\frac{\partial output}{\partial final\_in}=f^{\prime }(final\_in)=(1-f(final\_in))\ast f(final\_in)=(1-output)\ast output$$
$$\frac{\partial final\_in}{\partial W_{IP}}=hidden\_out$$
因此
$$\frac{\partial E}{\partial W_{IP}}=-(expected-output)\ast (1-output)\ast output\ast hidden\_out$$

同理可求$\frac{\partial E}{\partial B_{IP}}$

$$\frac{\partial E}{\partial W_{IP}}=\frac{\partial E}{\partial output}\ast \frac{\partial output}{\partial final\_in}\ast \frac{\partial final\_in}{\partial B_{IP}}$$

$$\frac{\partial final\_in}{\partial B_{IP}}=1$$
因此
$$\frac{\partial E}{\partial B_{IP}}=-(expected-output)\ast (1-output)\ast output$$

记梯度grad_p为
$$grad\_p=output\ast (1-output)\ast (expected-output)$$
则
$$\frac{\partial E}{\partial W_{IP}}=grad\_p\ast hiddent\_out$$
$$\frac{\partial E}{\partial B_{IP}}=grad\_p$$

更新隐层权值矩阵和偏置

更新权值矩阵方法是
$$W_{MI}=W_{MI}-\eta \ast \frac{\partial E}{\partial W_{MI}}$$
更新偏置的方法是
$$B_{MI}=B_{MI}-\eta \ast \frac{\partial E}{\partial B_{MI}}$$

下面是计算$\frac{\partial E}{\partial W_{MI}}$的方法

$$\frac{\partial E}{\partial W_{MI}}=\frac{\partial \frac{1}{2}(expected-output{)}^2}{\partial W_{MI}}=\frac{\partial \frac{1}{2}(expected-f(hidden\_in){)}^2}{\partial W_{MI}}=-\sum (expected-output)\ast f^{\prime }(final\_in)\ast \frac{\partial final\_in}{\partial W_{MI}}$$
因为
$$\frac{\partial final\_in}{\partial W_{MI}}=\frac{\partial final\_in}{\partial f(hidden\_out)}\ast \frac{\partial f(hidden\_out)}{\partial hiddent\_out}\ast \frac{\partial hidden\_out}{\partial W_{MI}}$$
所以
$$\frac{\partial E}{\partial W_{MI}}=f^{\prime }(hidden\_in)\ast W_{IP}\ast grad\_p\ast input$$

同理可求$\frac{\partial E}{\partial B_{MI}}$

$$\frac{\partial E}{\partial B_{MI}}=f^{\prime }(hidden\_in)\ast W_{IP}\ast grad\_p$$

记梯度grad_I为
$$grad\_I=f^{\prime }(hidden\_in)\ast W_{IP}\ast grad\_p$$
则
$$\frac{\partial E}{\partial W_{MI}}=grad\_I\ast input$$
$$\frac{\partial E}{\partial B_{MI}}=grad\_I$$

学习速率

上面的$\eta$是学习速率，一般是0.1到0.3。学习速率过快，则权值变化就大，收敛速度快，但容易引起振荡。过小可以避免振荡，但收敛速度慢。

实验结果

在实际的训练中，有两种训练方法，一种是逐个样本输入，每次修改一次权值；另一种是批处理，一次输入多个样本，以平均误差修正权值。而批处理的方法也有2种方法去实现，一种是计数累积的变化，最后再除以一批的数量；另一种是把多个图片作为一个矩阵来输入，这样的好处是计算多张图片只需一次矩阵运算，而前面的累积处理的计算量并没有改变。
以上的方法在实验过程中都有实现，下面对几种方法进行对比。

结果对比

单个处理和累积批处理

在累积批处理中，每10张图修改一次权值和偏置，一共训练6k批次。识别率跟单个输入差不多，有0.91。但当每次处理量变为60，训练1k次时，识别率只有0.7。说明一次的处理量不可以太大。

单个处理和矩阵批处理

用矩阵计算效率大大增加，能进行更多的运算。因此反复将样本进行输入训练。这里当每次处理6张，训练1000k次，最终得到的识别率最好，能达到0.96，原样本的识别率能达到0.98。而且所用的时间是单个处理的两三倍，但训练量时原来的100倍。如果采用累积批处理的话，要实现相同的训练量，则时间要乘以100倍。

学习率与隐藏层个数

下面的数据是从矩阵批处理的方法中的到，每次处理60张，训练100k次。

学习率	隐藏层个数	原样本识别率	测试集识别率	时间
0.05	10	0.9206	0.9186	2min内
0.1	10	0.9324	0.9291	2min内
0.3	10	0.9365	0.9237	2min内
0.5	10	0.9416	0.9333	2min内
1	10	0.9450	0.9259	2min内
0.05	30	0.9372	0.9382	2min内
0.1	30	0.9526	0.9494	2min内
0.3	30	0.9709	0.9600	2min内
0.5	30	0.9723	0.9598	2min内
1	30	0.9812	0.9602	2min内
0.05	100	0.9411	0.9399	3min内
0.1	100	0.9577	0.9565	3min内
0.3	100	0.9818	0.9731	3min内
0.5	100	0.9895	0.9747	3min内
1	100	0.9935	0.9773	3min内

隐层数目越多，训练的时间越长。

批处理数量和批数

下面是在学习率为1，隐藏层为30个时的数据。

一次处理数目	批数	原样本识别率	测试样本识别率	时间
6	10k	0.9395	0.9366	1min内
6	100k	0.9694	0.9583	1min内
60	10k	0.9615	0.9470	1min内
60	100k	0.9804	0.9604	2min内
600	10k	0.9250	0.9237	2min内
600	100k	0.9686	0.9588	18min内