Louvain 算法原理及设计实现
奇技指南
在海量的信息流中,通过精准的算法给用户推荐其感兴趣的内容,已经成为了一个产品吸引用户,获取收益的极其重要的方式。
本篇为算法系列文章,将为大家分享360的算法团队在实践中积累的算法知识及经验,欢迎大家交流分享~
Louvain算法是一种基于多层次优化Modularity的算法,具有快速、准确的优点,在效率和效果上都表现比较好,并且能够发现层次性的社区结构,被认为是性能最好的社区发现算法之一。
模块度
Louvain算法是一种基于图数据的社区发现算法。
原始论文为:
《Fast unfolding of communities in large networks》。
Louvain算法的优化目标为最大化整个数据的模块度,
模块度的计算如下:
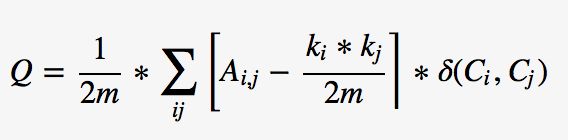
其中m为图中边的总数量,k_i表示所有指向节点i的连边权重之和,k_j同理。A_{i,j} 表示节点i,j之间的连边权重。
有一点要搞清楚,模块度的概念不是Louvain算法发明的,而Louvain算法只是一种优化关系图模块度目标的一种实现而已。
Louvain算法的两步迭代设计
最开始,每个原始节点都看成一个独立的社区,社区内的连边权重为0
步骤1
算法扫描数据中的所有节点,针对每个节点遍历该节点的所有邻居节点,衡量把该节点加入其邻居节点所在的社区所带来的模块度的收益。并选择对应最大收益的邻居节点,加入其所在的社区。这一过程化重复进行指导每一个节点的社区归属都不在发生变化。
步骤2
对步骤1中形成的社区进行折叠,把每个社区折叠成一个单点,分别计算这些新生成的“社区点”之间的连边权重,以及社区内的所有点之间的连边权重之和。用于下一轮的步骤1。
该算法的最大优势就是速度很快,步骤1的每次迭代的时间复杂度为O(N),N为输入数据中的边的数量。步骤2 的时间复杂度为O(M + N), M为本轮迭代中点的个数。
算法实现
数据结构设计
算法数据结构的设计主要有两方面的考虑:
如何高效地存储图中的节点和节点之间的关系
如何在设计的数据结构上高效地扫描数据、进行算法迭代。
当前一些开源的算法实现主要通过hash表或set的结构来存储节点和节点之间的关系。
主要有两个缺点:
维护hash 或 集合结构本身就需要不少内存开销
遍历过程中需要不断地创建、销毁、清空对应的Hash 或 Set 结构,尤其是在遍历不同的节点的邻居节点以及社区这点时。
而且,在遍历过程中,结构对元素的访问也并不是严格O(1)的。
出于以上考虑,我们设计一种更高效的数据结构来存储图中的节点和边,避开使用复杂的数据结构,且在算法迭代过程中不申请多余的空间和空间的销毁操作,具体如下:
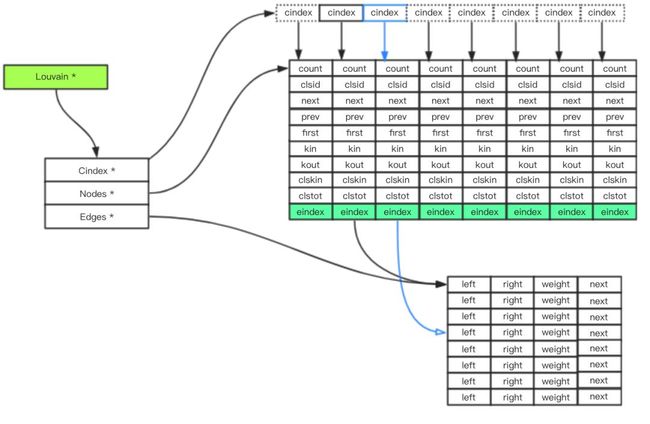
关于节点字段的说明:
count:社区内的节点个数
clsid:节点归属社区的代表节点ID
next:步骤1迭代中下一个属于同一个临时社区的节点
prev:步骤1迭代中上一个属于同一个临时社区的节点
first:属于同一个社区的,除代表节点外的第一个节点,该节点有步骤2 社区折叠的时候生成
kin:稳定社区内部节点之间的互相连接权重之和
kout:稳定社区外部,指向自己社区的权重之和
clskin:临时社区内部节点之间的互相连接权重之和
clstot:稳定社区所有内外部指向自己的连接权重之和
eindex:节点邻居链表的第一个指针,该链表下的所有left,都是本节点自己
关于边数据结构的字段就顾名思义即可。
基于上述结构设计,在给定了一个M个节点,N调边的图所需的空间为:60 * M + 24 * N.
例如:给定1000万给点,2000万边的数据,则需要空间约为:10000000 * 60 + 20000000 * 24 = 1080M.且整个迭代过程中内存环境维持不变。
迭代过程
1、假设我们最开始有5个点,互相之间存在一定的关系(至于什么关系,先不管),如下:

2、假设在进过了步骤1的充分迭代之后发现节点2,应该加入到节点1所在的社区(最开始每个点都是一个社区,而自己就是这个社区的代表),新的社区由节点1代表,如下:
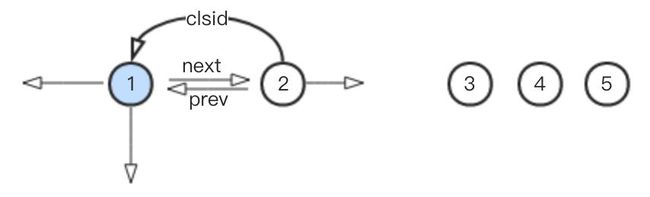
此时节点3,4,5之间以及与节点1,2之间没有任何归属关系。
3、此时应该执行步骤2,将节点1,2组合成的新社区进行折叠,折叠之后的社区看成一个单点,用节点1来代表,如下:

此时数据中共有4个节点(或者说4个社区),其中一个社区包含了两个节点,而社区3,4,5都只包含一个节点,即他们自己。
4、重新执行步骤1,对社区1,3,4,5进行扫描,假设在充分迭代之后节点5,4,3分别先后都加入了节点1所在的社区,如下:
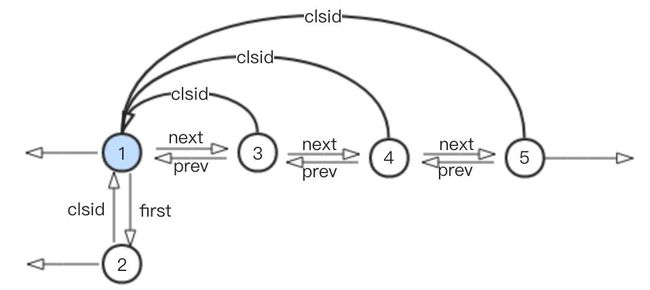
5、进行步骤2,对新生成的社区进行折叠,新折叠而成的社区看成一个单点,由节点1代表,结构如下:
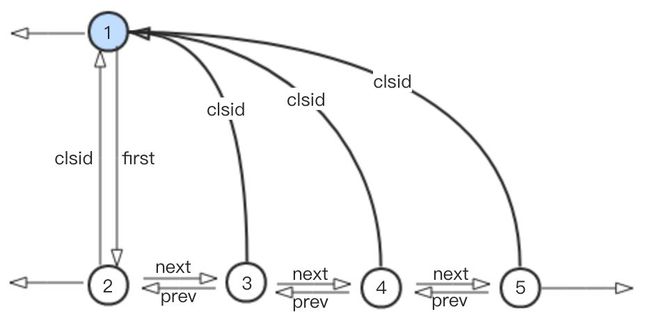
此时由于整个数据中只剩下1个社区,即由节点1代表的社区。
再进行步骤1时不会有任何一个节点的社区归属发生变化,此时也就不需要再执行步骤2,至此, 迭代结束。
代码实现及测试
一个基于上述结构设计的代码实现参见:
https://github.com/liuzhiqiangruc/dml/blob/master/cls/louvain.c
在一个实际的图(70万点,200万边)上进行测试,迭代到完全收敛所需时间为:1.77秒。
实际中往往不需要迭代到每一个点都不发生变化,或者整个图中有多少比例的节点不在发生变化就退出。
本篇为算法系列文章的第3篇,为大家分享了Louvain算法的原理及设计实现。
本文来自360视频信息流算法团队投稿,我们将每周为大家推送一篇算法相关的文章,欢迎大家一起交流学习。
相关推荐
深度残差网络的一波两折
浅谈 梯度下降法/Gradient descent
界世的你当不
只做你的肩膀
无


360官方技术公众号
技术干货|一手资讯|精彩活动
空·
点关注哦~