convex optimization --- affine and convex sets

Convex Optimization

Today, I want to introduce a bit about convex optimization. Convex Optimization is applied in many fields, such as numerical analysis, optimization control, statistical learning and so on.
Next, I will give you some main points of convex optimization.

- Lines and line segment

Now, suppose two points x 1 ≠x 2   in R n   . And all the points of a line passing x 1   and x 2   in R n   can be described as:
y=θx 1 +(1−θ)x 2  
When the parameter θ  equal to 0, y=x 2   and the parameter θ=1  corresponds to y=x 1   . Values of parameter between 0 and 1 correspond to the line segment between x 1   and x 2   .
Here, a figure will show you the basic concept of the lines and line segment.

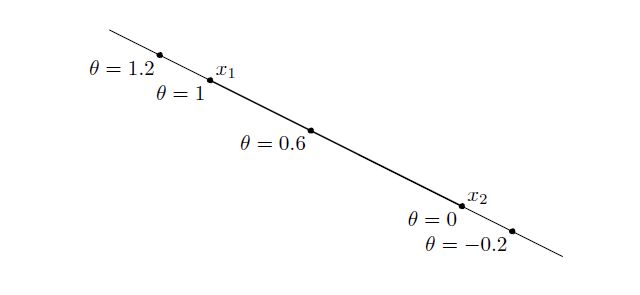
Figure 1 The line passing through x 1   and x 2   is described parametrically by θx 1 +(1−θ)x 2   , where θ  varies over R  . The line segment between x 1   and x 2   , which corresponds to θ  between 0 and 1, is shown darker.

- Affine Set

A set C⊆R n   is affine if the line through any two distinct points in C lies in C, i.e., if for any x 1 ,x 2 ∈C  and θ∈R  , we have θx 1 +(1−θ)x 2 ∈C  . In other words, C contains the liner combination of any points in C.
We can use the mathematics to depict the Affine Set as follow. y=θ 1 x 1 +θ 2 x 2 +...+θ k x k   , where ∑ k i=1 θ i =1  . Using induction from definition of affine set, it can be shown that an affine set contains the affine combination of any points: if C is an affine set, x 1 ,x 2 ,...,x k ∈C,θ 1 +θ 2 +...+θ k =1 
,then the point θ 1 x 1 +θ 2 x 2 +...+θ k x k   also belongs to C.

- Convex Set

A set C is convex if the line segment between any two points in C lies in C, i.e., if for any x 1 ,x 2 ∈C  and any θ  with 0≤θ≤1  , we have θx 1 +(1−θ)x 2 ∈C  .
Here, a figure will show you which set is convex set and which one is nonconvex set.

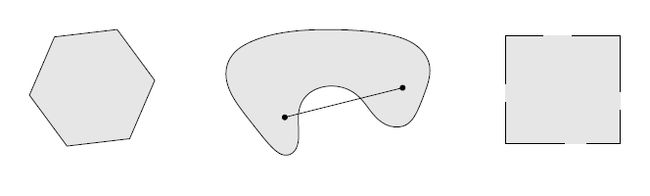
Figure 2 Some simple convex and nonconvex sets. Left. The hexagon, which includes its boundary (shown darker), is convex. Middle. The kidney shaped set is not convex, since the line segment between the two points in the set shown as dots is not contained in the set. Right. The square contains some boundary points but not others, and is not convex.
So a set is convex if every point in the set can be seen by every other point, along an unobstructed straight path between them, where unobstructed means lying in the set. A convex combination of points can be thought of as a mixture or weighted average of the points, with θ i   the fraction of x i   in the mixture.

From this point, we can see convex set is a subset of the affine set. So, if a set is convex, then it must be affine, but the converse is not true.