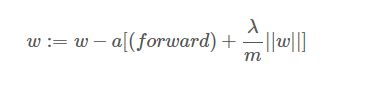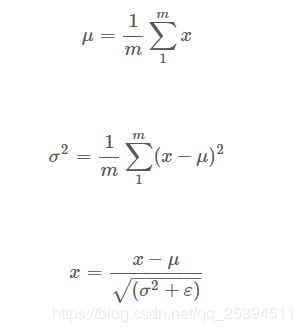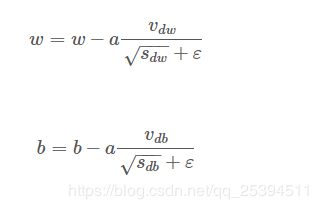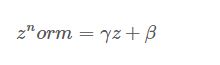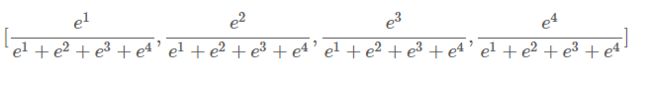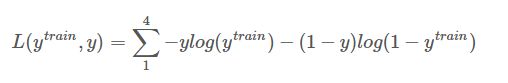神经网络的优化策略

神经网络的优化策略

实用策略

bias/variance

如果训练得到的参数模型对于train集合的拟合效果不好，则为高bias
如果训练得到的参数模型对于test集合的拟合效果不好，则为高variance
我们需要将网络优化到同时具有bias/variance。
在不考虑其他方法的前提下，可以小试一下增加网络层数和迭代次数等这种暴力手段，往往可以有效降低bias但是可能会产生过拟合的情况,产生很高的variance,出现过拟合我们就需要引入其他的方法，如果数据集合本身能够被很好的区分，暴力手段往往是有效的。但是如果数据本身是非结构化的(经常的情况),比如图片分类等，那暴力手段也只是锤在棉花上，因此需要加入一点柔劲,方法叫正则化,这个数学理论本身含义挺广的，我还是觉得英文会更地道点(Regularization),要时刻注意我们的目的是让两个值都能保持在一个较低的水平，例如对于模型A假设训练集准确率为0.99,测试集准确率为0.75，对于模型B训练集准确率为0.90，测试集准确率为0.89那么更能被作为实用的应该是模型B。正则化方法就可以起到这样的作用。

正则化

正则化往往解决的就是过拟合问题，解决过拟合除了正则化还有增加训练数据，这个方法效率会有效，但是成本也高。对于常规神经网络，我们选取的损失函数往往如下：

通常情况下拟合系数参量w已经足够。
上述的正则化方法叫做：L2正则化，还有L1正则化，也就是正则项不平方，这样有人说可以压缩参数量，因为有部分会为0，没有深究，L2用的较多。λ是一个需要人为设定的参数，通常使用交叉验证集合要调试这个参数。添加了正则化项之后我们的前向网络没有变化，反向传播的求导需要改变如下：

从上式可以看出，我们试图让w变得小一点，正则化也成为权重衰减。至于为什么正则化可以放置过拟合，详细的数学推导以后再尝试，现在可以给个直观的解释，假设我们的λλ设置很大，那么最后的w会非常接近0，产生的z=wx+bz=wx+b也很小，中间激活函数往往工作在线性区域比如sigmoid函数，整个网络接近于线性拟合，我们知道网络越简单，越不容易过拟合。因此该参数会有一个合适的值，将网络从过拟合掰回到中间的一个阶段，可以没有那么过拟合，当然网络也不至于过于简单。
另外一种正则化方式是：dropout，该方法的思路很简单，通过某种方法，让某几个节点消失，使网络结构稍微简单化。选取的方法也是有好几种，比如通过随机的[1,0]矩阵去和某层的网络相乘来使节点的权重为0，需要注意的是消除了节点之后，对应的输出值需要除以一个跟节点相关的数，同时损失函数也会跟着改变，具体细节日后再研究。
以上两种用的较多，还有其他几种：一种是数据扩增，比如把训练图片左右翻转，镜像翻转等。另外一种是迭代次数的降低，毫无疑问训练集误差是迭代值的单调递减函数，但是测试值会存在一个最低值，不采取别的算法的话，我们就只能选取这个点，这个方法倒是可以在采取其他算法之后最后采用一下。

归一化输入与梯度消失/爆炸

归一化特征输入就是让输入值的均值和方差处于一个空间零点，通过归一化我们可以使损失函数从一个狭长或者畸形的分布变成一个较圆和均匀的的分布，这种分布可以方便梯度下降能够更快的找到极小值。归一化的公式如下：

梯度消失和爆炸是训练网络非常害怕的东西，这种情况一般出在网络层数比较深的情况，在这种情形下，加入权重矩阵w比1大一点点，我们知道，不同层之间是乘法运算，所以整体是指数级运算，因此w在后面会变得非常大，这很不利于我们训练，同样w比1小一点的话，最后w就会接近0，这样后面的层就影响不到前面的层，同样难以训练。
现在貌似没有很好很好的解决方案（可能是还没开始研读最新论文），以前的老的方案是如何选取一个合适的初始值，通过上面的描述，我们希望特征值越多，我们希望w对应的值越小，因为该层的输出是特征根据w的线性组合再激活，因此我们可以用如下式子：第一层是输入层

λ是一个可以调整的参数，这种方法只能说降低了爆炸或者消失的速度，但是没有解决，留待后面探讨。

优化方法

这里讨论常用的优化反馈环也就是梯度下降的方法

mini-batch

该方法的目的是加快训练速度，将数据集分成数个小块，分别执行梯度下降。不分块的话遍历一次训练集只能进行一次梯度下降，分块的话，就能执行很多次梯度下降。这种方法对于精度来说不一定有好的提升，但是速度是可以加快的。
这种处理方法需要设置的就是分块的大小，如果分块最大，那就是原来的方法，如果分块为1，那就是另外一种方法：随机梯度下降，就是每次随机选取一个数进行梯度下降。
原本的方法除了效率低还是挺好的，mini-batch虽然从算法角度会收敛的慢一点，但是运行起来还是会快一点的，随机梯度下降每次只处理一个数据，会收敛的更慢，而且不能做到完全收敛，会再最优值附近波动。所以选取一个合适batch大小来执行梯度下降会合适的多。

Momentum and RMSProp

Momentum的算法需要用到指数加权平均：直观公式如下：

 

θi是需要的值，vi中间值，因为叠加之后是指数级的平均，所以称之为指数加权平均，该公式表明，越前的数据对后面的数据影响越小，系数的选取影响拟合的程度，系数为1那就是一条平线，系数为0就是全拟合。
Momentum算法就是基于指数加权平均，首先我们明确一点，我们的目的是优化梯度下降，也就是说* 在初始点到全局最优点的直线方向上下降的更快,而在与其垂直的方向上抖动的越缓越好。Momentum算法是做法是，添加了动量v

β一般选取0.9β一般选取0.9上述式子均是赋值操作，该式子的直观解释就是每一步的下降依赖于前一步，速度会越来愈快，但是受限于β<1β<1所以不会无限的加速，但是这种方法对于b是同样的操作，因此抖动理论也会变快，但是权重矩阵对于输出的影响会更大，所以表现出来就是直线方向会加速。
如果我们想要减缓纵轴b的抖动，我们可以用RMSProp方法，该方法添加的是微分项，公式如下：

当dwdw较大的时候我们希望除以一个较大的数来使得w还是很大，因此除以sdw−−−√sdw比较合适，当dbdb较小的时候我们希望除以一个较小的数来使得b还是很小，因此除以sdw−−−√sdw比较合适,
dbdb较大，所以db2db2会较大，所以bb的抖动会变小，dwdw同理，通常情况下dwdw较小，w会减去一个较大的值，所以w会迭代的较快。
通过这种方法可以实现直线方向的加速和垂直方向的减缓。
将Momentum和RMSProp结合就是Adam算法
公式如下：

学习率衰减

加快学习算法的一个办法就是随时间慢慢减少学习率，我们将之称为学习率衰减，假设你要使用 mini-batch 梯度下降法， mini-batch 数量不大，大概 64 或者128个样本，迭代过程会有噪音 ，下降朝向这里的最优值，但是不会精确地收敛，所以你的算法最后在最优值附近摆动，并不会真正收敛，因为我们用的学习率是固定值，但要慢慢减少学习率的话，在初期的时候，学习率还较大，你的学习还是相对较快，但随着变小，你的步伐也会变慢变小，所以最后你的曲线（绿色线）会在最小值附近的一小块区域里摆动，而不是在训练过程中，大幅度在最小值附近摆动。所以慢慢减少的本质在于，在学习初期，你能承受较大的步伐，但当开始收敛的时候，小一些的学习率能让步进小一些。具体操作可以将迭代次数放在分母上，设置一个衰减率参数就可以实现。

超参数与batch归一化

在神经网络中，我们需要学习的权重矩阵或者偏置向量称之为参数，而需要手动设置的比如学习率、衰减率、网络层数、节点数、迭代层数等称之为超参数。业内戏称深度学习工程师就是炼金术士，说的就是工程师在调试超参数的时候，往往就和炼金术一样，东改改细改改，碰运气能不能得到好结果。其实这种说法我是不赞同的，我觉得优秀的工程师才能称之为在炼金，因为他知道改哪些东西会有效果，只是不确定会不会同时影响到别的地方，因为神经网路往往很大，制约因素太多，但是调试的方向和方法包括结果的分析都是有迹可循的。但是拙劣的工程师调试往往就是等同于路边摸奖一样撞大运。所以我们需要摸索摸索参数和网络之间是如何互相影响的。网上的课程推荐还是吴恩达的课，可以对深度学习有直观的认识，想要深入理解，还是得看统计学、概率学、离散数学等书。
言归正传，超参数的调试，业界有几种宏观上的思路，一个是如何选值，一个是如何训练。选值的策略就是如果可选范围比较大，那就采用对数标尺，小的话就线性标尺。训练的话分为国宝模式和鱼子模式，我更喜欢称后一种为土豪模式，第一种就是仔细想好一个参数选择模型，然后训练。另一种就是同时粗略选取多个然后并行训练，毫无疑问后面一种需要你有较多的GPU\TPU。这可能听起来没多大意义，确实也没多大意义，都想得到。
batch归一化是输入归一化的一个扩展，在前面介绍了将输入归一化，可以使得输出均有合适的均值和方差，不过这也只是针对第一层而言，如果将每一层的输出都做归一化，那么下一层的训练也会更加简单，需要提的是，我们归一化的是组合的输出，公式如下：

上面的公式将z归一化横了均值为0，方差为1，在学习中为了使不同的网络有不同的特点，我们需要设定归一化。

这两个也是超参数。batch归一化针对的是某一个batch块做的归一化，所以对整体可能有轻微的正则效果，不过也只是轻微的效果，batch归一化能起作用的直观感受就是，当一个图片的结构发生改变，如何翻转，镜像等，他的均值和方差仍是一定的。所以归一化后的网络变得更加坚实可靠。

softmax回归

这里要提到是一种新的回归方法，以前讨论的都是二类分类器，softmax针对的就是多类分类器比如识别猫、狗、鸡、鸭。这时候我的输出层应该四个，每一个分别对应某一类的概率。这里用的是指数概率，比如[1,2,3,4]对应的输出应该是

对于softmax的训练，需要更改的就是损失函数吧，不再是二类交叉熵，而是多类。

而在计算中会发现，如果某图片属于0类，那么其他类的yy都是0，所以就等于−logytrain−logytrain,注意这是针对单个样本，整体损失就是累加。

总结

这一部分讨论的是神经网络中一些基本或者常用的优化方法和特殊问题的处理策略，其实想要快速上手深度学习直接玩框架就行，但是作为研究者，还是需要懂理论，搞学术更是要继续深研，细推公式，才能在算法上有突破性的优化。框架确实是个好东西，针对大多数人来说，不过更优秀的人，都会在框架的基础上自己定义一些骚操作来满足要求。关于框架的学习笔记，后面多玩几个网络了再整理。