强化学习算法：DQN系列详解

Sarsa

Sarsa 的名称来源于下图所示的序列描述：给定一个状态$S$，个体通过行为策略产生一个行为$A$，即产生一个状态行为对$(S,A)$，环境收到个体的行为后会返回即时奖励$R$以及后续状态$S’$；个体在状态$S’$ 时遵循当前的行为策略产生一个新行为$A’$，个体此时并不执行该行为，而是通过行为价值函数得到后一个状态行为对$(S’,A’)$的价值，利用这个新的价值和即时奖励$R$来更新前一个状态行为对$(S,A)$的价值。与MC算法不同，Sarsa算法在单个状态序列内的每一个时间步，在状态$S$下采取一个行为$A$到达状态$S’$后都要更新状态行为对$(S,A)$的价值$Q(S,A)$。（注意：这里的价值函数Q并不是网络，而是一个表格。）

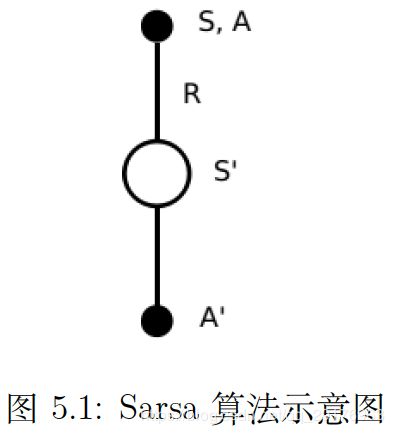
Sarsa算法伪代码为：

Q-Learning

Sarsa是一种on-policy算法，on-policy learning的特点就是产生实际行为的策略与更新价值(评价) 所使用的策略是同一个策略，而off-policy learning 中产生指导自身行为的策略$\mu (a|s)$与评价策略$\pi (a|s)$是不同的策略，具体地说，个体通过策略$\mu (a|s)$生成行为$A$与环境发生实际交互，但是在更新这个状态行为对的价值$Q$时使用的是目标策略$\pi (a|s)$（即$A^{\prime }$由$\pi (a|s)$计算得到）。目标策略$\pi (a|s)$多数是已经具备一定能力的策略，例如人类已有的经验或其他个体学习到的经验。off-policy learning相当于站在目标策略$\pi (a|s)$的“肩膀”上学习。

off-policy learning TD学习任务就是使用TD方法在目标策略$\pi (a|s)$的基础上更新行为价值，进而优化行为策略：

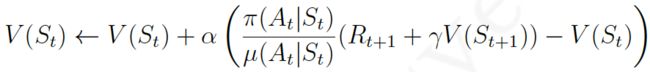
对于上式，我们可以这样理解：个体处在状态$S_t$中，基于行为策略产生了一个行为$A_t$， 执行该行为后进入新的状态$S_{t+1}$，off-policy学习要做的事情就是，比较目标策略和行为策略在状态$S_t$下产生同样的行为$A_t$的概率的比值，如果这个比值接近1，说明两个策略在状态$S_t$下采取的行为$A_t$的概率差不多，此次对于状态$S_t$价值的更新同时得到两个策略的支持。如果这一概率比值很小，则表明目标策略在状态$S_t$下选择$A_t$的机会要小一些，此时为了从目标策略学习，我们认为这一步状态价值的更新不是很符合目标策略，因而在更新时打些折扣。类似的，如果这个概率比值大于1，说明按照目标策略，选择行为$A_t$的几率要大于当前行为策略产生$A_t$的概率，此时应该对该状态的价值更新就可以大胆些。

Q-learning示意图与伪代码如下所示：


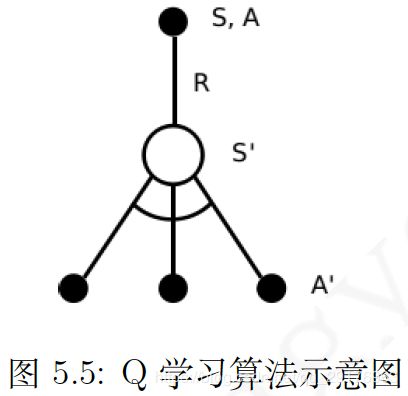
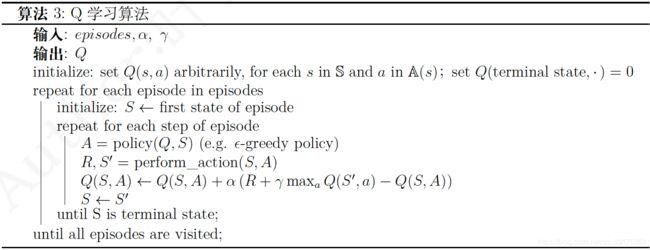
从上图可以看出，虽然Q-learning是一种off-policy算法，但其更新时并没有使用重要性采样。说下个人理解：

• 对于1-step Q-Learning更新公式而言，$(s,a)$可以认为都是给定的（或看成初始），此时$r$已经定了，$(r+\gamma {\max }_{A}Q(s^{\prime },A))$中$s^{\prime }$也已经定了，且这里所求的Q值就是目标策略得到的得到的，因此无需乘IS；
• 对于2-step Q-Learning而言，更新公式变为$(r+\gamma r^{\prime }+{\gamma }^2{\max }_{A}Q(s^{\prime \prime },A))$。同样$(s,a,s^{\prime },r)$给定，此时$r^{\prime },s^{\prime \prime }$是根据执行策略产生的，与目标策略存在偏差，因此需要乘上IS系数；
• 对于1-step off-policy TD而言，更新公式为$(r+V(s^{\prime })-V(s))$，由于$s$到$s^{\prime }$的$a$是由执行策略产生，所以$r$和$s^{\prime }$都是不准确的，因此需要乘上IS。

我们还可以从贝尔曼方程的角度来思考，当前策略下的$Q(s,a)=r+Q(s,a^{\prime })$，其中$r$已知，唯一需要决定的就是$a^{\prime }$，在Q-Learning中$a^{\prime }$就是目标策略产生的(max)；而对于$V(s)=r+V(s^{\prime })$，其中$r,a^{\prime }$都应该是当前策略产生的，但在TD中都是由执行策略产生的。

下面附两张知乎大佬答案里sutton书中的截图加深理解。

DQN

DQN是在Q-learning的基础上做了如下修改：

• 使用深度神经网络来近似状态行为价值函数Q：
  解决了状态空间过大和连续的问题，即“维度灾难”的问题。
• 使用经验回放（Experience Replay）来训练强化学习模型：
  在训练神经网络时，假设训练数据是独立同分布的，但是强化学习数据采集过程中状态之间是具有关联性的，利用这些时序关联的数据训练时，神经网络无法稳定。经验回放打破了数据间的关联性。在强化学习的过程中，智能体将数据保存到一个数据库中，再利用均匀随机采样的方法从数据库中抽取数据，然后利用抽取到的数据训练神经网络。
• 初始化两个Q网络，即使用Target Network：
  原始的Q-learning中，样本标签$Q(S^{\prime },a)$使用的是和训练的$Q(S,A)$相同的网络。这样通常情况下，能够使得$Q(S,A)$大的样本，$R+\gamma Q(S^{\prime },a)$也会大，这样模型震荡和发散可能性变大。而构建一个独立的慢于当前Q-Network的target Q-Network来计算$Q(S^{\prime },a)$，使得训练震荡发散可能性降低，更加稳定。
• Stacked Frames:
  很多游戏里面有些元素的出现是“一闪一闪”的，如果只是传入最新一帧的图片，这样的信息就无法传递给agent，因此，在实际操作的过程中，每个状态都传递了最近四帧的图片给Q-network；从数学的角度上来说，这样的做法让状态的表示更具有马可夫性。
• Frame-skipping:
  在训练的时候每一帧都去判断要采取什么动作相对来讲频率比较高，这会降低agent采样到不同状态的效率，因此，在DQN的工作中会每隔4帧才传递给agent去判断要采取什么动作。

DQN伪代码如下图所示：

在实现DQN代码的时候要特别注意的是，Q网络会输出所有行为的价值，但每次更新的时候我们仅更新behavior Q网络中已选择的$Q(S,A)$的值，其他行为的Q值都置0，无论$Q(S^{\prime },a)$中的$a$是哪一个行为。

Double DQN

DQN无法解决Qlearning的固有缺点——过估计。过估计是指估计的值函数比真实的值函数偏大，如果过估计在所有状态都是均匀的，那么根据贪心策略，依然能够找到值函数最大的动作，但是往往过估计在各个状态不是均匀的，因此过估计会影响到策略决策，从而导致获取的不是最优策略。过估计的产生的原因是在参数更新或值函数迭代过程中采用的max操作导致的。

DQN 中采用 mini-batch SGD 进行梯度更新，如 batch_size=N 表示计算出 N 个 loss 后求和或平均得到一个 loss 再利用 BP 进行网络更新。DQN 的 loss 中每次求得的 target Q 都是取 max 得到的，由于 $E(max(x,y))\ge max(E(x),E(y))$，因此将 N 个 target Q 值先取max操作再求平均，会比先计算 N 个 target Q 值取平均后再 max 要大，即产生了过估计。

DDQN思路并不新鲜，仿照Double Q-learning，一个Q网络用于选择动作，另一个Q网络用于评估动作，交替工作，解决upward-bias问题，效果不错。三个臭皮匠顶个诸葛亮么，就像工作中如果有double-check，犯错的概率就能平方级别下降。

解决方法如下：

• 动作选择：
  下一状态的动作选择由$\mathrm{argmax}{Q}^{\prime }(S^{\prime },a|{\theta }^{\prime })$变为$\mathrm{argmax}Q(S^{\prime },a|\theta )$；
• 动作评估：
  带入上一步得到的行为，$targetQ=R_t+\gamma Q^{\prime }(S_{t+1},\mathrm{argmax}Q(S^{\prime },a|\theta )|{\theta }^{\prime })$；
• 优先回放：
  经验回放时，利用均匀采样并不是高效利用数据的方式，因为智能体经历过的所有数据对于智能体的学习并非具有同等重要的意义。智能体在某个状态的学习效率可能比其余状态要高，优先回放打破了均匀采样，赋予学习效率高的状态更大的采样权重。理想情况下学习效率越高，采样权重应该越大。一个量化定义的方式是，TD偏差$\delta$越大，说明该状态处的值函数与TD目标的差距越大，智能体的更新量越大，因此该处的学习效率越高。我们设样本$i$处的TD偏差为${\delta }_i$ ，则该样本处的采样概率为$P(i)=p_i/{\sum }_k{p}_k$，其中$p_i$由${\delta }_i$决定。通常有两种方式，第一种为$p_i={\delta }_i+ϵ$，第二种为$p_i=1/rank(i)$，$rank(i)$为${\delta }_i$的排序。当我们采用优先回放的概率分布采样时，动作值函数的估计是一个有偏估计，因为采样分布跟动作值函数的分布是两个完全不同的分布，为了矫正这个偏差，我们通常乘以一个重要性采样系数${\omega }_i=(\frac{1}{N}\cdot \frac{1}{p_i}{)}^{\beta }$。当$\beta =1$的时候就可以完全补偿，产生无偏的梯度。做importance ratio另外一个顺带的好处就是，TD误差大的原本会在权值空间上产生更大的步长，这容易导致算法的不稳定；而importance ratio使得这些TD误差大的样本每次对权值的更新步长更小了；这样“小步多次”的更新方式使得算法更加稳定。

DDQN伪代码为：

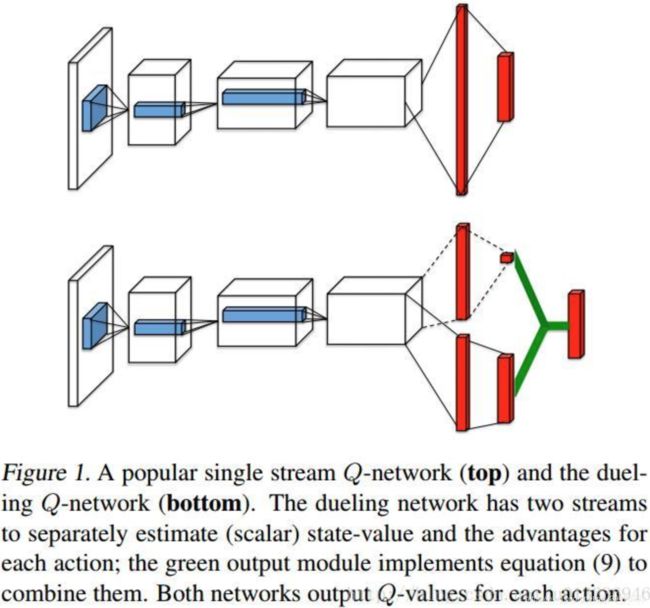
Dueling DQN

在许多基于视觉感知的 DRL 任务中，不同$(s,a)$的值函数是不同的，但是在某些 state下，值函数的大小与动作无关。为处理这种情况，就需要对 DQN 网络结构作一点改变，即将每个$(s,a)$的$Q$值拆分成了两部分： 仅与状态有关的状态价值函数$V$，以及与状态和行为有关的优势函数$A$。即：
$$Q(s,a|\theta ,\alpha ,\beta )=V(s|\theta ,\alpha )+A(s,a|\theta ,\beta )$$
其中$\theta$是卷积层参数，$\alpha ,\beta$分别是两个全连接层支路的参数。而在实际中，一般要将动作优势流设置为单独动作优势函数减去某状态下所有动作优势函数的平均值：
$$Q(s,a|\theta ,\alpha ,\beta )=V(s|\theta ,\alpha )+A(s,a|\theta ,\beta )-\frac{1}{|A|}\sum _{a^{\prime }}A(s,a^{\prime }|\theta ,\beta )$$
这样做可以保证该状态下各动作的优势函数相对排序不变，而且可以缩小$Q$值的范围，去除多余的自由度，提高算法稳定性。

优势函数$A$是$a$对于$s$平均回报的相对好坏，表示选择某个行为额外带来的价值，解决reward-bias问题。RL中真正关心的还是策略的好坏，更关系的是优势，另外在某些情况下，任何策略都不影响回报，显然需要剔除。

Dueling Network网络架构如下。

示例结果如下所示：

上下两行图表示不同时刻，左右两列表示属于$V(s)$和$A(s,a)$。图中红色区域代表$V(s)$和$A(s,a)$所关注的地方。$V(s)$关注于地平线上是否有车辆出现（此时动作的选择影响不大）以及分数；$A(s,a)$则更关心会立即造成碰撞的车辆，此时动作的选择很重要。

References

[1] 叶强, 强化学习入门-从原理到实践.
[2] 知乎：为什么Q-learning不用重要性采样(importance sampling)？
[3] 知乎：深度强化学习（Deep Reinforcement Learning）入门
[4] CSDN：【强化学习】值函数强化学习-DQN、DDQN和Dueling DQN算法公式推导分析
[5] CSDN：深度强化学习——Dueling-DDQN
[6] 知乎：【强化学习入门 2】强化学习策略迭代类方法