神经网络优化方法-梯度下降算法
神经网络优化方法-梯度下降算法
梯度下降算法主要用于优化单个参数的取值, 反向传播算法给出了一个高效的方式在所有参数上使用梯度下降算法。
从而神经网络模型在训练数据的损失函数尽可能小。
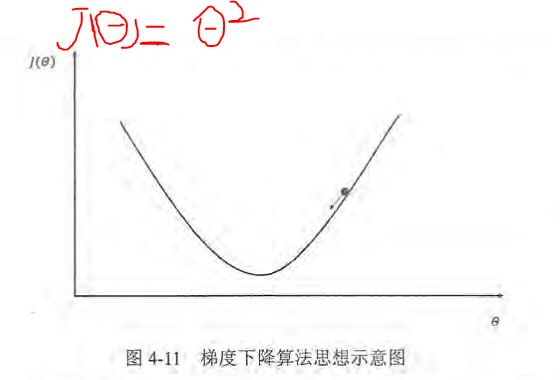
假设损失函数如下:
x轴表示参数取值, y轴表示损失函数的值。, 假设当前的参数和损失函数值的位置为图中小黑点的位置, 那么梯度下降算法将会将参数向x轴左侧移动, 从而使小圆点朝箭头的方向移动。参数的梯度可以通过求偏导的方式计算。
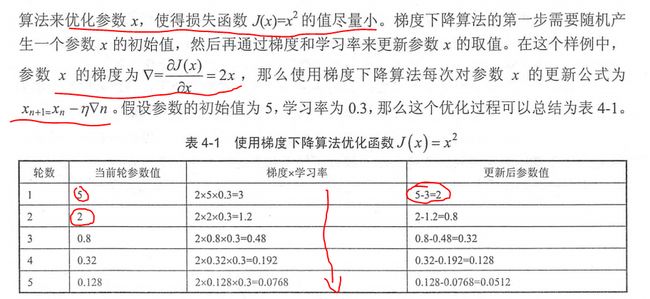
通过以下是实例来解释梯度下降算法作用于损失函数的应用。
神经网络的优化过程与上述样例类似:主要分为两个阶段,第一阶段先通过前向传播算法计算得到预测值,然后将预测值与真实值对比,得出两者之间的差异,第二阶段通过反向传播算法计算损失函数对于每个参数的梯度,再根据梯度和学习率使用梯度下降算法更新每一个参数。
根据例子我们可以看出梯度下降算法可以顺利的使参数值朝着真实的值靠近。但是它并不能保证被优化的函数达到全局最优解。如下图实例所示:
除上述提到的无法达到全局最优的问题外,梯度下降算法的另外一个问题是,由于计算海量数据的损失函数需要的时间过长。
为解决计算时间过长问题引进了随机梯度下降算法(stochastic gradient descent):这个算法优化的不是在全部训练数据上的损失函数, 而是在每一轮迭代中,随机优化某一条训练数据上的损失函数。
但随机梯度下降算法问题也很明显:在某一条数据上损失函数更小不代表在全部数据上损失函数更小。
为了综合梯度下降和随机梯度下降算法的优缺点,我们引入了折中方案:每次计算一小部分训练数据的损失函数,我们称这一小部分数据为一个batch。
因此神经网络的训练大致遵循以下过程:
batch_size = n
x = tf.placeholder(tf.float32,shape=(batch_size,2),name='x-input')
y_ = tf.placeholder(tf.float32,shape=(batch_size,2),name='x-input')
loss = ..
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
with tf.Session as sess:
#参数初始化
...
#迭代更新参数
for i in range(STEPS):
current_X,current_Y = ...
sess.run(train_step,feed_dict={x:current_X,y_:current_Y})