深度学习（正则化的线性回归和逻辑回归）

数据下载地址在这里

Regularized Linear Regression

源码

clear;
clc;
%加载数据
x = load('ex5Linx.dat');
y = load('ex5Liny.dat');
%显示原始数据
plot(x,y,'o','MarkerEdgeColor','b','MarkerFaceColor','r','MarkerSize',10);
%将特征值变成训练样本矩阵
x = [ones(length(x),1),x,x.^2,x.^3,x.^4,x.^5];
[m,n]=size(x);
n=n-1;
%计算参数sidta，并且绘制出拟合曲线
rm=diag([0;ones(n,1)]);%lamda后面的矩阵
lamda=[0 1 10]';
colortype={'g','b','r'};
theta=zeros(n+1,3);
xrange=linspace(min(x(:,2)),max(x(:,2)))';
hold on;
for i = 1:3
    theta(:,i)=inv(x'*x+lamda(i).*rm)*x'*y;%计算参数sida
    norm_sida=norm(theta)
    yrange=[ones(size(xrange)) xrange xrange.^2 xrange.^3,...
        xrange.^4 xrange.^5]*theta(:,i);
    plot(xrange',yrange,strcat(char(colortype(i)),'--'));
    hold on
end
xlabel('x变量');
ylabel('y变量');
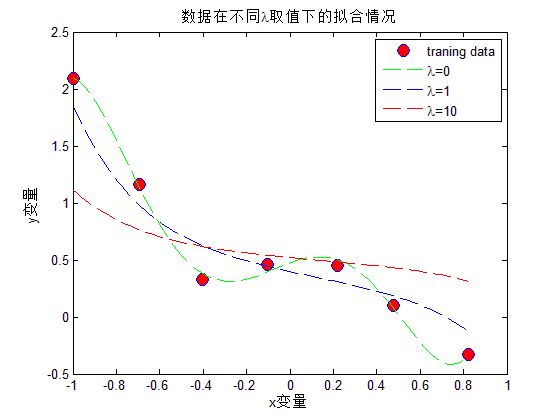
title('数据在不同\lambda取值下的拟合情况');
legend('traning data','\lambda=0','\lambda=1','\lambda=10');
hold off;

实验结果

Regularized Logistic Regression

源码

clear;
clc;
%导入数据
x=load('ex5Logx.dat');
y=load('ex5Logy.dat');
%画出数据分布图
plot(x(find(y==1),1),x(find(y==1),2),'o','MarkerFaceColor','b');
hold on;
plot(x(find(y==0),1),x(find(y==0),2),'r+');
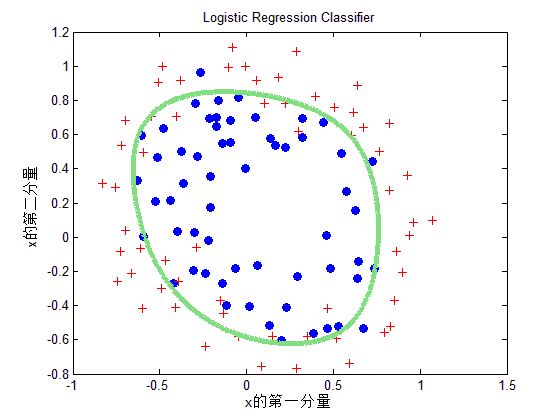
title('Logistic Regression Classifier');
xlabel('x的第一分量');
ylabel('x的第二分量');
x=map_feature(x(:,1),x(:,2));
%%
[m,n]=size(x);
%初始化参数
theta=zeros(n,1);
%内联sigmoid函数
g=inline('1.0 ./ (1.0 + exp(-z))');
%初始化迭代次数
Max_Iter=10;
J=zeros(Max_Iter,1);
%初始化正则化参数
lambda=1;
%训练参数
for i=1:Max_Iter
    %计算损失函数值
    z = x * theta;
    h = g(z);
    J(i)=-1/m*sum(y.*log(h)+(1-y).*log(1-h))...
        +lambda/(2*m)*theta'*theta;
    %计算梯度和Hessian矩阵
     % Calculate gradient and hessian.
    G = (lambda/m).*theta; G(1) = 0; % extra term for gradient
    L = (lambda/m).*eye(n); L(1) = 0;% extra term for Hessian
    grad = ((1/m).*x' * (h-y)) + G;
    H = ((1/m).*x' * diag(h) * diag(1-h) * x) + L;

    % 牛顿法迭代
    theta = theta - H\grad;
end

%画出结果
% Here is the grid range
u = linspace(-1, 1.5, 200);
v = linspace(-1, 1.5, 200);

z = zeros(length(u), length(v));
% Evaluate z = theta*x over the grid
for i = 1:length(u)
    for j = 1:length(v)
        z(i,j) = map_feature(u(i),v(j))*theta;
    end
end
z = z';
% Plot z = 0
% Notice you need to specify the range [0, 0]
contour(u, v, z, [0, 0], 'LineWidth', 4)%在z上画出为0值时的界面，因为为0时刚好概率为0.5，符合要求

实验结果