线性和EWMA指数加权移动平均模型
线性和EWMA指数加权移动平均模型
模型应用场景:
对历史测量值赋权重,对现在t时刻的数值做估计。
1 移动平均
移动平均是是技术分析其中一种分析时间序列数据的工具移动平均可抚平短期波动,将长线趋势或周期显现出来。数学上,移动平均可视为一种卷积。
(1)简单移动平均
简单移动平均(Simple moving average, SMA)是之前n个数值的未作加权算术平均。例如,收市价的10日简单移动平均指之前10日收市价的平均数。设收市价为p1至pn,则方程式为:
(2)加权移动平均
加权移动平均(Weighted moving average, WMA)指计算平均时个别数据乘以不同数值,在技术分析中,n日WMA的最近期一个数值乘以n、次近的乘以n-1,如此类推,一直到0:
其加权为呈递减模型,如下图取n=15,显示第15个数值图形:
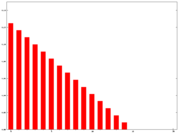
2 线性加权移动平均模型
加权移动平均法不像简单移动平均法那样,在计算平均值时对移动期内的数据同等看待,而是根据愈是近期数据对预测值影响愈大这一特点,不同地对待移动期内的各个数据。对近期数据给予较大的权数,对较远的数据给予较小的权数,这样来弥补简单移动平均法的不足。加权移动平均法常用于进行趋势的预测。
加权平均法的计算公式如下:
式中:
Yn+1 Y n + 1 ——第n+1期加权平均值;
Yi Y i ——第i期实际值;
xi x i ——第i期的权数(权数的和等于1);
n——本期数;
k——移动跨期;
例如我们用该模型应用在高校教师的业绩考核上:
我们就某高校某教室的为样本参考, Yt Y t 表示该教师t时间的业绩数据;一般移动步长去3年,即以前三年的成绩做为综合考虑对象,对其分别加权值;在选取权数的时候,应使离考核期越近的权数越大。权数的选取,听取了一些教育专家的建议,在综合各方面的建议后,将分别a1,a2,a3分别设定为0.5、0.3和0.2。这样,用来计算考核业绩的加权移动平均模型为:
Mt=0.5Yt−1+0.3Yt−2+0.2Yt−3 M t = 0.5 Y t − 1 + 0.3 Y t − 2 + 0.2 Y t − 3
3 EWMA指数加权移动平均
指数移动平均(Exponential Moving Average, EMA或EWMA)是以指数式递减加权的移动平均。各数值的加权而随时间而指数式递减,越近期的数据加权越重,但较旧的数据也给予一定的加权。
加权的程度以常数α决定,α数值介乎0至1。α也可以用N(总数)来代表, a=2N+1 a = 2 N + 1 ,所此处当我们取N=19时,α=0.1。指数加权移动平均后图形应该呈现指数递减形式如下图:

这里假设p=昨日( t0 t 0 )市价,今日( t1 t 1 )EWMA的方程式为:
EMAt1=ap+(1−a)EMAt0 E M A t 1 = a p + ( 1 − a ) E M A t 0
将 EMAt0 E M A t 0 分拆开如下:
EMA=pn(1−a)n+pn−1(1−a)n−1+....+p2(1−a)+p1(1−a)n+(1−a)n−1+....+(1−a)+1 E M A = p n ( 1 − a ) n + p n − 1 ( 1 − a ) n − 1 + . . . . + p 2 ( 1 − a ) + p 1 ( 1 − a ) n + ( 1 − a ) n − 1 + . . . . + ( 1 − a ) + 1
理论上这是一个无穷级数,但由于1-α少于1,各项的数值会越来越细,可以被忽略。
4 总结
很明显指数加权移动平均比线性加权移动平均和简单移动平均都好,考虑了所有过去的参数值,赋予不同的权重估计下一个值。当然这里指数加权,也并不是只会考虑两个变量参数,有时计算移动平均时会加入其他变量,例如,交易量加权会加入交易量的因素等。
csdn数学公式编写可参考:
【1】
https://blog.csdn.net/derrantcm/article/details/51628349#2%E5%A6%82%E4%BD%95%E8%BE%93%E5%85%A5%E4%B8%8A%E4%B8%8B%E6%A0%87
加权移动平均:
【2】
http://wiki.mbalib.com/wiki/%E5%8A%A0%E6%9D%83%E7%A7%BB%E5%8A%A8%E5%B9%B3%E5%9D%87%E6%B3%95
【3】
https://blog.csdn.net/x_i_y_u_e/article/details/44194761