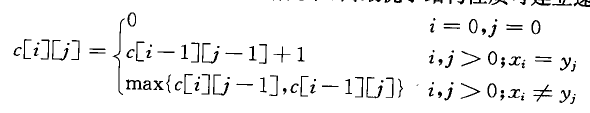最长公共子序列

相关定义

子序列

一个绐定序列的子序列是在该序列中删去若干元素后得到的序列。更加确切的说，若给定序列X=$\{x_1,x_2,...,x_n\}$,则Z=$\{z_1,z_2,...,z_m\}$，X的子序列是指存在一个严格递增下标序列$\{i_1,i_2,...,i_k\}$，使得对于所有$j=1,2,...,k$有$z_j=x_{i_j}$

举例序列$Z=\{B,C.D,B\}$，是序列$X=\{A,B,C,B,D,A,B\}$的子序列，其对应的递增下标序列为$\{2,3,5,7\}$

• 常见误区：子序列必须是连续的元素构成的 ❌

公共子序列和最长公共子序列

公共子序列：给定两个序列X和Y，当另一序列Z既是X的子序列又足Y的子序列时，称Z是序列X和Y的公共子序列。

例如：
$X=\{A,B,C,B,D,A,B\}$ ，$Y=\{B,D,C,A,B,A\}$，序列$\{B,C,A\}$是$X$和$Y$的一个公共子序列，但并不是最长公共子序列。最长公共子序列为$\{B,C,B,A\}$,长度为4，且$X$和$Y$没有长度大于4的公共子序列。

解法

0x01 穷举法

对于X的所有子序列，检查它是否也是为X和Y的公共子序列，并且在检查过程中记录最长的公共子序列。

时间效率分析：X的每个子序列相应于下标集$\{1,2,...,m\}$的一个子集，因此共有$2^m$个不同子序列，因此穷举法需要指数时间

0x02 动态规划

动态规划算法的三个基本要素：
1.最优子结构
2.重叠子问题
3.备忘录方法

1.最优子结构

概念：当问题的最优解包含其子问题的最优解时，称该问题具有最优子结构性质

那么对于最长公共子序列，我们来分析一下它是否具备最优子结构

设序列$X=\{x_1,x_2,...,x_m\}$和$Y=\{y_1,y_2,...,y_n\}$的最长公共子序列为$Z=\{z_1,z_2,...,z_k\}$，则

1. 若$x_m=y_n$，则$z_k=x_m=y_n$，且$Z_{k-1}$是$X_{m-1}$和$Y_{n-1}$的最长公共子序列
   也就是如果两个序列最后一个元素相同，那么它们必定是最长公共子序列的最后一个元素，因此去掉X,Y,Z的最后一个元素之后的$Z_{k-1}$依然是$X_{m-1}$和$Y_{n-1}$的最长公共子序列

2. 若$x_m\ne y_n$，且$z_k\ne x_m$，则$Z$是$X_{m-1}$和$Y$的最长公共子序列
   因为，X的最后一个元素不在Z中，因此去掉它也不影响结果

3. 若$x_m\ne y_n$，且$z_k\ne y_n$，则$Z$是$X$和$Y_{n-1}$的最长公共子序列
   因为，Y的最后一个元素不在Z中，因此去掉它也不影响结果

2.重叠子问题

概念：在用递归算法自顶向下解此问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。

根据在最优子结构部分的讨论，我们发现如果要找出$X=\{x_1,x_2,...,x_m\}$和$Y=\{y_1,y_2,...,y_n\}$的最长公共子序列，我们可以从后往前进行考虑：

1. $x_m=y_n$

当$x_m=y_n$时，$X_m$和$Y_n$的最长公共子序列=$（X_{m-1}$和$Y_{n-1}的最长公共子序列）+x_m(或y_m)$，这里的+指在尾部加上$x_m$

2. $x_m\ne y_n$

这种情况需要求解两个子问题，即找出$X_m$和$Y_{n-1}$的最长公共子序列以及$X_{m-1}$和$Y_n$的最长公共子序列，之后取两者的公共子序列的较长者

因此，根据分析列出表达式

3.伪代码

LCSLength求最长公共子序列长度，LCS求最长公共子序列

LCSLength(X[1..m],Y[1..n])
    //输入：序列X和序列Y
    //输出：序列X和序列Y的最长公共子序列的长度C[m][n]，最长公共子序列构造记录b
    for i←1 to m do
        c[i][0] ← 0
    for i←1 to n do
        c[0][i] ← 0 
    for i←1 to m do
        for j←1 to n do
            if x[i]==y[j] {
                c[i][j] = c[i-1][j-1] + 1
                b[i][j] = 1
            }else if(c[i-1][j] >= c[i][j-1]){
                c[i][j] = c[i-1][j]
                b[i][j] = 2
            }else{
                c[i][j] = c[i][j-1]
                b[i][j] = 3
            }

def LCS(b,x,i,j):
    //输入：数组b,序列X，序列X的长度i，序列Y的长度j
    //输出：序列X和序列Y的最长公共子序列
    if (i==0 or j==0):
        return
    if (b[i][j] == 1):
        LCS(b,x,i-1,j-1)
        print(x[i-1])
    elif (b[i][j] == 2):
        LCS(b,x,i-1,j)
    else:
        LCS(b,x,i,j-1)

4.代码实现

import random
import copy


def random_arr(n):
	tmp = []
	for i in range(n):
		tmp.append(random.choice("ABCDEFG"))
	return ''.join(tmp)

def showTable(c,X,Y):
	m = len(X)
	n = len(Y)
	filed_name = '|   |   '
	row1 = '|   |   '
	for i in range(n):
		filed_name = filed_name + '| {} '.format(Y[i])
		row1 = row1 + '| {} '.format(c[0][i])
	filed_name = filed_name + '|'
	row1 = row1 + '|'
	print(filed_name)
	print(row1)
	for i in range(1,m+1):
		row = '| {} '.format(X[i-1])
		for j in range(0,n+1):
			row = row + '| {} '.format(c[i][j]) 
		row = row + '|'
		print(row)

def LCSLength(X,Y):
	m = len(X)
	n = len(Y)
	c = [[0] * (n+1) for i in range(m+1) ]
	b = copy.deepcopy(c)
	for i in range(1,m+1):
		for j in range(1,n+1):
			if (X[i-1]==Y[j-1]):
				c[i][j] = c[i-1][j-1] + 1
				b[i][j] = 1
			elif (c[i-1][j] >= c[i][j-1]):
				c[i][j] = c[i-1][j]
				b[i][j] = 2
			else:
				c[i][j] = c[i][j-1]
				b[i][j] = 3
	return c,c[m][n],b

def LCS(b,x,i,j):
	if (i==0 or j==0):
		return
	if (b[i][j] == 1):
		LCS(b,x,i-1,j-1)
		print(x[i-1])
	elif (b[i][j] == 2):
		LCS(b,x,i-1,j)
	else:
		LCS(b,x,i,j-1)

if __name__ == '__main__':
	X =(random_arr(random.randint(5,10)))
	Y =(random_arr(random.randint(5,10)))
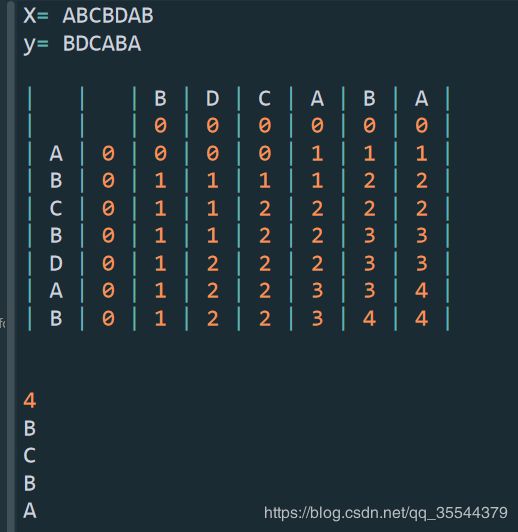
	X = "ABCBDAB"
	Y = "BDCABA"
	print("X= " + X)
	print("y= " + Y+"\n")
	c,length,b = LCSLength(X,Y)
	showTable(c,X,Y)
	print("\n")
	print(length)
	LCS(b,X,len(X),len(Y))