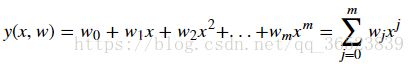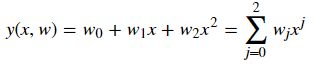多项式回归

多项式回归

多项式回归，回归函数是回归变量多项式的回归。多项式回归模型是线性回归模型的一种，此时回归函数关于回归系数是线性的。由于任一函数都可以用多项式逼近，因此多项式回归有着广泛应用。

直线回归研究的是一个因变量与一个自变量之间的回归问题，但在实际情况中，影响因变量的自变量往往不止一个，例如：羊毛的产量受到绵羊体重、体长、胸围等影响，因此需要进行一个因变量与多个自变量间的回归分析，即多元回归分析。

研究一个因变量与一个或多个自变量间多项式的回归分析方法，称为多项式回归（Polynomial Regression）。如果自变量只有一个时，称为一元多项式回归；如果自变量有多个时，称为多元多项式回归。在一元回归分析中，如果依变量y与自变量x的关系为非线性的，但是又找不到适当的函数曲线来拟合，则可以采用一元多项式回归。

一元m次多项式回归方程为：

二元二次多项式回归方程为：

 

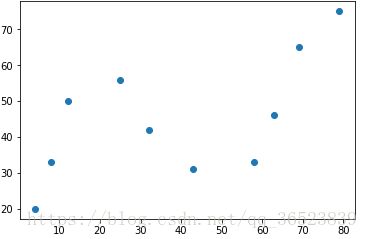
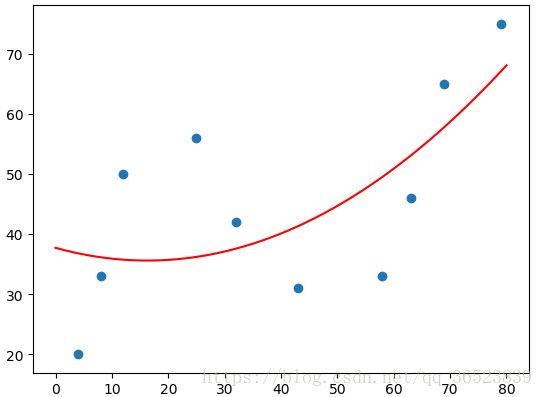
上图的数据，我们可以使用一元2次多项式来拟合，首先，一个标准的一元高阶多项式函数如下：

m 表示多项式的阶数，表示 x 的 j 次幂，w 则代表该多项式的系数。

当我们使用上面的多项式去拟合散点时，需要确定两个要素，分别是：多项式系数 w 以及多项式阶数 m，这也是多项式的两个基本要素。当然也可以手动指定多项式的阶数m的大小，这样就只需要确定系数w的值了。得到以下公式：

如何求解该公式呢？这里使用Scipy的方法。

使用Scipy提供的最小二乘法函数得到最佳拟合参数：

该方法：最小化一组方程的平方和（即可以用来实现最小二乘法） 

import numpy as np
from scipy.optimize import leastsq

# 拟合数据集
x = [4, 8, 12, 25, 32, 43, 58, 63, 69, 79]
y = [20, 33, 50, 56, 42, 31, 33, 46, 65, 75]

def fun(p, x):
    """
    定义想要拟合的函数
    """
    w0,w1 = p  #从参数p获得拟合的参数
    # 如果是二次多项式则：w0,w1,w2 = p ；return w0 + w1*x + w2*x*x  以此类推
    return w0 + w1*x

def err(p, x, y):
    """
    定义误差函数
    """
    return fun(p,x) -y

#定义起始的参数 即从 y = 1*x+1 开始，其实这个值可以随便设，只不过会影响到找到最优解的时间
p0 = [1,1]   #p0 = [1,1,1]    w系数的个数[w0,w1,w2...]

#将list类型转换为 numpy.ndarray 类型，最初我直接使用
#list 类型,结果 leastsq函数报错，后来在别的blog上看到了，原来要将类型转
#换为numpy的类型

x1 = np.array(x)  
y1 = np.array(y)

xishu = leastsq(err, p0, args=(x1,y1))
print(xishu[0])
# xishu[0]，即为获得的参数

一般只要指定前三个参数就可以：

• func 是我们自己定义的一个计算误差的函数，

• x0 是计算的初始参数值

• args 是指定func的其他参数

通过实践后观察，上面实现1次多项式拟合（2次多项式，p0则需要3个值）但其效果都不是很好，所以下面修改代码尝试N(大于2)项拟合

"""
	实现N次多项式拟合
"""
def fit_func(p, x):
	"""根据公式，定义 n 次多项式函数
	"""
	f = np.poly1d(p)   # 这里的np.poly1d函数是用来构造多项式使用的，默认格式为:ax**2+bx+c等，如：ax**3 + bx**2 + cx + d 以此类推
	return f(x)

def err_func(p, x, y):
	"""残差函数（观测值与拟合值之间的差距）
	"""
	ret = fit_func(p, x) - y
	return ret

def n_poly(n):
	"""n 次多项式拟合
	"""
	p_init = np.random.randn(n) # 生成 n 个随机数
	parameters = leastsq(err_func, p_init, args=(np.array(x), np.array(y)))
	return parameters[0]	# 返回多项式系数w0、w1、w2...

k = n_poly(3)	# 与上面的二次多项式结果一致，只是公式顺序不同

"""绘制出 3，4，5，6，7, 8 次多项式的拟合图像
"""
# 绘制拟合图像时需要的临时点
x_temp = np.linspace(0, 80, 10000)
# 绘制子图
fig, axes = plt.subplots(2, 3, figsize=(15,10))

axes[0,0].plot(x_temp, fit_func(n_poly(4), x_temp), 'r')
axes[0,0].scatter(x, y)
axes[0,0].set_title("m = 3")

axes[0,1].plot(x_temp, fit_func(n_poly(5), x_temp), 'r')
axes[0,1].scatter(x, y)
axes[0,1].set_title("m = 4")

axes[0,2].plot(x_temp, fit_func(n_poly(6), x_temp), 'r')
axes[0,2].scatter(x, y)
axes[0,2].set_title("m = 5")

axes[1,0].plot(x_temp, fit_func(n_poly(7), x_temp), 'r')
axes[1,0].scatter(x, y)
axes[1,0].set_title("m = 6")

axes[1,1].plot(x_temp, fit_func(n_poly(8), x_temp), 'r')
axes[1,1].scatter(x, y)
axes[1,1].set_title("m = 7")

axes[1,2].plot(x_temp, fit_func(n_poly(9), x_temp), 'r')
axes[1,2].scatter(x, y)
axes[1,2].set_title("m = 8")
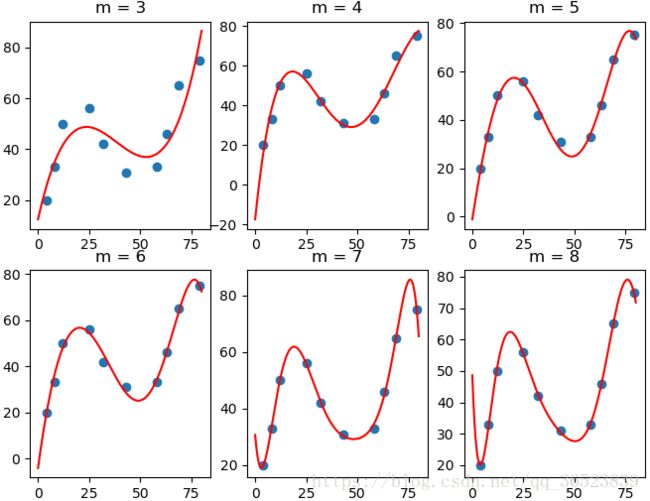
plt.show()

很简单，代码分为两部分，上面为主要的计算系数w的值，下面为直观查看每个次项拟合后的效果图，如下：

可以清楚的看到当3次项（也就是m=3）时，效果还是一般，但从4次项（m=4）后，对于数据的拟合性就明显优于3次项了，当 m=8 时，曲线呈现出明显的震荡，这也就是线性回归实验中所讲到的过拟和（Overfitting）现象，后面再介绍如何解决这个问题。

使用scikit-learn进行多项式拟合：

对于一个二次多项式而言，我们知道它的标准形式为：，但是，多项式回归其实相当于是线性回归的特殊形式（开头也提到）。例如，我们这里令，，那么原方程就转换为：，这也就变成了多元线性回归。完成了一元高次多项式到多元一次项式之间的转换。（如下，看作将多元一次项合并为一个矩阵中线性求解）

举例说明，对于自变量向量  和因变量 ，如果 ：

                      [[ 3]
                 [-2]
                       [ 4]]

则可以通过线性回归模型进行拟合。同样，如果对于一元二次多项式，能得到，构成的特征矩阵，即：

                                        [[ 3.  9.]
                [-2.  4.]
                                         [ 4. 16.]]

那么也就可以使用线性回归进行拟合了。

所以这里有了一个方便的工具，scikit-learn 中，我们可以通过 PolynomialFeatures() 类自动产生多项式特征矩阵

sklearn.preprocessing.PolynomialFeatures(degree=2, interaction_only=False, include_bias=True)

• degree: 多项式次数，默认为 2 次多项式

• interaction_only: 默认为 False，如果为 True 则产生相互影响的特征集。

• include_bias: 默认为 True，包含多项式中的截距项。

通过下面代码解决上面一样的问题：

"""
	使用 PolynomialFeatures 自动生成特征矩阵
"""
from sklearn.preprocessing import PolynomialFeatures

x = np.array(x).reshape(len(x), 1) # 转换为列向量
y = np.array(y).reshape(len(y), 1)

poly_features = PolynomialFeatures(degree=2, include_bias=False)    # 特征矩阵模型构建用来多项式的特征矩阵
poly_x = poly_features.fit_transform(x)    # 通过模型转换x数据

"""
    用线性回归拟合上面转换后的数据
"""
from sklearn.linear_model import LinearRegression

model = LinearRegression()
model.fit(poly_x,y)		# 这里使用转换后的特征矩阵相当于将一元2次转换为二元一次
# print(model.intercept_,model.coef_)

"""绘制拟合图像
"""
x_temp = np.linspace(0, 80, 10000)
x_temp = np.array(x_temp).reshape(len(x_temp),1)
poly_x_temp = poly_features.fit_transform(x_temp)

plt.plot(x_temp, model.predict(poly_x_temp), 'r')
plt.scatter(x, y)
plt.show()         # 得到的结果与上面用leastsq的二次项结果一致

这里二次项的图（degree=2），若设置更高的次项3，4，5（degree=3，4，5），则可以得到上面leastsq方法相同的效果，只需要通过PolynomialFeatures方法生成对应次项的特征矩阵就行。

评价指标

可以使用前一篇文章提到的 平均绝对误差（MAE）、均方误差（MSE）等方法来衡量，具体可以使用sklearn中的以下两个方法：

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error

2次多项式不一定比线性回归的效果好，需要根据具体的测试结果做决定，可以试试更高次的多项式回归预测 ，下面我们便来验证以一下。

make_pipeline通道：

通过实例化 make_pipeline 管道类，实现调用一次 fit 和 predict 方法即可应用于所有预测器。make_pipeline 是使用 sklearn 过程中的技巧创新，其可以将一个处理流程封装起来使用。 更详细的使用可以参考这里

上面的多项式回归中，我们需要先使用 PolynomialFeatures 完成特征矩阵转换，再放入 LinearRegression 中。那么，PolynomialFeatures + LinearRegression 这一个处理流程，就可以通过 make_pipeline 封装起来使用。

以下数据集并非上面的x，y，如下数据（将Year作为特征列train_x，Values为目标值train_y，且数据是按0.7比例分割为训练、测试集）：

"""更高次多项式回归预测
"""
from sklearn.pipeline import make_pipeline

train_x = train_x.reshape(len(train_x),1)
test_x = test_x.reshape(len(test_x),1)
train_y = train_y.reshape(len(train_y),1)

for m in [3, 4, 5]:
    model = make_pipeline(PolynomialFeatures(m, include_bias=False), LinearRegression())
    model.fit(train_x, train_y)
    pre_y = model.predict(test_x)
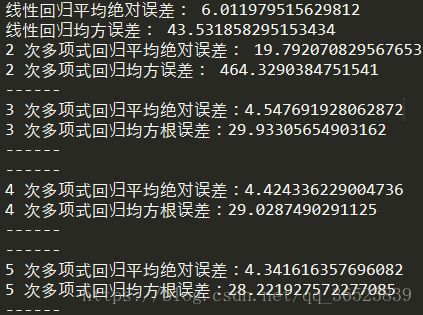
    print("{} 次多项式回归平均绝对误差: ".format(m), mean_absolute_error(test_y, pre_y.flatten()))
    print("{} 次多项式均方根误差: ".format(m), mean_squared_error(test_y, pre_y.flatten()))
    print("---")

可以看到高次项的误差都比线性回归要低，而2次项则要高，所以对于模型均需要进行验证后使用。

好了，上面介绍了 多项式回归的原理与Scipy实现、sklearn构建特征矩阵转为线性运算、Pipeline方便的通道运算、以及误差评判，但还有一个很重要的问题，那就是如何选择最佳的n次项？

几次项才是最佳的选择？

其实这个问题很简单，我们可以设置一个误差指标（MSE、MAE等），然后绘制增加次项后，预测结果的误差值图。观察图形来选择一个合适的次项点（类似肘部法则也可以作为参考）：

"""
	计算 m 次多项式回归预测结果的 MSE 评价指标并绘图
"""
mse = [] # 用于存储各最高次多项式 MSE 值
m = 1 # 初始 m 值
m_max = 10 # 设定最高次数
while m <= m_max:
    model = make_pipeline(PolynomialFeatures(m, include_bias=False), LinearRegression())
    model.fit(train_x, train_y) # 训练模型
    pre_y = model.predict(test_x) # 测试模型
    mse.append(mean_squared_error(test_y, pre_y.flatten())) # 计算 MSE
    m = m + 1

# print("MSE 计算结果: ", mse)
# 绘图
plt.plot([i for i in range(1, m_max + 1)], mse, 'b')
plt.scatter([i for i in range(1, m_max + 1)], mse)

# 绘制图名称等
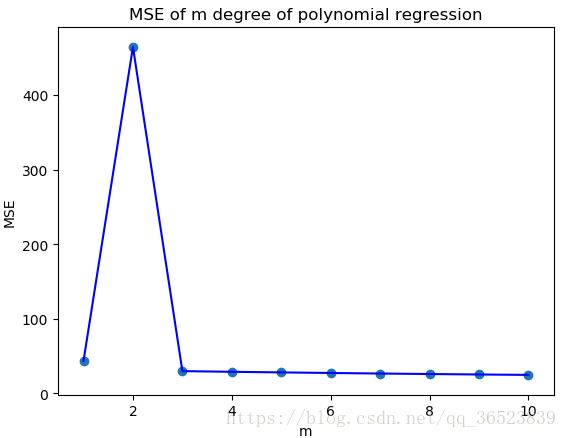
plt.title("MSE of m degree of polynomial regression")
plt.xlabel("m")
plt.ylabel("MSE")
plt.show()

如上图，可以明显看到当次数为3时，误差指标已经趋近于平稳了，所以这里选择3最好，当次数项越多可能会出现过拟合的问题，模型的泛化能力会降低。

 

参考文章：

https://baike.baidu.com/item/%E5%A4%9A%E9%A1%B9%E5%BC%8F%E5%9B%9E%E5%BD%92/21505384?fr=aladdin

https://blog.csdn.net/lanchunhui/article/details/50521648