机械臂模糊PID控制matlab仿真
何为模糊PID:链接
模糊PID理论基础:链接
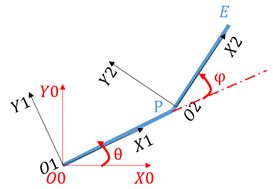
二自由度机械臂运动建模:
末端位置E(x,y),则两个关节角度可以由下式求得:
theta1=atan2(y,x);
% theta1=acos(x/sqrt(x*x+y*y));
c=sqrt(x*x+y*y); % 末端到原点的距离
theta3=acos((c*c+a*a-b*b)/(2*a*c));
theta2=theta1-theta3; % 关节1 角度
phi=pi-acos((a*a+b*b-c*c)/(2*a*b)); %关节2角度
根据上面的建模和模糊PID基础,用模糊PID控制二自由度机械臂,相关代码如下:
%% 主控文件
clc;
clear;
fuzzTab=[-6 -4 -2 0 2 4 6]
% [NB NM NS ZO PS PM PB]
NB=fuzzTab(1);
NM=fuzzTab(2);
NS=fuzzTab(3);
Z0=fuzzTab(4);
PS=fuzzTab(5);
PM=fuzzTab(6);
PB=fuzzTab(7);
% 模糊规则表
PID1.pTab=[NB NB NM NM NS Z0 Z0;
NB NB NM NS NS Z0 Z0;
NB NM NS NS Z0 PS PS;
NM NM NS Z0 PS PM PM;
NM NS Z0 PS PS PM PB;
Z0 Z0 PS PS PM PB PB;
Z0 Z0 PS PM PM PB PB];
PID1.iTab=[NB NB NM NM NS Z0 Z0;
NB NB NM NS NS Z0 Z0;
NB NM NS NS Z0 PS PS;
NM NM NS Z0 PS PM PM;
NM NS Z0 PS PS PM PB;
Z0 Z0 PS PS PM PB PB;
Z0 Z0 PS PM PM PB PB];
PID1.dTab=[PS NS NB NB NB NM PS;
PS NS NB NM NM NS Z0;
Z0 NS NM NM NS NS Z0;
Z0 NS NS NS NS NS Z0;
Z0 Z0 Z0 Z0 Z0 Z0 Z0
PB NS PS PS PS PS PB;
PB PM PM PM PS PS PB];
% 模糊PID控制器 1
PID1.ref=0; % 期望值
PID1.Kp=10; %比例
PID1.Ki=2; %积分
PID1.Kd=4; %微分
PID1.err=0;%偏差
PID1.derr=0;
PID1.max=pi;%最大测量值
PID1.min=-pi;%最小测量值
PID1.maxDltKp=10;%Kp上限
PID1.minDltKp=-5;%Kp下限
PID1.scalKp=0.2;%Kp 权重系数
PID1.maxDltKi=1;%Ki上限
PID1.minDltKi=-2;%Ki下限
PID1.scalKi=0.5;%Ki 权重系数
PID1.maxDltKd=12;%Kd上限
PID1.minDltKd=-4;%Kd下限
PID1.scalKd=0.15;%Kd 权重系数
% 模糊PID控制器 2
PID2=PID1;
PID2.Kp=8; %比例
PID2.Ki=1; %积分
PID2.Kd=2; %微分
PID2.maxDltKp=8;%Kp上限
PID2.minDltKp=-2;%Kp下限
PID2.scalKp=0.9;%Kp 权重系数
PID2.maxDltKi=1;%Ki上限
PID2.minDltKi=-1;%Ki下限
PID2.scalKi=0.5;%Ki 权重系数
PID2.maxDltKd=8;%Kd上限
PID2.minDltKd=-2;%Kd下限
PID2.scalKd=0.15;%Kd 权重系数
%圆心坐标
x0=110;
y0=110;
%半径
R=40;
%连杆长度
a=100;
b=100;
t=1;
% 控制周期
dt=0.05 % 秒
Time=[0]; % 当前时间
aimTheta=[0];% 关节1目标角度
aimPhi=[0];%关节2目标角度
realTheta=[0];% 关节1实际角度
realPhi=[0];%关节2实际角度
errTehta=[0]; % 关节1 角度误差
errPhi=[0]; % 关节2 角度误差
errThetaSum=0;%关节1累积误差
errPhiSum=0;%关节2累积误差
derrTheta=0;%关节1 本次角度误差与上一次角度误差的差值
derrPhi=0;%关节2 本次角度误差与上一次角度误差的差值
% PID 参数(关节1)
% Kp1=10;
% Ki1=2;
% Kd1=4;
% % PID 参数(关节2)
% Kp2=8;
% Ki2=1;
% Kd2=2;
Kp1=8;
Ki1=2;
Kd1=4;
% PID 参数(关节2)
Kp2=6;
Ki2=1;
Kd2=2;
saveW1=[];
saveW2=[];
for i=0:0.1:2*pi+0.1
% theta2=i/150*2*pi;
% phi=i/150*pi;
x=x0+R*cos(i);
y=y0+R*sin(i);
theta1=atan2(y,x);
% theta1=acos(x/sqrt(x*x+y*y));
c=sqrt(x*x+y*y); % 末端到原点的距离
theta3=acos((c*c+a*a-b*b)/(2*a*c));
theta2=theta1-theta3; % 关节1 角度
phi=pi-acos((a*a+b*b-c*c)/(2*a*b)); %关节2角度
aimTheta(end+1)=theta2;
aimPhi(end+1)=phi;
%连杆 P 位置
P=Rot(theta2,'z')*[a;0;0];
% 连杆末端位置(正运动学验证)
E=P+Rot(theta2,'z')*Rot(phi,'z')*[b;0;0];
% PID 偏差
PID1.err=theta2-realTheta(end);
PID2.err=phi-realPhi(end);
deltPID1=Fuzzy2(PID1,realTheta(end),fuzzTab);
deltPID2=Fuzzy2(PID2,realPhi(end),fuzzTab);
PID1.Kp=Kp1+deltPID1(1)*PID1.scalKp;
PID1.Ki=Ki1+deltPID1(2)*PID1.scalKi;
PID1.Kd=Kd1+deltPID1(3)*PID1.scalKd;
PID2.Kp=Kp2+deltPID2(1)*PID2.scalKp;
PID2.Ki=Ki2+deltPID2(2)*PID2.scalKi;
PID2.Kd=Kd2+deltPID2(3)*PID2.scalKd;
PID2.Kp
% PID 控制
w1=PID1.Kp*PID1.err+PID1.derr*PID1.Kd+PID1.Ki*errThetaSum;%关节1 瞬时角速度
w2=PID2.Kp*PID2.err+PID2.derr*PID2.Kd+PID2.Ki*errPhiSum;%关节2 瞬时角速度
realTheta(end+1)=realTheta(end)+w1*dt;
realPhi(end+1)=realPhi(end)+w2*dt;
saveW1=[saveW1,w1];
saveW2=[saveW2,w2];
% 误差
errTehta(end+1)=PID1.err;
errPhi(end+1)=PID2.err;
errThetaSum=errThetaSum+errTehta(end);
errPhiSum=errPhiSum+errPhi(end);
PID1.derr=errTehta(end)-errTehta(end-1);
PID2.derr=errPhi(end)-errPhi(end-1);
% 当前时间
Time(end+1)=Time(end)+dt;
%连杆 P 位置
realP=Rot(realTheta(end),'z')*[a;0;0];
% 连杆末端位置(正运动学验证)
realE=P+Rot(realTheta(end),'z')*Rot(realPhi(end),'z')*[b;0;0];
%末端绘制圆的坐标
rolx(t)=E(1);
roly(t)=E(2);
t=t+1;
subplot(221);
plotrobot(realP(1),realP(2),realE(1),realE(2),rolx,roly); % 绘图验证
axis([-50,200,-50,200]);
hold off
subplot(222);
plot(Time,errTehta,'k',Time,errPhi,'r');
subplot(223);
plot(Time,realTheta,'k',Time,aimTheta,'r');
subplot(224);
plot(Time,realPhi,'k',Time,aimPhi,'r');
pause(0.0000001)
end
%% 模糊PID控制文件
function [deltPID]=Fuzzy2(PID,realAng,fuzzTab)
valErr=LinearQuantization(PID,realAng);% 偏差线性化的值
[indexErr,valueErr]=CalcMemberShip(valErr(1),fuzzTab);%偏差的隶属度计算
[indexDErr,valueDErr]=CalcMemberShip(valErr(2),fuzzTab);%偏差的变化量的隶属度计算
FuzVal(1)=valueErr(1)*(valueDErr(1)*PID.pTab(indexErr(1),indexDErr(1))+valueDErr(2)*PID.pTab(indexErr(1),indexDErr(2)))...
+valueErr(2)*(valueDErr(1)*PID.pTab(indexErr(2),indexDErr(1))+valueDErr(2)*PID.pTab(indexErr(2),indexDErr(2)));
FuzVal(2)=valueErr(1)*(valueDErr(1)*PID.iTab(indexErr(1),indexDErr(1))+valueDErr(2)*PID.iTab(indexErr(1),indexDErr(2)))...
+valueErr(2)*(valueDErr(1)*PID.iTab(indexErr(2),indexDErr(1))+valueDErr(2)*PID.iTab(indexErr(2),indexDErr(2)));
FuzVal(3)=valueErr(1)*(valueDErr(1)*PID.dTab(indexErr(1),indexDErr(1))+valueDErr(2)*PID.dTab(indexErr(1),indexDErr(2)))...
+valueErr(2)*(valueDErr(1)*PID.dTab(indexErr(2),indexDErr(1))+valueDErr(2)*PID.dTab(indexErr(2),indexDErr(2)));
deltPID=LinearDeb(PID,FuzVal);
function retW=LinearQuantization(PID,realAng)
%======= 线性化函数 【-6,6】
% retW(1):偏差的线性化
% retW(1):偏差导数的线性化
error=PID.ref-realAng;
derror=error-PID.err;
retW(1)=6*error/(PID.max-PID.min);
retW(2)=3*derror/(PID.max-PID.min);
function [indexMem,valueMem]=CalcMemberShip(err,fuzzTab)
% 隶属度计算函数
% fuzzTab 模糊规则表
% fuzzTab=[-6 -4 -2 0 2 4 6]
% [NB NM NS ZO PS PM PB]
NB=fuzzTab(1);
NM=fuzzTab(2);
NS=fuzzTab(3);
Z0=fuzzTab(4);
PS=fuzzTab(5);
PM=fuzzTab(6);
PB=fuzzTab(7);
indexMem=[];
valueMem=[];
if err>=NB && err=NM && err=NS && err=Z0 && err=PS && err=PM && err<=PB
indexMem(1)=5;
indexMem(2)=6;
valueMem(1)=-0.5*err+3.0; % y=-0.5x+3
valueMem(2)=0.5*err-2.0; % y=0.5x+1-2
end
indexMem=indexMem+1;
function FuzVal=LinearDeb(PID,FuzVal)
% 限幅处理
if FuzVal(1)>PID.maxDltKp
FuzVal(1)=PID.maxDltKp ;
elseif FuzVal(1)PID.maxDltKi
FuzVal(2)=PID.maxDltKi ;
elseif FuzVal(2)PID.maxDltKd
FuzVal(3)=PID.maxDltKd ;
elseif FuzVal(3) %% 旋转矩阵
function R=Rot(theta,ch)
% @brief: 绕某个轴的旋转矩阵的求法
% @param: theta,绕ch轴旋转的角度;ch,x、y、z中的某个轴
% @ret: 绕 ch 轴的旋转矩阵
% @birth: created by MY on 20200218
c=cos(theta);
s=sin(theta);
switch(ch)
case'x'
R=[1,0,0;0,c,-s;0,s,c];
case'y'
R=[c,0,s;0,1,0;-s,0,c];
case'z'
R=[c,-s,0;s,c,0;0,0,1];
end长期从事机器人学相关研究,涉及机械臂、轮式机器人、四足机器人的建模及仿真,可共同探讨机器人相关问题,可指导课程设计及毕业设计,详询:QQ:2963325158代码链接