美赛数学建模之AHP

25号就是美赛，不掰扯没用的，直接进入正题：

一、定义：层次分析法，英文全称Analytic Hierarchy Process，简称AHP，它是将各种因素层次化，并逐层比较多种关联因素，为分析和预测事物的发展提供可比较的定量依据。AHP特别适用于那些难以完全用定量进行分析的复杂问题，因此在资源分配、选优排序、政策分析、冲突求解以及决策预报等领域得到广泛的应用。

二、主要应用场景
1.评价类、评判类题目，如奥运会的评价、彩票方案的评价、导师和学生的相互选择、建模论文的评价、城市空气质量分析等。

2.资源分配和决策类的题目，如投资资金的分配方案、旅游景点的选择、电脑的挑选、学校的选择、专业的选择等。

3.一些优化问题，尤其是多目标优化问题。

三、AHP步骤
1.建立层次结构模型。以下图为例：

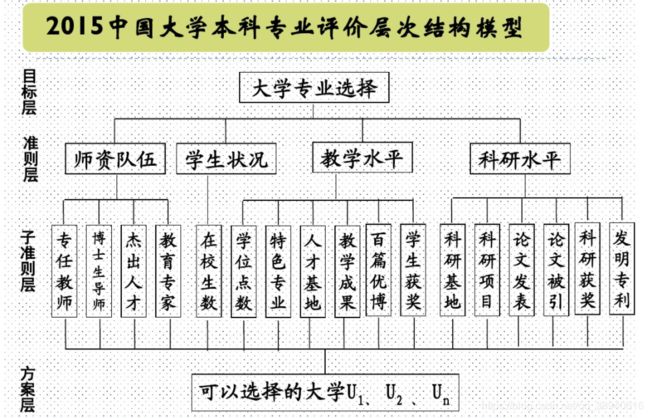
2.构造判断矩阵（成对比较矩阵）
（1）判断比较的标度原则（1~9尺度）

标度	两个元素比较的定义与说明
1	两个具有相同重要性（或相同强）
3	一元素比另一元素稍微重要（或稍微强）
5	一元素比另一元素比较重要（或比较强）
7	一元素比另一元素明显重要（或明显强）
9	一元素比另一元素绝对重要（或绝对强）
2，4，6，8	在上述标准之间折衷时的标度

（2）比较对象与比较次数的关系

对象数量	比较次数
1	0
2	1
3	3
4	6
5	10
6	15
7	21
n	$\frac{n(n-1)}{2}$

（3）矩阵一般形式

（4）矩阵构造规则

• 矩阵对角线元素 a_ii = 1；
• 先填写矩阵右上三角元素。若比较数值在1的左边，则直接填该数值；反之，则填该数值的倒数。

3.层次单排序及一致性检验
对每个成对比较矩阵计算最大特征值及其对应的特征向量，利用一致性指标、随机一致性指标和一致性比例作一致性检验。若检验通过，特征向量（归一化后）即为权向量；若不通过，需要重新构造成对比较矩阵。

4.层次总排序及一次性检验
计算最下层对最上层总排序的权向量。利用总排序一致性比例

$$CR=\frac{a_{1}C{I}_1+a_{2}C{I}_2+\cdots +a_{m}C{I}_m}{a_{1}R{I}_1+a_{2}R{I}_2+\cdots +a_{m}R{I}_m}$$
$$CR<0.1$$

进行检验。若通过，则可按照总排序权向量表示的结果进行决策，否则需要重新考虑模型或重新构造那些一致性比例CR较大的成对比较矩阵。

四、AHP求解权重矩阵及一次性检验实现方法（基于MATLAB R2014a）

% % AHP权重计算
% % 数据读入
clc
clear all
A = [1 2 6; 1/2 1 4; 1/6 1/4 1]; % 判断矩阵
% % 一致性检验和权向量运算
[n,n] = size(A);                 % 获取指标个数
[v,d] = eig(A);                  % 求取判断矩阵的特征值v和特征向量d
r = d(1,1);                     
CI = (r - n)/(n - 1);            % 计算一致性检验指标CI（越接近0越好）
% % RI为平均随机一致性指标取值表(1-15阶)
RI = [0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.52 1.54 1.56 1.58 1.59];
CR = CI / RI(n);                 % 计算一致性比例CR
if CR < 0.10
    CR_Result = '通过';
else
    CR_Result = '不通过，需要重新构造判断矩阵';
end

% % 权向量计算
w = v(:,1) / sum(v(:,1));
w = w';

% % 结果输出
disp('该判断矩阵权向量计算报告：');
disp(['一致性指标：',num2str(CI)]);
disp(['一致性比例：',num2str(CR)]);
disp(['一致性检验结果：',num2str(CR_Result)]);
disp(['特征值：',num2str(r)]);
disp(['权向量：',num2str(w)]);

通常情况下仅需将判断矩阵输入到程序中，其他地方都不需要修改，直接运行就可以得到对应结果。

五、AHP建模实例
1.旅游问题
（1）建模

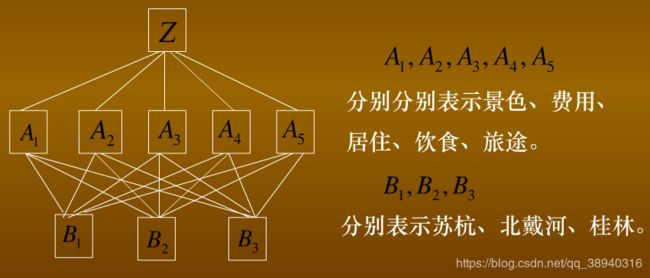
（2）构造判断矩阵（成对比较矩阵）
先是Z-A的判断矩阵，设为A：
$$A=\left[\begin{array}{ccccc}1& \frac{1}{2}& 4& 3& 3\\ 2& 1& 7& 5& 5\\ \frac{1}{4}& \frac{1}{7}& 1& \frac{1}{2}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{5}& 2& 1& 1\\ \frac{1}{3}& \frac{1}{5}& 3& 1& 1\end{array}\right]$$
接着是A-B的判断矩阵（$A_1，\cdots ，A_5$各1个），设为$B_1，\cdots ，B_5$：

$B_1=\left[\begin{array}{ccc}1& 2& 5\\ \frac{1}{2}& 1& 2\\ \frac{1}{5}& \frac{1}{2}& 1\end{array}\right]$ $B_2=\left[\begin{array}{ccc}1& \frac{1}{3}& \frac{1}{8}\\ 3& 1& \frac{1}{3}\\ 8& 3& 1\end{array}\right]$ $B_3=\left[\begin{array}{ccc}1& 1& 3\\ 1& 1& 3\\ \frac{1}{3}& \frac{1}{3}& 1\end{array}\right]$

$B_4=\left[\begin{array}{ccc}1& 3& 4\\ \frac{1}{3}& 1& 1\\ \frac{1}{4}& 1& 1\end{array}\right]$ $B_5=\left[\begin{array}{ccc}1& 1& \frac{1}{4}\\ 1& 1& \frac{1}{4}\\ 4& 4& 1\end{array}\right]$

（3）计算层次单排序的权向量和一致性检验
将六个判断矩阵分别传入MATLAB程序中，得到如下结果：

判断矩阵	一致性检验指标CI	一致性比例CR	一致性检验结果	特征值	权向量
$A$	0.018021	0.01609	通过	5.0721	（0.2636，0.47584 ，0.053815，0.098068， 0.10868）
$B_1$	0.0027676	0.0047716	通过	3.0055	（0.59538，0.27635 ，0.12827）
$B_2$	0.00077081	0.001329	通过	3.0015	（0.081935，0.23634 ，0.68172）
$B_3$	-1.1102e-15（实取0）	-1.9142e-15 （实取0）	通过	3	（0.42857，0.42857 ，0.14286）
$B_4$	0.0046014	0.0079334	通过	3.0092	（0.63371，0.19192 ，0.17437）
$B_5$	-4.4409e-16（实取0）	-7.6567e-16 （实取0）	通过	3	（0.16667，0.16667 ，0.66667）

（4）计算层次总排序权值和一致性校验
由上表可以看出，A的特征值${\lambda }_{max}=5.0721$ ,相应的特征向量为：$$W^{(2)}=(0.2636，0.47584，0.053815，0.098068，0.10868{)}^T$$
每一行的元素分别代表景色、费用、居住、饮食、旅途准则的权重。
而各准则对应的特征向量矩阵如下：
$$W^{(3)}=\left[\begin{array}{ccccc}0.59538& 0.081935& 0.42857& 0.63371& 0.16667\\ 0.27635& 0.23634& 0.42857& 0.19192& 0.16667\\ 0.12827& 0.68172& 0.14286& 0.17437& 0.66667\end{array}\right]$$
这个矩阵的每一行则分别代表苏杭、北戴河、桂林在五个准则方面的权重大小。
故$$W=W^{(3)}{W}^{(2)}=\left[\begin{array}{c}0.2993\\ 0.2453\\ 0.4554\end{array}\right]$$
而$$CR=\frac{a_{1}C{I}_1+a_{2}C{I}_2+\cdots +a_{m}C{I}_m}{a_{1}R{I}_1+a_{2}R{I}_2+\cdots +a_{m}R{I}_m}=0.0027<0.1$$
故层次总排序通过一致性校验。
$W$中，各方案权重排序为$B_3>B_1>B_2$，故最后的决策为$B_3$，即去桂林。

六、AHP的优点和局限性
1.系统性：AHP把研究对象作为一个系统，按照分解、比较判断、综合的思维方式进行决策，成为继机理分析、统计分析之后发展起来的系统分析的重要工具。

2.实用性：AHP把定性和定量方法结合起来，能处理许多用传统的最优化技术无法着手的实际问题，应用范围很广，同时，这种方法使得决策者与决策分析者能够相互沟通，决策者甚至可以直接应用它，这就增加了决策的有效性。

3.简洁性：具有中等文化程度的人即可以了解AHP的基本原理并掌握该法的基本步骤，计算也非常简便，并且所得结果简单明确，容易被决策者了解和掌握。

4.只能从原有的方案中优选出一个出来，没有办法得出更好的新方案。

5.该法中的比较、判断以及结果的计算过程都是粗糙的，不适用于精度较高的问题。

6.从建立AHP模型到给出成对比较矩阵，人主观因素对整个过程的影响很大，这就使得结果难以让所有的决策者都接受。当然采取专家群体判断的办法是克服这个缺点的一种途径。