matlab元胞自动机入门详解

元胞自动机的初步理解

• 对元胞自动机的初步认识
  元胞自动机（CA）是一种用来仿真局部规则和局部联系的方法。典型的元
  胞自动机是定义在网格上的，每一个点上的网格代表一个元胞与一种有限的状
  态。变化规则适用于每一个元胞并且同时进行。
• 元胞的变化规则&元胞状态
  典型的变化规则，决定于元胞的状态，以及其（ 4 或 8 ）邻居的状态。
• 元胞自动机的应用
  元胞自动机已被应用于物理模拟，生物模拟等领域。
• 元胞自动机的matlab编程
  结合以上，我们可以理解元胞自动机仿真需要理解三点。一是元胞，在matlab中可以理解为矩阵中的一点或多点组成的方形块，一般我们用矩阵中的一点代表一个元胞。二是变化规则，元胞的变化规则决定元胞下一刻的状态。三是元胞的状态，元胞的状态是自定义的，通常是对立的状态，比如生物的存活状态或死亡状态，红灯或绿灯，该点有障碍物或者没有障碍物等等。

更新画面

动态的展示变化过程，需要掌握下面三条语句

h = imagesc(你的元胞矩阵)
在按照一定规则更行状态的循环中，
set(h,'cdata',你的更新后的元胞矩阵)
drawnow或者pause(时间间隔)

元胞自动机的有趣实例

生命游戏机

生命游戏是英国数学家约翰·何顿·康威在1970年发明的细胞自动机。它包括一个二维矩形世界，这个世界中的每个方格居住着一个活着的或死了的细胞。一个细胞在下一个时刻生死取决于相邻八个方格中活着的或死了的细胞的数量。通常情况，游戏的规则就是：当一个方格周围有2或3个活细胞时，方格中的活细胞在下一个时刻继续存活；即使这个时刻方格中没有活细胞，在下一个时刻也会“诞生”活细胞。
听说许多程序猿都喜欢玩这个
规则是：
¾ 对周围的 8 个近邻的元胞状态求和
¾ 如果总和为 2 的话，则下一时刻的状态不改变
¾ 如果总和为 3 ，则下一时刻的状态为 1
¾ 否则状态= 0
元胞的邻居定义通常有以下三种范式，这里采用第二种，认为其周围八个点为邻居。

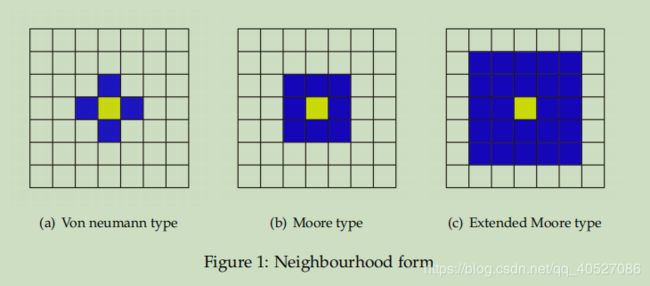
简单仿真效果：

全部代码如下

%% 设置GUI按键
plotbutton=uicontrol('style','pushbutton','string','运行', 'fontsize',12, 'position',[150,400,50,20], 'callback', 'run=1;');
erasebutton=uicontrol('style','pushbutton','string','停止','fontsize',12,'position',[250,400,50,20],'callback','freeze=1;');
quitbutton=uicontrol('style','pushbutton','string','退出','fontsize',12,'position',[350,400,50,20],'callback','stop=1;close;');
number = uicontrol('style','text','string','1','fontsize',12, 'position',[20,400,50,20]);
%% 元胞自动机设置
n=200;
%初始化各元胞状态
z = zeros(n,n);
sum = z;
cells = (rand(n,n))<.6;
% 建立图像句柄
imh = image(cat(3,cells,z,z));
set(imh, 'erasemode', 'none')
% 元胞更新的行列数设置
x = 2:n-1;
y = 2:n-1;
% 主事件循环
stop= 0; run = 0;freeze = 0; 
while stop==0
    if run==1
        % 计算邻居存活的总数
        sum(x,y) = cells(x,y-1) + cells(x,y+1) + cells(x-1, y) + cells(x+1,y)...
            + cells(x-1,y-1) + cells(x-1,y+1) + cells(x+1,y-1) + cells(x+1,y+1);
        % 按照规则更新
        cells = (sum==3) | (sum==2 & cells);
        set(imh, 'cdata', cat(3,cells,z,z) )
        stepnumber = 1 + str2double(get(number,'string'));
        set(number,'string',num2str(stepnumber))
    end
    if freeze==1
        run = 0;
        freeze = 0;
    end
    drawnow
end

扩散

规则，先把中间点置为1，每一时间步对每一点，如果周围
八个点和为偶数，则变为0，为奇数则变为 1

效果：

代码：

% 颜色控制
Map = [1 1 1; 0 0 0];
colormap(Map);
% 设置网格大小
S = 121;
L = zeros(S);
% 把中间一个数设置为 1 作为元胞种子
M = (S+1)/2;
L(M, M) = 1;
Temp = L;
imagesc(L);
% 计算层数
Layer = (S-1)/2 + 1;

for t=2:Layer
    for x=M-t+1:M+t-1
       if x==M-t+1 || x==M+t-1

          for y=M-t+1:M+t-1
            SUM = 0;
            for m=-1:1
               for n=-1:1
                  if x+m>0 && x+m<=S && y+n>0 && y+n<=S
                     SUM = SUM + L(x+m, y+n); 
                  end
               end
            end
            SUM = SUM - L(x, y);
            Temp(x, y) = mod(SUM, 2);
          end
          
       else
            y = M-t+1;
            SUM = 0;
            for m=-1:1
               for n=-1:1
                  if x+m>0 && x+m<=S && y+n>0 && y+n<=S
                     SUM = SUM + L(x+m, y+n); 
                  end
               end
            end
            SUM = SUM - L(x, y);
            Temp(x, y) = mod(SUM, 2);
            
            y = M+t-1;
            SUM = 0;
            for m=-1:1
               for n=-1:1
                  if x+m>0 && x+m<=S && y+n>0 && y+n<=S
                     SUM = SUM + L(x+m, y+n); 
                  end
               end
            end
            SUM = SUM - L(x, y);
            Temp(x, y) = mod(SUM, 2);
       end
    end
    L = Temp;
    imagesc(L);
    % 速度控制
    pause(0.2);
end

双车道交通流仿真

这个稍微难一点

脚本

% 车流密度不变下的双向两车道仿真（T 字形路口）
% v:平均速度，d:换道次数（1000 次）p:车流密度
nl = 80 ;% 车道长度（偶数）
nc = 2; % nc:双向车道数目
dt= 0.01; % 仿真步长时间
fp = 20; % 车道入口处新进入车辆的概率（列向量）
nt=10000;% 仿真步长数目
chance=0.5;
chance1=0.5;
[ v, d, p ] = multi_driveway_with_crossroad_exit ( nl,nc,dt,fp,nt,chance,chance1);
 

规则&状态转移函数

function [ v, d, p ] = multi_driveway_with_crossroad_exit( nl,...
    nc,dt,fp,nt,chance,chance1)
% fp:车道入口处新进入车辆的概率向量（2,3,5 车道）——输入参数
% chance:交叉口处车辆行为的概率向量(5 车道右转,3车道右转）——输入参数
 %构造元胞矩阵
 B=ones(nc+1+nl/2,nl+3);
 %不可行车道
 B(nc/2+1,[1:nl/2 nl/2+4:nl+3])=1.2;   
 B(nc+2:nc+1+nl/2,[1:nl/2 nl/2+4:nl+3])=1.2;
 %初始化仿真元胞状态（1 为无车，0 为有车）
 bb1=B([1:nc/2 nc/2+2:nc+1],:);bb2=B(:,nl/2+3);bb3=B(:,nl/2+1);
 bb1(bb1~=0)=1;
 bb2(bb2~=0)=1;
 bb3(bb3~=0)=1;
 B([1:nc/2 nc/2+2:nc+1],:)=bb1;B(:,nl/2+3)=bb2;B(:,nl/2+1)=...
     bb3;B(1:nc+1,nl/2+1:nl/2+3)=1;
 B(1:nc/2,end)=0;B(nc/2+2:nc+1,1)=0;B(end,nl/2+3)=0;
 %显示初始交通流图
 figure();
 H=imshow(B,[]);
 set(gcf,'position',[241 132 560 420]) ;%241 132 560 420
 set(gcf,'doublebuffer','on'); %241
 title('cellular-automation to traffic modeling','color','b');
 %初始化化存储元胞上车辆状态的矩阵
 S(1:nc*2+2,nl/2-2) = 0;
 Q(1:nc*2+2,1:2) = 0;
 C=zeros(nc+1,3);
 %初始化换道频率、平均速度、车流密度相关变量
 ad = 0;
 av(1:nt) = 0;
 ap(1:nt) = 0;
 s = 1;flag= 0;flag1=0;%flag、flag1 用于标示小区出口的车是否为左转车辆
 flag2=0;
 for n = 1:nt
%六个路段的长度。
A=[
B(1:nc/2,nl/2 :-1:1);
B(nc/2+2:nc+1,1:nl/2);
B(1:nc/2,nl+3:-1:nl/2+4);
B(nc/2+2:nc+1,nl/2+4:nl+3);
B(nc+1+nl/2:-1:nc+2,nl/2+3)';
B(nc+2:1:nc+1+nl/2,nl/2+1)'
];
c=B(1:nc+1,nl/2+1:nl/2+3);
 %确定前 n-2 个车辆的状态
 S(:,:) = 0;
 S(A(:,1:end-2)==0&A(:,2:end-1)==1&A(:,3:end)==1)=2;%快速行驶的车
 S(A(:,1:end-2)==0&A(:,2:end-1)==0)=3;%停车的车
 S(A(:,1:end-2)==0&A(:,2:end-1)==1&A(:,3:end)==0)=1;%慢速行驶的车
 %确定最后两个元胞的状态
 Q(:,:)= 0;
 Q(A(:,end-1)==0&A(:,end)==0) = 3;
 Q(A(:,end-1)==0&A(:,end)==1) = 1;
 if c(3,1)==0
     if randnl/2)
 av(s) = V/N;
 s = s+1;
 end
 %在车道入口处随机引入新的车辆
 A([2;3;5],1)=(round(fp.*rand(3,1))&A([2;3;5],1));
 A(A~=0)=1;
 if flag2==1
     A(6,1)=0;
     flag2=0;
 end
 %将新的车辆加入元胞矩阵中
 B(1,1:nl/2)=A(1:nc/2,end:-1:1);
 B(3,1:nl/2)=A(nc/2+1:nc,:);
 B(1,nl/2+4:nl+3)=A(nc+1:nc*3/2,end:-1:1);
 B(3,nl/2+4:nl+3)=A(nc*3/2+1:2*nc,:);
 B(nc+2:nc+1+nl/2,nl/2+3)=A(2*nc+1,end:-1:1)';
 B(nc+2:nc+1+nl/2,nl/2+1)=A(3*nc,:)';
 B(1:3,nl/2+1:nl/2+3)=c(:,:);
 %显示交通流图
 set(H,'CData',B);
%计算这个时间段每个时间点的指标（速度与车流量）。
 d = ad;
 p = mean(ap);
 v = sum(av)/s;
 disp([v,p])
%仿真步长
 pause(dt);
 end
end