关于MATLAB实现的数字信号处理(二)
上一篇:关于MATLAB实现的数字信号处理(一)
下一篇:关于MATLAB实现的数字信号处理(三)
文章目录
- 上一篇:关于MATLAB实现的数字信号处理(一)
- 下一篇:关于MATLAB实现的数字信号处理(三)
- 离散时间傅里叶变换的性质
- 1.离散时间傅里叶变换的卷积性质
- 2.离散时间傅里叶变换的时间反转性质
- 3.离散傅里叶变换和离散傅里叶逆变换的计算
离散时间傅里叶变换的性质
1.离散时间傅里叶变换的卷积性质
e − j w 0 n g [ n ] ⟶ D T F T G ( e j ( w − w 0 ) ) e^{-j w_{0} n} g[n] \stackrel{\mathrm{DTFT}}{\longrightarrow} G\left(e^{j\left(w-w_{0}\right)}\right) e−jw0ng[n]⟶DTFTG(ej(w−w0))
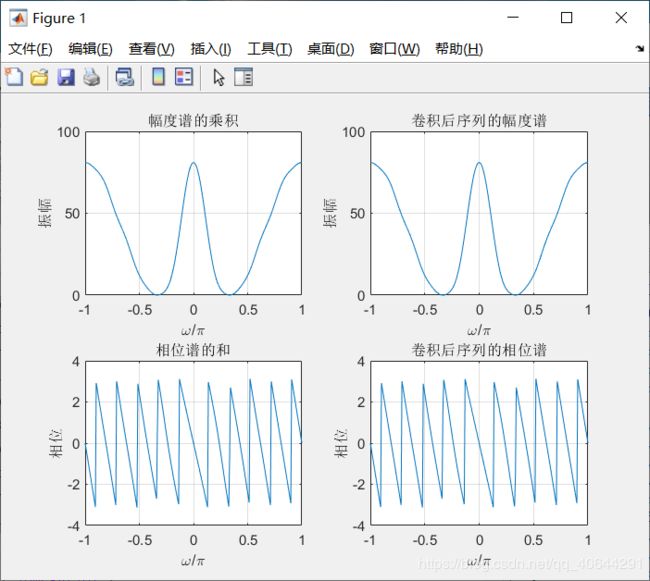
调用卷积函数conv()和先对两个序列做离散时间傅里叶变换,再做乘积相比较
实现代码
% DTFT的卷积
clf;
w = -pi:2*pi/255:pi;
x1 = [1 3 5 7 9 11 13 15 17];
x2 = [1 -2 3 -2 1];
y = conv(x1,x2);%卷积
h1 = freqz(x1, 1, w);%求h1的离散傅里叶变换
h2 = freqz(x2, 1, w);%求h2的离散傅里叶变换
hp = h1.*h2;%h1与h2相乘
h3 = freqz(y,1,w);%求卷积的离散傅里叶变换
%画出幅度谱的乘积
subplot(2,2,1)
plot(w/pi,abs(hp));grid
title('幅度谱的乘积')
%画出卷积后序列的幅度谱
subplot(2,2,2)
plot(w/pi,abs(h3));grid
title('卷积后序列的幅度谱')
%画出相位谱的和
subplot(2,2,3)
plot(w/pi,angle(hp));grid
title('相位谱的和')
%画出卷积后序列的相位谱
subplot(2,2,4)
plot(w/pi,angle(h3));grid
title('卷积后序列的相位谱')
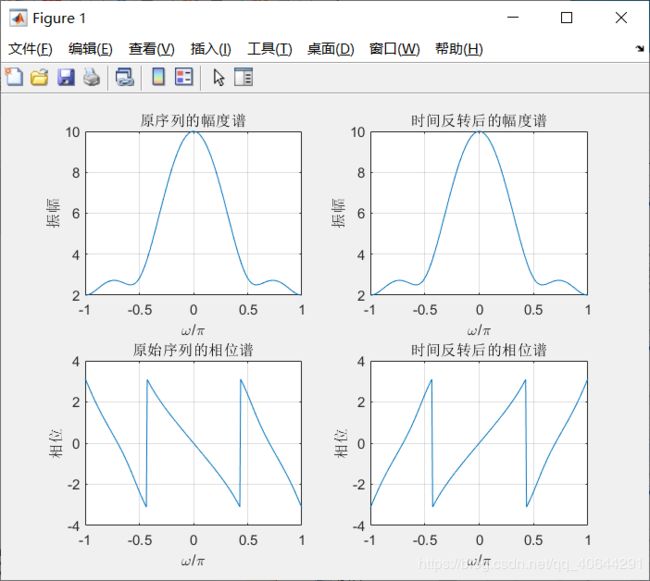
2.离散时间傅里叶变换的时间反转性质
g [ − n ] ⟶ D T F T G ( e − j w ) g[-n] \stackrel{\mathrm{DTFT}}{\longrightarrow} G\left(e^{-j w}\right) g[−n]⟶DTFTG(e−jw)
实现代码
% 离散傅里叶变换的时间反转性质
clf;
w = -pi:2*pi/255:pi;
num = [1 2 3 4];%系统函数的分子多项式的系数
L = length(num)-1;%分母多项式系数矩阵的长度
h1 = freqz(num, 1, w);%求h1的离散时间傅里叶变换
h2 = freqz(fliplr(num), 1, w);%求对h1进行反转后的离散时间傅里叶变换
h3 = exp(w*L*i).*h2;%对h2进行频移
%画出原序列的幅度谱
subplot(2,2,1)
plot(w/pi,abs(h1));grid
xlabel('\omega/\pi');
ylabel('振幅');
title('原序列的幅度谱')
%画出时间反转后的幅度谱
subplot(2,2,2)
plot(w/pi,abs(h2));grid
xlabel('\omega/\pi');
ylabel('振幅');
title('时间反转后的幅度谱')
%画出原始序列的相位谱
subplot(2,2,3)
plot(w/pi,angle(h1));grid
xlabel('\omega/\pi');
ylabel('相位');
title('原始序列的相位谱')
%画出时间反转后的相位谱
subplot(2,2,4)
plot(w/pi,angle(h3));grid
xlabel('\omega/\pi');
ylabel('相位');
title('时间反转后的相位谱')
3.离散傅里叶变换和离散傅里叶逆变换的计算
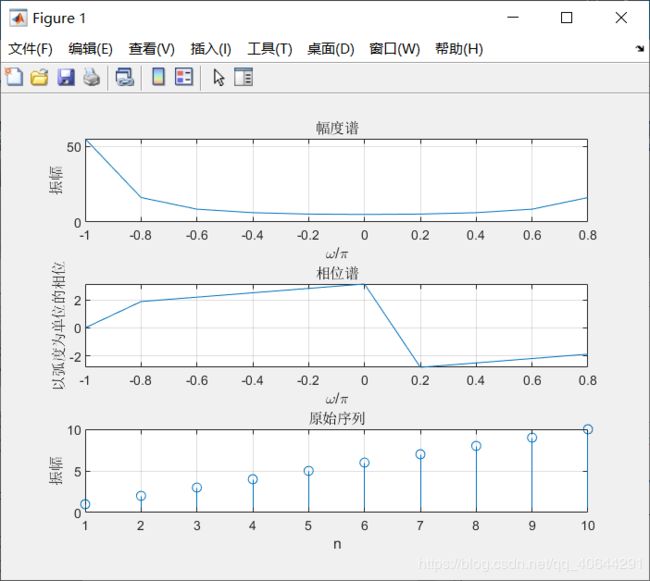
1.写一个MATLAB程序,计算并画出长度为N的L点离散博里叶变换X[k]的值,其中L>=N,然后计算并画出L点离散傅里叶逆变换X[k]。对不同长度N和不同的离散傅里叶变换长度L,运行程序。
%DFT
%原始序列是x=[1 2 3...],
%其长度由N决定
clf;
N=10;L=20;
% w1代表频率点
wl=-pi:2*pi/L:pi;
n=1:L;
for i=1:L
w(i)=wl(i);
end
for i=1:N
x(i)=i;
end
xx=[x zeros(1,L-N)];
y=fft(xx,L);
xk=ifft(y,L);
subplot(3,1,1)
plot(w/pi,abs(y));
grid
xlabel('\omega/\pi');
ylabel('振幅');
title('幅度谱');
subplot(3,1,2)
plot(w/pi,angle(y));
grid
xlabel('\omega/\pi');
ylabel('以弧度为单位的相位');
title('相位谱');
subplot(3,1,3)
stem(n,xk);grid
xlabel('n');
ylabel('振幅');
title('原始序列')
实验结果
N=10 L=20

N=10 L=10
2.用一个N点复数离散傅里叶变换计算两个长度为N的实数序列的N点离散傅里叶变换,并将结果同直接使用两个N点离散傅里叶变换得到的结果进行比较。
若g[n]和h[n]表示两个长度为N的实序列,G[k]和H[k]分别表示它们各自的N点离散傅里叶变换。定义x[n]= g[n]+ji[n],那么x[n]为长度为N的复数序列,它的N点离散傅里叶变换X[k],我们可以通过下式有效地计算G[k]和H[k]:
G [ k ] = 1 2 ( X [ k ] + X ∗ [ ( − k ) N ] ) H [ k ] = 1 2 j ( X [ k ] − X ∗ [ ( − k ) N ] ) \begin{aligned} G[k] &=\frac{1}{2}\left(X[k]+X^{*}\left[(-k)_{N}\right]\right) \\ H[k] &=\frac{1}{2 j}\left(X[k]-X^{*}\left[(-k)_{N}\right]\right) \end{aligned} G[k]H[k]=21(X[k]+X∗[(−k)N])=2j1(X[k]−X∗[(−k)N])
实现代码
%用一个N点复数离散傅里叶变换
%计算两个长度为N的实数序列的N点离散傅里叶变换,
%并将结果同直接使用两个N点离散傅里叶变换得到的结果进行比较。
clf;
g=[1 2 3 4 5 6 7 8 9 10];
h=[11 12 13 14 15 16 17 18 19 20];
N1=20;N2=10;
% w1代表频率点1
% w2代表频率点2
w1=-pi:2*pi/(N1-1):pi;
w2=-pi:2*pi/(N2-1):pi;
x=g+1i*h; %表示出x[n]
x1=g-1i*h; %表示出x[n]的共轭
xk=fft(x,N2); %计算x[n]的离散傅里叶变换
x1k=fft(x1,N2);%计算x[n]共轭的离散傅里叶变换
%根据公式有效地计算g[n]和h[n]的离散傅里叶变换
gk=1/2*(xk+x1k);
hk=1/(2*1i)*(xk-x1k);
%根据fft函数分别计算g[n]和h[n]的离散傅里叶变换
gk1=fft(g,N2);
hk1=fft(h,N2);
%画出G[k]的幅频响应
subplot(4,2,1)
stem(abs(gk));
axis([0,10,0,70]);
grid
xlabel('\omega/\pi');
ylabel('振幅');
title('G[k]的幅度谱')
%画出G[k]的相频响应
subplot(4,2,2)
stem(angle(gk));
axis([0,10,-4,4]);
grid
xlabel('\omega/\pi');
ylabel('以弧度为单位的相位');
title('G[k]相位谱')
%画出H[k]的幅频响应
subplot(4,2,3)
stem(abs(hk));
axis([0,10,0,200]);
grid
xlabel('\omega/\pi');
ylabel('振幅');
title('H[k]的幅度谱')
%画出H[k]的相频响应
subplot(4,2,4)
stem(angle(hk));
axis([0,10,-4,4]);
grid
xlabel('\omega/\pi');
ylabel('以弧度为单位的相位');
title('H[k]相位谱')
%画出G1[k]的幅频响应
subplot(4,2,5)
stem(abs(gk1));
axis([0,10,0,70]);
grid
xlabel('\omega/\pi');
ylabel('振幅');
title('G1[k]的幅度谱')
%画出G1[k]的相频响应
subplot(4,2,6)
stem(angle(gk1));
axis([0,10,-4,4]);
grid
xlabel('\omega/\pi');
ylabel('以弧度为单位的相位');
title('G1[k]相位谱')
%画出H1[k]的幅频响应
subplot(4,2,7)
stem(abs(hk1));
axis([0,10,0,200]);
grid
xlabel('\omega/\pi');
ylabel('振幅');
title('H1[k]的幅度谱')
%画出H1[k]的相频响应
subplot(4,2,8)
stem(angle(hk1));
axis([0,10,-4,4]);
grid
xlabel('\omega/\pi');
ylabel('以弧度为单位的相位');
title('H1[k]相位谱')
运行结果

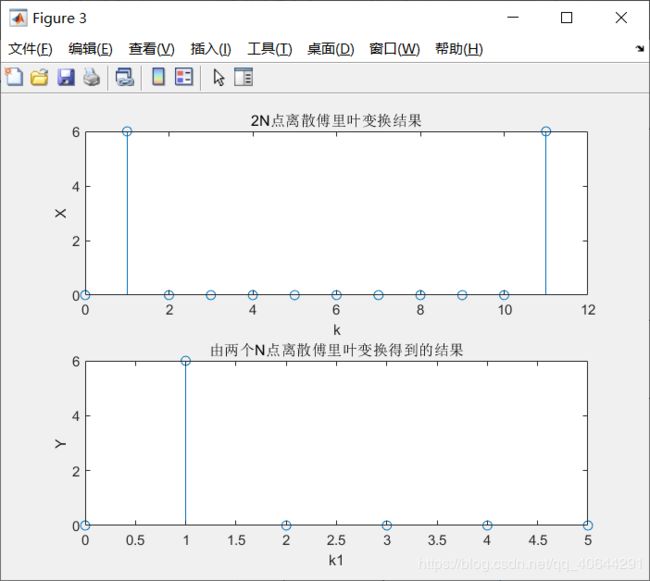
3.用两个N点离散傅里叶变换计算一个长度为2N的实数序列的2N点离散傅里叶变换,并将结果同直接使用一个2N点离散傳里叶变换得到的结果进行比较
设v[n]是长度为2N的实序列,V[n]表示它的2N点离散傅里叶变换。将长度为N的两个实序列g[n]和h[n]分别定义为
g [ n ] = v [ 2 n ] and h [ n ] = v [ 2 n + 1 ] , 0 ⩽ n < N g[n]=v[2 n] \text { and } h[n]=v[2 n+1], \quad 0 \leqslant n
并且G[k]和H[k]表示它们的N点离散傅里叶变换,则v[n]的2N点离散傅里叶变换V[k],可以自两个N点离散傅里叶变换G[A]和H[k]计算得到,即
V [ k ] = G [ ( k ) N ] + W 2 N k H [ ( k ) N ] , 0 ⩽ k ⩽ 2 N − 1 V[k]=G\left[(k)_{N}\right]+W_{2 N}^{k} H\left[(k)_{N}\right], \quad 0 \leqslant k \leqslant 2 N-1 V[k]=G[(k)N]+W2NkH[(k)N],0⩽k⩽2N−1
实现代码
设定原序列为x=cos(n*pi/6)
N=6; %给定N的值
n=0:2*N-1; %设定n的范围
x=cos(pi/6.*n); %给定序列x[n]
m=0:N-1; %设定m的范围
x1=cos(pi/6.*(2*m)); %取n为偶数时x[n]的值组成序列x1[n]
x2=cos(pi/6.*(2*m+1)); %取n为奇数时x[n]的值组成序列x2[n]
figure,
subplot(3,1,1)%指定位置1,绘制序列x[n]
stem(n,x);
xlabel('n'); %设定序列x[n]的横轴标注和纵轴标注
ylabel('x');
title('原序列x[n]')
subplot(3,1,2)%指定位置2,绘制序列x1[n]
stem(m,x1);
xlabel('m'); %设定序列x1[n]的横轴标注和纵轴标注
ylabel('x1');
title('取n为偶数时x[n]的值组成序列x1[n]')
subplot(3,1,3)%指定位置3,绘制序列x2[n]
stem(m,x2);
xlabel('m'); %设定序列x2[n]的横轴标注和纵轴标注
ylabel('x2');
title('取n为奇数时x[n]的值组成序列x2[n]')
k1=0:N-1; %设定k1的范围
k2=0:N-1; %设定k2的范围
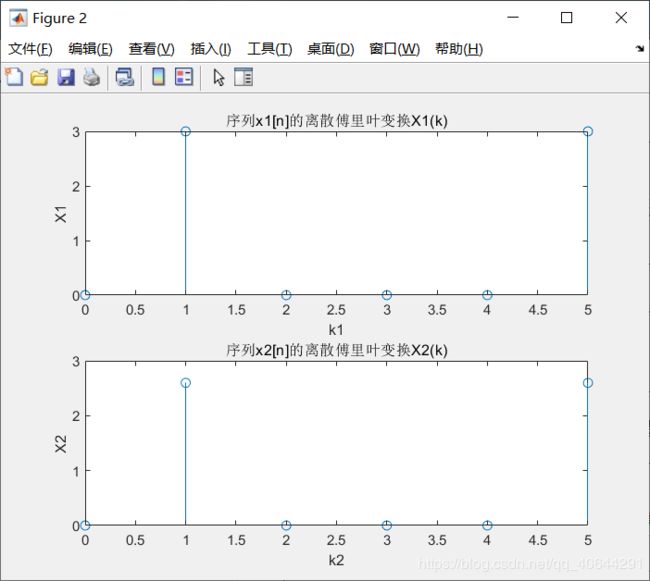
X1=fft(x1); %求序列x1[n]的离散傅里叶变换
X2=fft(x2); %求序列x2[n]的离散傅里叶变换
figure,
subplot(2,1,1)%指定位置1,绘制X1(k)
stem(k1,real(X1));
xlabel('k1'); %设定X1(k)的横轴标注和纵轴标注
ylabel('X1');
title('序列x1[n]的离散傅里叶变换X1(k)')
subplot(2,1,2) %指定位置2,绘制X2(k)
stem(k2,real(X2));
xlabel('k2'); %设定X2(k)的横轴标注和纵轴标注
ylabel('X2');
title('序列x2[n]的离散傅里叶变换X2(k)')
W=exp(-1i*pi/N).^k2; %给定W的值
Y=X1+X2.*W; %给定Y
X=fft(x); %求序列x[n]的离散傅里叶变换
k=0:2*N-1; %设定k的范围
figure,
subplot(2,1,1) %指定位置1,绘制X(k)
stem(k,real(X));
xlabel('k'); %设定X(k)的横轴标注和纵轴标注
ylabel('X');
title('2N点离散傅里叶变换结果')
subplot(2,1,2)%指定位置2,绘制Y(k)
stem(k1,real(Y));
xlabel('k1'); %设定Y(k)的横轴标注和纵轴标注
ylabel('Y');
title('由两个N点离散傅里叶变换得到的结果')
运行结果