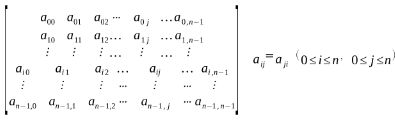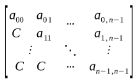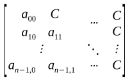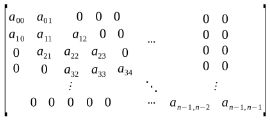【数据结构与算法】快速恶补图与矩阵压缩算法
开发工具与关键技术:数据结构与算法
作者:陈芝番
撰写时间:2020.4.26
目录
前言
1.图的定义
2.算法设计需要考虑什么呢?
3.遍历图的基本方法:
4.问题思考
5.最短路径问题解法
6.邻接矩阵
7.邻接矩阵存储结构定义
8.建立图的邻接矩阵
9.特殊矩阵的压缩存储
分析:
前言
图结构是一种比树型结构更为复杂的非线性结构,任意一个节点都可以有任意多个前驱和后继。图结构是一种重要的数据结构,对我们普遍的人来说,图是一种设计和规划等等,而图也可以是一个结构图,对图进行分析,验算,数据元素之间的关系。所谓数组,是有序的元素序列,用于存储多个相同类型数据的集合。
1.图的定义
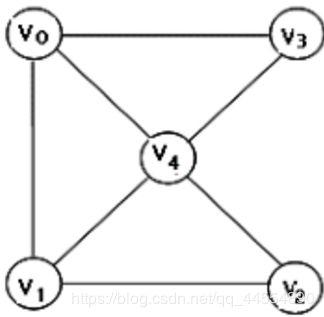
图是由顶点和边组成,顶点表示图的数据元素,边表示数据元素之间的关系。
图的遍历:从图中某一顶点出发遍历图中其余顶点,且使每一顶点仅被访问一次。
若图中表示边的顶点对是无序的,即称无向边,则图为无向图。
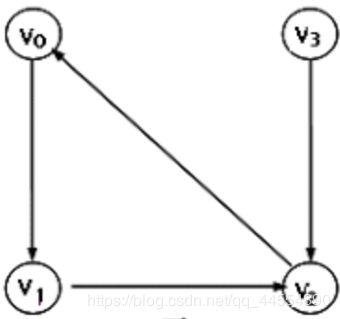
若图中表示变的顶点对是有序的,即称有向边,则图为有向图。
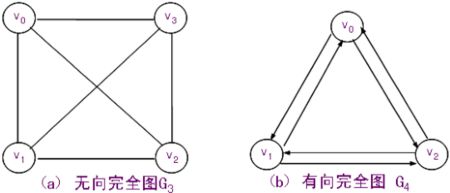
其中图又有完全图,稠密图,稀疏图。若无向图有1/2n(n-1)条边,即图中每对顶点之间都有一条边,即称该无向图为无向完全图。若有向图中有n(n-1)条孤,即图中每对顶点之间都有方向相反的两条孤。则称该有向图为有向完全图。有很少边的图或孤的图称为稀疏图,反之称为稠密图。
当然还有连通图,连通分量;强连通图,强连通分量;权,网等等。
图的存储结构比线性表和树的结构来说更为复杂,既要存储所有顶点的信息,又要存储顶点与顶点之间的所有关系,也就是边的信息。我们常说的“顶点的位置”和邻接点只是一个相对概念,图上任一顶点都可以看做初始顶点,任一顶点邻接点之间不存在次序关系。
2.算法设计需要考虑什么呢
需要考虑三个问题
- 算法的参数要指定访问的第一个顶点;
- 要考虑遍历路径可能出现的死循环问题;
- 要使一个顶点的所有邻接顶点按照某种次序被访问。
3.遍历图的基本方法
(1)深度优先搜索:
算法:
//从第i个顶点出发
Int visited[NAX_VEX]={0};
Void Dfs_m(Mgraph*G,int i){
Printf(“%3c”,G->vexs[i]);//访问顶点
visited[i]=1;
For(j=0;jarcs[i][j]==1)&&(!visited[j]))
Dfs_m(G,j);
} (2)广度优先搜索。
4.问题思考
从第i个顶点出发深度优先遍历以邻接表表示的图的算法
如下:
Typedef emnu {FALSE,TRUE}BOOLEAN;
BOOLEAN Visited[MAX_VEX];
Void DFS (ALGraph *G,int v)
{
linkNode*p;
Visited[v]=TRUE;
Visited(v);//访问顶点
P= G->AdjList[v].firstarc;
While(p!= NULL)
{
If(!Visited[p->adjvex])
{
DFS(G,P->ajdvex);
}
P=p->nextarc;
}
}5.最短路径问题解法
边上权值非负情形的单源最短路径问题
---Dijkstra算法
初始化s--{V0};
Dist[j]--Gn.arcs[0][j],path[j],--0或-1
{j=1,2,......,n-1}求出最短路径的长度:
Dist[k]--min{dist[i]},i(-V-s;
-SU{k};修改:
Dist[j]--min{dist[j],dist[k]+Gn.arcs[k][j]};
Path[j]--k;对于每一个j(-V-S;判断:
若S=V或也无顶点可加入到S中,则算法结束,否则转(1)。
所有顶点之间的最短路径
---Floyd算法
Void Floyd (int dis [n+1][n+1],int path[n+1][n+1],int n)
{
Int i,j,k;
For(k=1;k<=n;k++)
For(i = 1;i<=n;i++)
For(j=1;j<=n;j++)
If(dis[i][k]+dis[k][j]6.邻接矩阵
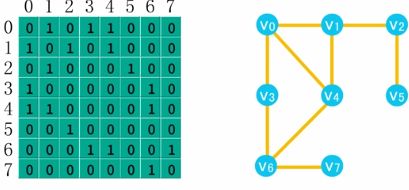
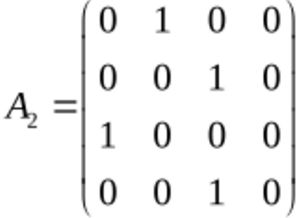
邻接矩阵采用两个数组来表示图,一个一维数组,存储图中所有顶点的信息,另一个是二维数组,即邻接矩阵,存储顶点之间的关系。
7.邻接矩阵存储结构定义
Typedef char VertexType;
Typedef int EdgeType;
//定义图结构,用邻接矩阵存储
Typedef struct {
VertexType vex[Max Vex];//顶点集合
EdgeType arc[Max Vex][MaxVex];//边集合
Int numVertex,numEdge;//图中实际的顶点数和边数
} MGraph;
8.建立图的邻接矩阵
建立无向图邻接矩阵算法描述如下:
Void Creat (MGraph*G)
{
Int i ,j,k;
Printf(“输入顶点数和边数:\n”);
Scanf(“%d,%d,&G->numVertex,&G->numEdge);
Getchar();
Printf(“输入顶点的集合:\n”);
//输入顶点信息
For(i=0;inumVertex;i++)
Scanf(“%c,&G->vex[i]);
For(i=0;inumVertex;i++)
For(j=0;jnumVertex;j++)
G->arc[i][j]=0;
Getchar();
For(k=0;knumEdge;k++)
{
Printf(“请输入边(i,j):\n”);
Scanf(“%d,%d”,&i,&j);
G->arc[i][j]=1;
G->arc[j][i]=1;
}
} 即算法GreatMgraph的时间复杂度是O(n^2)。
9.特殊矩阵的压缩存储
所谓特殊矩阵是指矩阵中值相同的元素或者零元素的分布有一定规律。如对称矩阵,三角矩阵和对角矩阵等。
- 对称矩阵
对于一个n阶矩阵A中的元素满足,ai = aj(0《i《n ,0《j 《n),即称A为对称矩阵。
压缩存储结构
假设用一个一维数组B[n(n+1)/2]来存储n阶对称矩阵A的压缩存储结构。即存储对应的关系如下:
- 三角矩阵
当一个方阵An*n的主对角线以上或下的所有元素皆为常数时,该矩阵称为三角矩阵。
紧接三角矩阵定义,三角矩阵有上三角矩阵和下三角矩阵两种。
上三角矩阵的特点是对角线下方(不包括主对角线)的元素均为常数C。
下三角矩阵的特点是对角线上方(不包括主对角线)的元素均为常数C。
三角矩阵与对称矩阵的压缩存储类似,对于上三角矩阵而言,应先存储完对角线上方的元素后,再存储对角线下方常量,因为是同一个常量,只需划分一个存储空间。
- 对角矩阵
所有非零元素集中在主对角线为中心的带状区域
除第0行和第n-1行是两个元素外,其他每行均为3个非零元素,因此需要存储的元素个数为2+2+3{n-2}=3n-2。将其压缩存储在B数组中,
由于这些特殊的矩阵元素有着一定的规律,在存储的时候为了节省存储空间,可以对这些矩阵进行压缩存储。所谓压缩存储就是为多个值相同的元素分配一个存储空间,对零元素不分配存储空间。
分析:
数组本身是线性表的推广,一维数组是一个向量形式的线性表,二维数组是一维数组组成的线性表。关于矩阵,它在科学计算领域等应用中,经常用到矩阵的概念,具有元素数目固定以及按下标关系有序排列等特点。基于压缩存储思想,矩阵中的相同数据元素(包括元素0)只存储一个。