第11章 电力系统的潮流计算
开式网络的电压和功率分布计算
- 11.1开式网络的电压和功率计算
- 11.1.1已知供电点电压和负荷节点功率时的计算方法
11.1开式网络的电压和功率计算
开式网络是电力网中结构最简单的一种,一般是由一个电源点通过辐射状网络向若干个负载节点供电.潮流计算的任务就是要根据给定的网络接线和其他已知条件,计算网络中的功率分布,功率损耗和未知的节点电压.
11.1.1已知供电点电压和负荷节点功率时的计算方法
下图所示网络中,供电点A通过馈电干线向负荷节点b,c,d供电,各负荷节点功率已知.如果节点d的电压也给定,就可以从节点d开始,利用同一点的电压和功率计算第三段线路的电压降落和功率损耗,得到节点c的电压,并算出第二段线路末端的功率.然后依次计算第二段线路和第一段线路的电压降落和功率损耗,一次性地求得解答.但是实际的情况并不这么简单,多数的情况是已知电源点电压和负荷节点的功率,要求确定各负荷点电压和网络中的功率分布.在这种情况下,可以采取近似的方法通过迭代计算求得满足一定精度的答案.
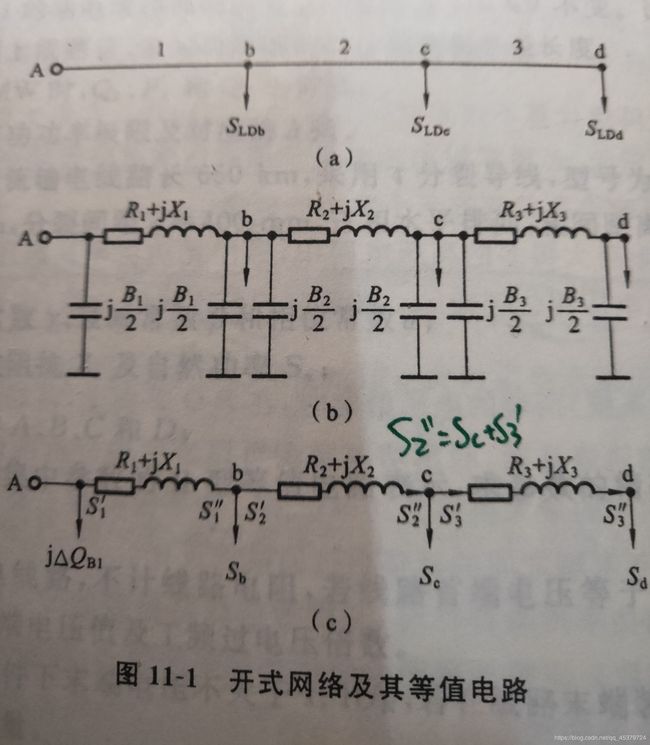
在进行电压和功率分布计算以前,先要对网络的等值电路[见图11-1(b)]作些简化处理,具体的做法是,将输电线等值电路中的电纳支路都分别用额定电压 U N U_N UN下的充电功率代替,这样,对每段线路的首端和末端的节点都分别加上该段线路充电功率的一半。
Δ Q B i = − 1 2 B i U N 2 ( i = 1 , 2 , 3 ) \Delta Q_{Bi}=-\frac{1}{2}B_iU^2_N(i=1,2,3) ΔQBi=−21BiUN2(i=1,2,3)
为简化起见,再将这些充电功率分别与相应节点的负荷功率合并,便得
S b = S L D b + j Δ Q B 1 + j Δ Q B 2 = P L D b + j [ Q L D b − 1 2 ( B 1 + B 2 ) U N 2 ] = P b + j Q b S_b=S_{LDb}+j\Delta Q_{B1}+j\Delta Q_{B2}=P_{LDb}+j[Q_{LDb}-\frac{1}{2}(B_1+B_2)U^2_N]=P_b+jQ_b Sb=SLDb+jΔQB1+jΔQB2=PLDb+j[QLDb−21(B1+B2)UN2]=Pb+jQb
S c = S L D c + j Δ Q B 2 + j Δ Q B 3 = P L D c + j [ Q L D c − 1 2 ( B 2 + B 3 ) U N 2 ] = P c + j Q c S_c=S_{LDc}+j\Delta Q_{B2}+j\Delta Q_{B3}=P_{LDc}+j[Q_{LDc}-\frac{1}{2}(B_2+B_3)U^2_N]=P_c+jQ_c Sc=SLDc+jΔQB2+jΔQB3=PLDc+j[QLDc−21(B2+B3)UN2]=Pc+jQc
S d = S L D d + j Δ Q B 3 = P L D d + j ( Q L D d − 1 2 B 3 U N 2 ) = P b + j Q d S_d=S_{LDd}+j\Delta Q_{B3}=P_{LDd}+j(Q_{LDd}-\frac{1}{2}B_3U^2_N)=P_b+jQ_d Sd=SLDd+jΔQB3=PLDd+j(QLDd−21B3UN2)=Pb+jQd
习惯上称 S b , S c , S d S_b,S_c,S_d Sb,Sc,Sd为电力网的运算负荷.这样,我们就把原网络简化为由三个集中的阻抗元件相串联,而在四个节点(包括供电点)接有集中负荷的等值网络[见图11-1©].
针对图11-1©的等值网络将按以下两个步骤进行电压和功率分布的计算.
第一步,从离电源点最远的节点d开始,利用线路额定电压,逆着功率传送的方向依次算出各段线路阻抗中的功率损耗和功率分布。对于第三段线路
S 3 ′ ′ = S d , Δ S L 3 = P ′ ′ 3 2 + Q ′ ′ 3 2 U N 2 ( R 3 + j X 3 ) , S 3 ′ = S 3 ′ ′ + Δ S L 3 S''_3=S_d,\Delta S_{L3}=\frac{P''{_3}{^2}+Q''{_3}{^2}}{U^2_N} (R_3+jX_3),S'_3=S''_3+\Delta S_{L3} S3′′=Sd,ΔSL3=UN2P′′32+Q′′32(R3+jX3),S3′=S3′′+ΔSL3
对于第二段电路
S 2 ′ ′ = S c + S 3 ′ , Δ S L 2 = P ′ ′ 2 2 + Q ′ ′ 2 2 U N 2 ( R 2 + j X 2 ) , S 2 ′ = S 2 ′ ′ + Δ S L 2 S''_2=S_c+S'_3,\Delta S_{L2}=\frac{P''{_2}{^2}+Q''{_2}{^2}}{U^2_N} (R_2+jX_2),S'_2=S''_2+\Delta S_{L2} S2′′=Sc+S3′,ΔSL2=UN2P′′22+Q′′22(R2+jX2),S2′=S2′′+ΔSL2
同样地可以算出第一段线路的功率 S 1 ′ S'_1 S1′.
第二步,利用第一步求得的功率分布,从电源点开始,顺着功率传送方向,依次计算各段线路的电压降落,求出各节点电压。先计算电压 U b U_b Ub,有
Δ U A b = P 1 ′ R 1 + Q 1 ′ X 1 U A , δ U A b = P 1 ′ X 1 − Q 1 ′ R 1 U A \Delta U_{Ab}=\frac{P'_1R_1+Q'_1X_1}{U_A},\delta U_{Ab}=\frac{P'_1X_1-Q'_1R_1}{U_A} ΔUAb=UAP1′R1+Q1′X1,δUAb=UAP1′X1−Q1′R1
U b = ( U A − Δ U A b ) 2 + ( δ U A b ) 2 U_b=\sqrt{(U_A-\Delta U_Ab)^2+(\delta U_{Ab})^2} Ub=(UA−ΔUAb)2+(δUAb)2
接着用 U b U_b Ub及 S 2 ′ S'_2 S2′计算 U c U_c Uc,最后用 U c U_c Uc及 3 ′ '_3 3′计算 U d U_d Ud.
通过以上两个步骤便完成了第一轮的计算.为了提高计算精度,可以重复以上的计算,在计算功率损耗时可以利用上一轮第二步所求得的节点电压.
上述计算方法也适用于由一个供电点通过辐射状网络向任意多个负荷节点供电的情况.辐射状网络即是树状网络,或简称为树.供电点即是树的根节点,树中不存在任何闭合回路号功率的传送方向是完全确定的,任一条支路都有确定的始节点和终节点.除根节点外,树中的节点可分为叶节点和非叶节点两类.叶节点只同一 条支路联接,且为该支路的终节点,非叶节点同两条或两条以上的支路联接,它作为一条支路的终节点,又兼作另一条或多条支路的始节点.对于图11-2所示的网络,A是供电点,即根节点,节点b,c和e为非叶节点,节点d,h,f和g为叶节点.
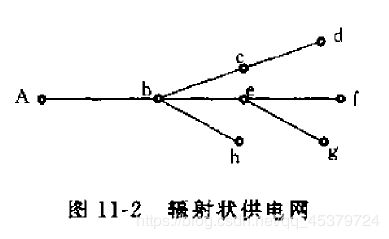
根据前述计算步骤,第一步,从与叶节点联接的支路开始,该支路的末端功率即等于叶节点功率,利用这个功率和对应的节点电压计算支路功率损耗,求得支路的首端功率凸当以某节点为始节点的各支路都计算完毕后,便想像将这些支路都拆去,使该节点成为新的叶节点,其节点功率等于原有的负荷功率与以该节点为始节点的各支路首端功率之和.于是计算便可延续下去,直到全部支路计算完毕.这一步骤的计算公式如下:
S ′ ′ i j ( k ) = S j ( k ) + ∑ m ∈ N j S ′ j m ( k ) {S''}_{ij}^{(k)}={S}_{j}^{(k)}+\sum\limits_{m\in N_j}{S'}_{jm}^{(k)} S′′ij(k)=Sj(k)+m∈Nj∑S′jm(k)
Δ S i j ( k ) = P ′ ′ i j ( k ) 2 + Q ′ ′ i j ( k ) 2 U j ( k ) 2 ( r i j + j x i j ) \Delta{S}_{ij}^{(k)}=\frac{{P''}_{ij}^{(k)2}+{Q''}_{ij}^{(k)2}}{{U}_{j}^{(k)2}}(r_{ij}+jx_{ij}) ΔSij(k)=Uj(k)2P′′ij(k)2+Q′′ij(k)2(rij+jxij)
S ′ i j ( k ) = S ′ ′ i j ( k ) + Δ S i j ( k ) {S'}_{ij}^{(k)}={S''}_{ij}^{(k)}+{\Delta S}_{ij}^{(k)} S′ij(k)=S′′ij(k)+ΔSij(k)
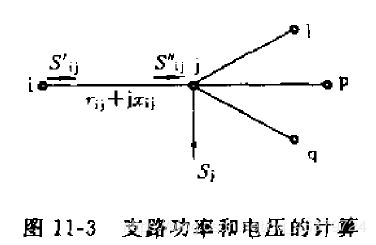
式中, N j Nj Nj为以j为始节点的支路的终节点集,对图11-3所示的情况. N j N_j Nj={l,p,q}.若j为叶节点,则 N j N_j Nj为空集.k为迭代计数.
对于第一轮的迭代计算,节点电压取为给定的初值,—般为网络的额定电压。
第二步,利用第一步所得的支路首端功率和本步骤刚算出的本支路始节点的电压(对电源点为已知电压),从电源点开始逐条支路进行计算,求得各支路终节点的电压,其计算公式为
U j ( k + 1 ) = ( U i ( k + 1 ) − P ′ i j ( k ) r i j + Q ′ i j ( k ) x i j U i ( k + 1 ) ) + ( P ′ i j ( k ) x i j − Q ′ i j ( k ) r i j U i ( k + 1 ) ) {U}_j^{(k+1)}=\sqrt{ ({U}_i^{(k+1)}-\frac{{P'}_{ij}^{(k)}r_{ij}+{Q'}_{ij}^{(k)}x_{ij}} {{U}_{i}^{(k+1)}}) +( \frac{{P'}_{ij}^{(k)}x_{ij}- {Q'}_{ij}^{(k)}r_{ij}} {{U}_{i}^{(k+1)}} )} Uj(k+1)=(Ui(k+1)−Ui(k+1)P′ij(k)rij+Q′ij(k)xij)+(Ui(k+1)P′ij(k)xij−Q′ij(k)rij)
上述计算公式都很简单,对于规模不大的网络,可手工计算,精度要求不很高时,作一 轮计算即可。若已给定容许误差为ε,则以
m a x { ∣ U i ( k + 1 ) − U i ( k ) ∣ } < ε max\{|{U}_{i}^{(k+1)}-{U}_{i}^{(k)}|\}<ε max{∣Ui(k+1)−Ui(k)∣}<ε
作为计算收敛的判据.
对于规模较大的网络,最好应用计算机进行计算.在迭代计算开始之前,先要处理好支路的计算顺序问题口现在介绍两种确定支路计算顺序的方法.
第一种方法是,按与叶节点联接的支路排序,并将已排序的支路拆除,在此过程中将不断出现新的叶节点,而与其联接的支路又加入排序行列.这样就可以全部排列好从叶节点向电源点计算功率损耗的支路顺序。其逆序就是进行电压计算的支路顺序口以图11-2的网络为例,设从节点d开始,选支路cd, 作为第一条支路.拆去cd, 节点c就变成叶节点,支路bc便作为第二条支路.拆去bc时没有出现新的叶节点.接
着排上ef和eg支路.拆去该两条支路,e成为叶节点,于是排上be支路,接下去是bh和Ab支路.当然,从节点f开始,按ef,eg,be,bh,cd,bc,Ab排序也是一种可行的方案.由此可见,同一排序原则可以有多种不同的实现方案.顺便指出,在节点优化编号中,动态地按联接支路数等千1进行节点编号,也能得到与此完全等效的结果.
第二种是逐条追加支路的方法.首先从根节点(电源点)开始接出第一条支路,引出一个新节点,以后每次追加的支路都必须从已出现的节点接出,遵循这个原则逐条追加支路,直到全部支路追加完毕.所得到的支路追加顺序即是进行电压计算的支路顺序,其逆序便是功率损耗计算的支路顺序.对图11-2所示的网络,Ab,bc,cd,bh,be,ef,eg就是一种可行的顺序。显而易见,可行的排序方案也不止一种.
无论采取哪一种支路排序方法,其程序实现都不存在什么困难.
按上述方法进行开式网络的潮流计算,不需要形成节点导纳矩阵,不必求解高阶方程组,计算公式简单,收敛迅速,十分实用.
例11-1 开式网络如图11-2所示。各支路阻抗和节点负荷功率如下.

解 先确定损耗功率计算的支路顺序为cd,bc,ef,be,bh,ab每一轮计算的第一步是按式(11-1)~(11-3)依上列支路顺序计算各支路的功率损耗和功率分布;第二步用公式(11-4)按上列相反的顺序作电压计算.计算结果如表11-1,表11-2所示.
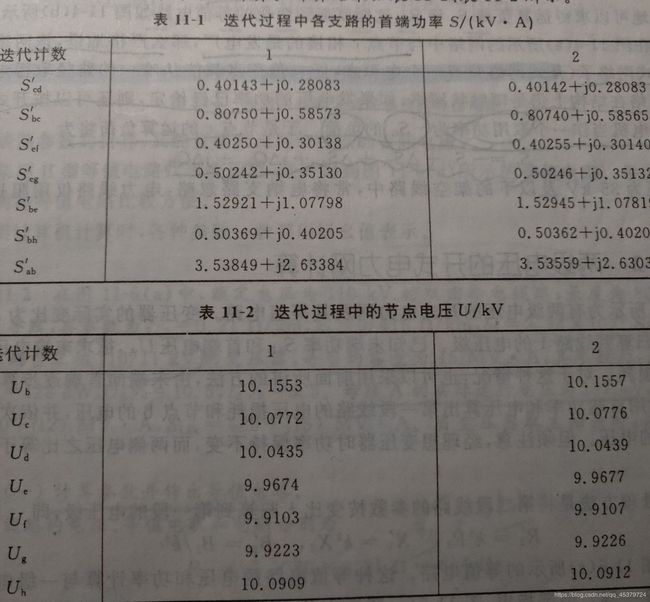
经两轮迭代计算,各节点电压误差均在0.001kV以内,计算到此结束.
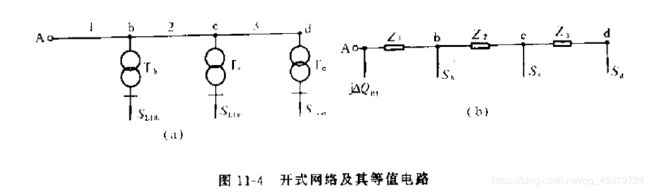
实 际 的 配 电 网 中 , 负 荷 并 不 都 接 在 馈 电 干 线 上 , 在 图 11 − 4 ( a ) 所 示 的 网 络 中 , 节 点 b 、 c 和 d 都 接 有 降 压 变 压 器 , 并 且 已 知 其 低 压 侧 的 负 荷 功 率 分 别 为 S L D b , S L D c , S L D d . 在 这 种 情 况 下 , 应 先 将 负 荷 功 率 S L D 加 上 相 应 的 变 压 器 的 绕 组 损 耗 Δ S T 和 励 磁 损 耗 Δ S 0 , 以 求 得 变 压 器 高 压 侧 的 负 荷 功 率 S L D ′ . 例 如 , 对 于 节 点 b , 有 实际的配电网中,负荷并不都接在馈电干线上,在图11-4(a)所示的网络中,节点b、c和d都接有降压变压器,并且已知其低压侧的负荷功率分别为S_{LDb},S_{LDc},S_{LDd}.在这种情况下,应先将负荷功率S_{LD}加上相应的变压器的绕组损耗\Delta S_T和励磁损耗\Delta S_0,以求得变压器高压侧的负荷功率S'_{LD}.例如,对于节点b,有 实际的配电网中,负荷并不都接在馈电干线上,在图11−4(a)所示的网络中,节点b、c和d都接有降压变压器,并且已知其低压侧的负荷功率分别为SLDb,SLDc,SLDd.在这种情况下,应先将负荷功率SLD加上相应的变压器的绕组损耗ΔST和励磁损耗ΔS0,以求得变压器高压侧的负荷功率SLD′.例如,对于节点b,有
S L D b ′ = S L D b + Δ S T b + Δ S 0 b S'_{LDb}=S_{LDb}+\Delta S_{Tb}+\Delta S_{0b} SLDb′=SLDb+ΔSTb+ΔS0b
式中
Δ S T b = P L D d 2 + Q L D d 2 U N 2 ( R T b + j X T b ) ; Δ S 0 b = Δ P 0 b + j I 0 % 100 S N b \Delta S_{Tb}=\frac{ P^2_{LDd}+Q^2_{LDd} }{U^2_N}(R_Tb+jX_Tb);\Delta S_{0b}=\Delta P_{0b}+j\frac{I_0\%}{100}S_{Nb} ΔSTb=UN2PLDd2+QLDd2(RTb+jXTb);ΔS0b=ΔP0b+j100I0%SNb
然后再按照前面所说的方法,加上节点b所接线路1和2的电容功率的一半,便得到电力网在节点b的运算负荷为
S b = S L D b ′ + j Δ Q B 1 + j Δ Q B 2 S_b=S'_{LDb}+j\Delta Q_{B_1}+j\Delta Q_{B_2} Sb=SLDb′+jΔQB1+jΔQB2
同样地可以求得运算负荷 S c S_c Sc和 S d S_d Sd,这样就得到简化的等值电路如图11-4(b)所示.
如果在图11-4(a)的网络中与节点c相接的是发电厂,严格地讲,该网络已不能算是开式网络了(开式网络只有一个电源点,任一负荷点只能从唯一的路径取得电能).但是,该网络在结构上仍是辐射状网络,如果发电厂的功率已经给定,还可以按开式网络处理,把发电机当做是一个取用功率为- S G S_G SG七的负荷。于是节点c的运算负荷将为
S c = − S G + Δ S T c + Δ S 0 c + j Δ Q B 2 + j Δ Q B 3 S_c=-S_G+\Delta S_{Tc}+\Delta S_{0_c}+j\Delta Q_{B_2}+j\Delta Q_{B_3} Sc=−SG+ΔSTc+ΔS0c+jΔQB2+jΔQB3
电压为35kV及以下的架空线路中,常将电纳支路忽略,电力线路仅用阻抗元件代表.