总结一下最短路径的迪杰斯特拉算法(Dijkstra)的基本内容以及用邻接表优化
前面转了两篇博客说了一下这个迪杰斯特拉算法,现在自己尝试总结一下。
先上一个百度百科的定义:迪杰斯特拉算法
--------------------------------------------------------------------------------------------------------分割线----------------------------------------------------------------------------------------------------------------
首先,迪杰斯特拉算法是用来解决单源最短路经问题的,主要是通过边的松弛来实现。
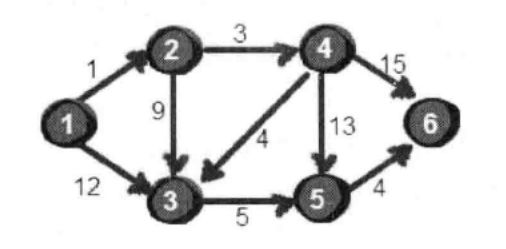
我们来看这个问题:
这个问题求得是从1号顶点到达所有其他顶点的最短距离,我们用邻接矩阵来存储这个图,如下:
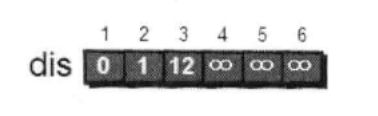
我们用一个dis数组来存储从一号顶点到其他各个顶点的初始路径,如图
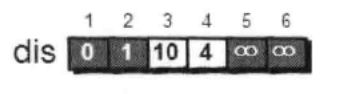
先找一个离一号顶点最近的顶点,通过dis我们知道最近的顶点是2号顶点,从第2个顶点有两条边是2-->3和2-->4。先通过2-->3这个边看能否是从1到3的路程变短,也就是比较dis[3]与dis[2]+map[2][3]的大小,很明显dis[3]=12,而dis[2]+map[2][3]=10,所以我们把dis[3]的值更新为10,这个过程就是我们所说的“松弛”,同样对于2-->4,dis[4]的初始值为无穷大,而dis[2]+dis[2][4]=4,所以我们把dis[4]的值松弛为4,经过这一个松弛后,dis变成了:
把已经找过的点进行标记,然后在剩下的3,4,5,6顶点钟找出离1号顶点最近的顶点,很明显最近的是4,然后根据上面的思路继续进行松弛,一直松弛到边完,这时dis变为
整个过程用完整的代码来表示如下:
#include
#include
#include
#include
#include
#include
#include
#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int inf=1<<29;
int main()
{
int map[10][10],t1,t2,t3,min,u,n,m;
int dis[10];
int vis[10];
scanf("%d%d",&n,&m);
//初始化
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
if(i==j)
map[i][j]=0;
else
map[i][j]=inf;
//读入边
for(int i=1; i<=m; i++)
{
scanf("%d%d%d",&t1,&t2,&t3);
map[t1][t2]=t3;
}
//初始化dis数组,表示1号顶点到其余各个顶点的最短路程
for(int i=1; i<=n; i++)
dis[i]=map[1][i];
//初始化vis
for(int i=1; i<=n; i++)
vis[i]=0;
vis[1]=1;//标记起始点1已经被访问过
//迪杰斯特拉算法(Dijkstra)的核心内容
for(int i=1; i<=n-1; i++) //因为松弛的是边数,所以是n-1
{
min=inf;
for(int j=1; j<=n; j++)
{
if(vis[j]==0&&dis[j] 输入:
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4输出:
0 1 8 4 13 17利用邻接表,我们可以把时间复杂度优化到O(M+N)logN,以下是用邻接表来优化这个算法的代码:
#include
#include
#include
#include
#include
#include
#include
#include
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int inf=0x3f3f3f3f;
int u[10],v[10],w[10],first[10],next[10],dist[10],vis[10],n,m,k,minn;
int main()
{
scanf("%d%d",&n,&m);
//初始化
for(int i=1; i<=n; i++)
first[i]=-1;
//读入边
mem(dist,inf);
for(int i=1; i<=m; i++)
{
scanf("%d%d%d",&u[i],&v[i],&w[i]);
next[i]=first[u[i]];
first[u[i]]=i;
if(u[i]==1)
dist[v[i]]=w[i];//初始化dis数组,表示1号顶点到其余各个顶点的最短路程
}
//初始化vis
for(int i=1; i<=n; i++)
vis[i]=0;
vis[1]=1;//标记起始点1已经被访问过
dist[1]=0;
//迪杰斯特拉算法(Dijkstra)的核心内容
for(int i=1; i<=n-1; i++)
{
minn=inf;
for(int j=1; j<=n; j++)
{
if(vis[j]==0&&dist[j]