排序方法详解与JavaScript实现 - 直接插入、shell排序、直接选择、堆排、冒泡、快排、归并、基数
排序方法总结 -- 排序过程
目录
直接插入
shell 排序
直接选择排序
堆排序
冒泡排序
快速排序
归并排序
基数排序
各种排序算法的稳定性,时间复杂度,空间复杂度总结:
| 类别 | 排序方法 | 平均 | 最好 | 最坏 | 辅助存储 | 稳定性 |
|---|---|---|---|---|---|---|
| 插入排序 | 直接插入 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| shell排序 | O(n^1,3) | O(n) | O(n^2) | O(1) | 不稳定 | |
| 选择排序 | 直接选择 | O(n^2) | O(n^2) | O(n^2) | O1) | 不稳定 |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 | |
| 交换排序 | 冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 快速排序 | O(nlog2n) | O(nlog2n) | O(n2) | O(nlog2n) | 不稳定 | |
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | 稳定 | |
| 基数排序 | O(d(r+n)) | O(d(r+n)) | O(d(r+n)) | O(rd+n) | 稳定 |
直接插入
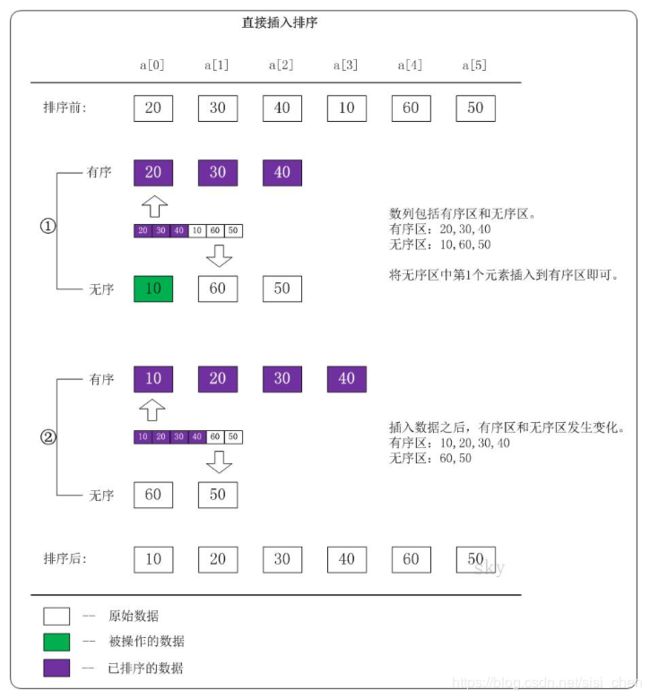
直接插入排序的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表。
开始时有序表中只包含1个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,将它插入到有序表中的适当位置,使之成为新的有序表,重复n-1次可完成排序过程。
JavaScript代码:
const insertSort = function (arr) {
var len = arr.length
var j,temp
for(let i = 0; i < len; i++) {
j = i - 1
temp = arr[i]
while( j >= 0 && arr[j] > temp) {
arr[j + 1] = arr[j]
j --
}
arr[j + 1] = temp
}
return arr
}shell 排序
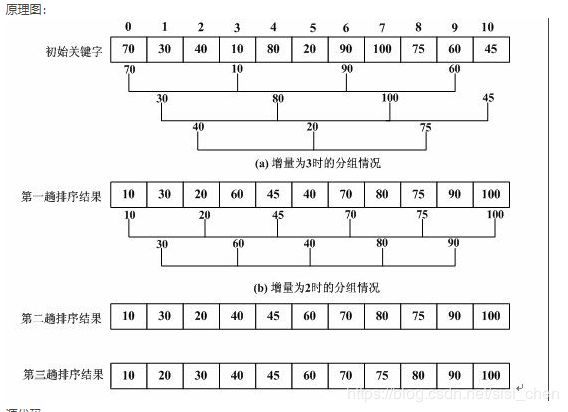
shell排序的基本思想是:
-
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。
-
所有距离为dl的倍数的记录放在同一个组中。
-
先在各组内进行直接插入排序;
-
取第二个增量d2
JavaScript代码:
const shellSort = function (arr) {
var gap = 1
var len = arr.length
//动态规划步长
while (gap > len/3) {
gap = gap*3 + 1
}
//步长组循环
for(gap; gap > 0; gap = Math.floor(gap/3)) {
//同步长循环
for(i = gap; i < len; i++) {
var temp = arr[i]
var j
//比较、并将数据后移
for(j = i - gap; j >= 0 && arr[j] > temp; j-=gap) {
arr[j + gap] = arr[j]
}
arr[j + gap] = temp
}
}
return arr
}直接选择排序
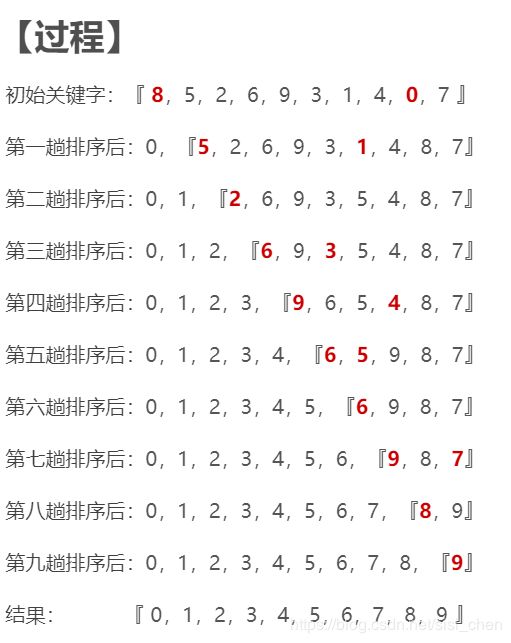
直接选择排序的基本思想:每一趟从待排序的数据元素中选出最小(最大)的元素,顺序放在待排序的数列最前,直到全部待排序的数据元素全部排完。
JavaScript代码:
const selectionSort = function (arr) {
var len = arr.length
for(let i = 0; i < len; i++) {
var min = i
for(let j = i + 1; j < len; j++) {
if(arr[min] > arr[j]) {
min = j
}
}
[arr[i],arr[min]] = [arr[min],arr[i]]
}
return arr
}
堆排序
堆分为最大堆和最小堆,其实就是完全二叉树。
最大堆要求节点的元素都要不小于其孩子,最小堆要求节点元素都不大于其左右孩子,两者对左右孩子的大小关系不做任何要求。(基本要求)
堆排序算法:每次都取堆顶的元素,将其放在序列最后面,然后将剩余的元素重新调整为最大堆,依次类推,最终得到排序的序列。
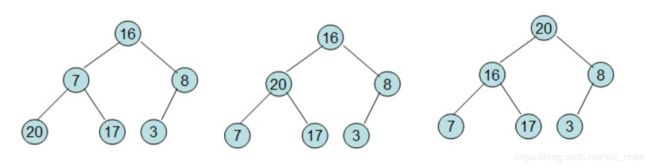
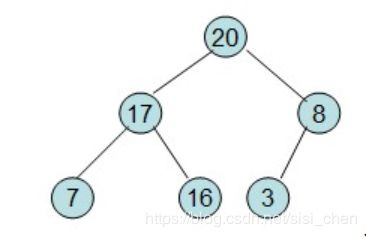
举例:给定一个列表 arr = [16,7,3,20,17,8],对其进行排序:
第一步:构建完全二叉树:
第二步:初始化最大堆(满足基本条件:节点的元素都要不小于其孩子):
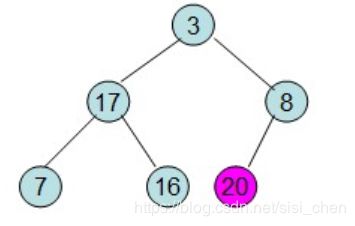
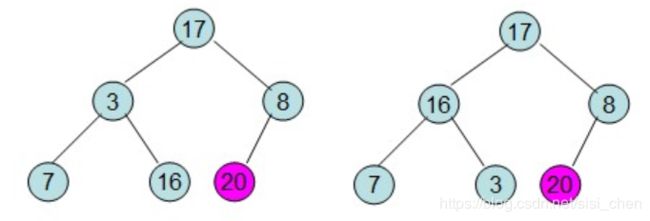
第三步:堆排序开始(取堆顶的元素,将其放在序列最后面,再调整为最大堆):
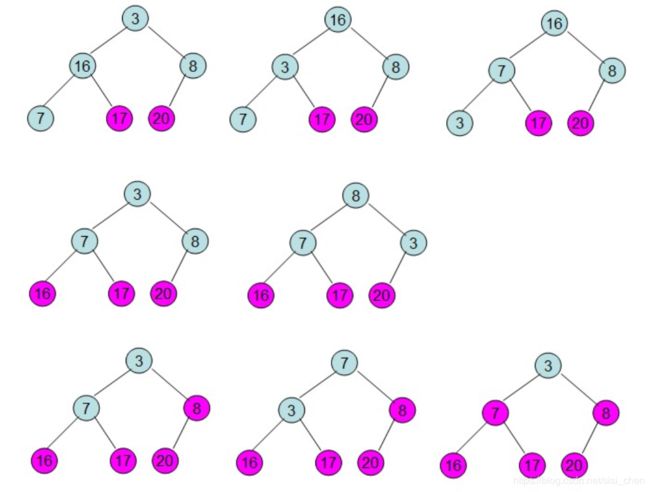
重复直到排序结束:
JavaScript代码:
// 调整堆
const adjustHeap = function(arr,fatherIndex,length) {
// 左子节点索引
var childIndex = fatherIndex * 2 + 1
// 保存父节点值
var temp = arr[fatherIndex]
while (childIndex <= length) {
// 判断左右节点,取最大子节点索引
if(childIndex + 1 <= length && arr[childIndex + 1] > arr[childIndex]) {
childIndex++
}
// 父节点大于子节点值直接跳出循环
if(temp >= arr[childIndex]) {
break
}
arr[fatherIndex] = arr[childIndex]
fatherIndex = childIndex
childIndex = childIndex * 2 + 1
}
arr[fatherIndex] = temp
}
// 堆排序
const heapSort = function (arr) {
var len = arr.length;
// 初始化最大堆
for (let i = Math.floor(len/2) - 1; i >= 0; i--) {
adjustHeap(arr,i,len-1)
console.log(arr)
}
for(let i = len-1; i >= 0; i--) {
[arr[0],arr[i]] = [arr[i],arr[0]]
adjustHeap(arr,0,i-1)
}
return arr
}冒泡排序
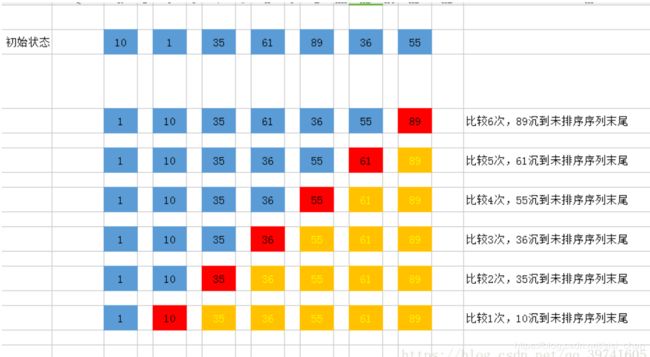
冒泡排序的基本思想:比较两两相邻的关键字,如果反序则进行交换,直到没有反序的为止。
JavaScript代码:
const bubbleSort = function (arr) {
var len = arr.length - 1
for(let i = 0; i < len; i++) {
for(let j = 0; j < len - i; j++) {
if(arr[j] > arr[j + 1]) {
[arr[j],arr[j + 1]] = [arr[j + 1],arr[j]]
}
}
}
return arr
}快速排序
由冒泡排序演变而来,比冒泡高效,之所以高效是因为使用了分治法。
基本思想:在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成了两个部分。
JavaScript代码:
const quickSort = function (arr) {
var len = arr.length
if(len < 2) {
return arr
}
var stand = arr[0]
var mins = [], maxs = []
for(let i = 1; i < len; i++) {
if(arr[i] < stand) {
mins.push(arr[i])
}
else {
maxs.push(arr[i] )
}
}
//递归
return [...quickSort(mins), stand, ...quickSort(maxs)]
}
//三路快排
const quickThreeSort = function (arr) {
var len = arr.length
if(len < 2) {
return arr
}
var stand = arr[0]
var mins = [], maxs = [], quas = []
for(let val of arr) {
if(val < stand) {
mins.push(val)
}
else if(val === stand) {
quas.push(val)
}
else {
maxs.push(val)
}
}
//递归
return [...quickSort(mins), ...quas, ...quickSort(maxs)]
}归并排序
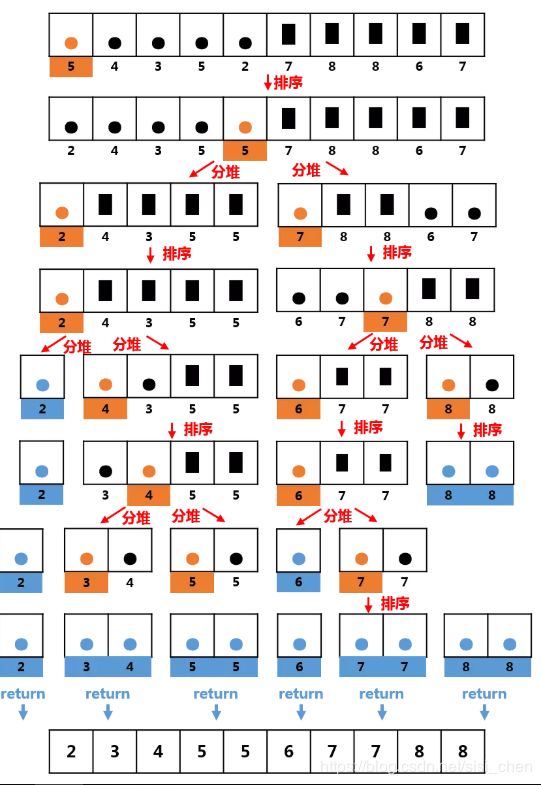
将两个的有序数列合并成一个有序数列,我们称之为"归并"。 归并排序就是利用归并思想对数列进行排序。根据具体的实现,归并排序包括"从上往下"和"从下往上"2种方式。
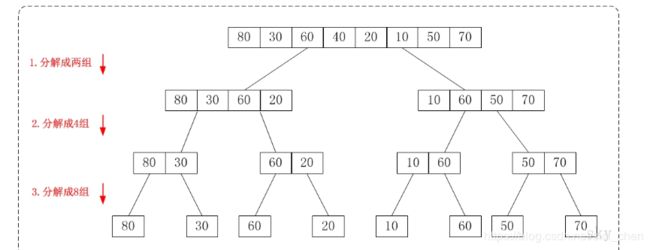
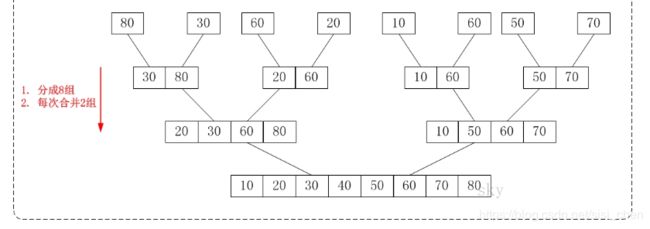
从下往上的归并排序:将待排序的数列分成若干个长度为1的子数列,然后将这些数列两两合并;得到若干个长度为2的有序数列,再将这些数列两两合并;得到若干个长度为4的有序数列,再将它们两两合并;直接合并成一个数列为止。这样就得到了我们想要的排序结果。
JavaScript代码:
const merge = function (left,right) {
let resArr = []
while(left.length && right.length) {
if(left[0] < right[0]) {
resArr.push(left.shift())
} else {
resArr.push(right.shift())
}
}
return resArr.concat(left,right)
}
const mergeSort = function (arr) {
var len = arr.length
if(len < 2) {
return arr
}
var mid = Math.floor(len/2)
var left = arr.slice(0,mid)
var right = arr.slice(mid)
return merge(mergeSort(left), mergeSort(right))
}基数排序
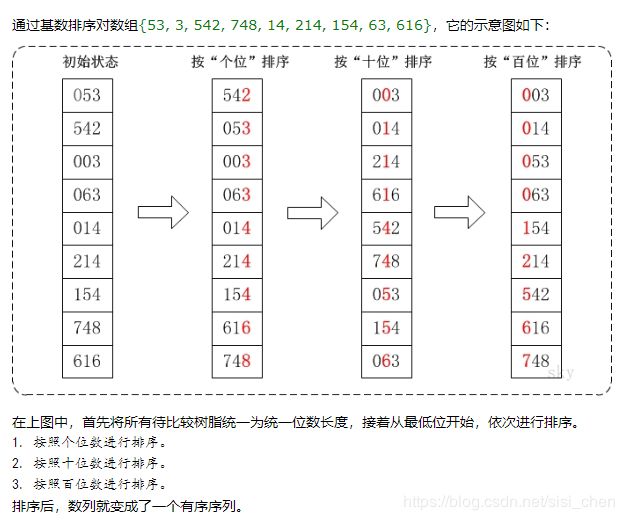
基数排序(Radix Sort)是桶排序的扩展,它的基本思想是:将整数按位数切割成不同的数字,然后按每个位数分别比较。 具体做法是:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。