算法导论（二）——排序算法整理

算法导论（二）——排序算法整理

【主要参考资料：MIT算法导论视频，《数据结构，算法与应用，c++语言描述》】

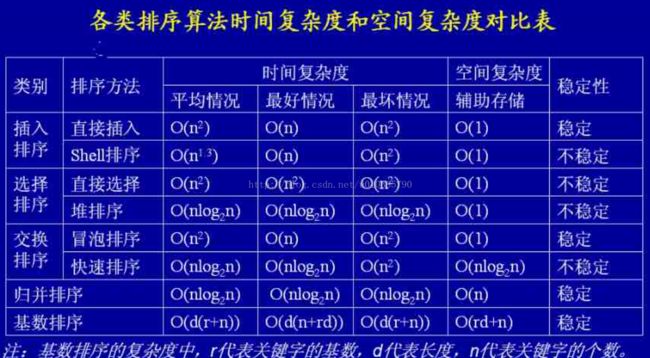
排序算法：

1.    时间开销

•排序的时间开销可用算法执行中的数据比较次数与数据移动次数来衡量。

•算法运行时间代价的大略估算一般都按平均情况进行估算。对于那些受对象初始排列及对象个数影响较大的，需要按最好情况和最坏情况进行估算

2.    空间开销

算法执行时所需的附加存储。

3.    基于比较排序算法时间下限

n个元素，总共有n!种排列，每进行一次比较都会减掉一半的可能性。比较次数最少为

，

因为，故

或者用决策树分析，每个具有n!的外部节点的二叉树的平均高度为，故每个基于比较的排序算法的平均复杂度为。

1.    插入排序

思想：每次将一个待排序的数据按照其关键字的大小插入到前面已经排序好的数据中的适当位置，直到全部数据排序完成。

复杂度： O(n2) O(n) O(n2) （最坏 最好 平均） O(1)

稳定性：稳定, 每次都是在前面已排好序的序列中找到适当的位置，只有小的数字会往前插入，所以原来相同的两个数字在排序后相对位置不变。

【希尔排序不稳定】

 

改进参考：http://www.cnblogs.com/heyuquan/p/insert-sort.html

①折半（二分）插入排序：从无序区中取出元素，使用二分查找算法在有序区中查找要插入的位置。 O(n^2)

②希尔排序：

思想：希尔排序根据增量值对数据按下表进行分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整体采用直接插入排序得到有序数组，算法终止。

使得输入大体上有序，增量为一个数组。先取整数dt（）作为第一个增量，把输入分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2（）重复上述的分组和排序，直至所取的增量dt=1(dt，即所有记录放在同一组中进行直接插入排序为止。

复杂度：O(n2) O(n) O(n1.3)（最坏，最好，平均）O(1)

稳定性; 不稳定 因为是分组进行直接插入排序，原来相同的两个数字可能会被分到不同的组去，可能会使得后面的数字会排到前面，使得两个相同的数字排序前后位置发生变化。

 

2.    归并排序

思想：分治算法，首先递归将原始数组划分为若干子数组，对每个子数组进行排序。然后将排好序的子数组递归合并成一个有序的数组。

时间复杂度：最坏:O(nlog2n) 最好: O(nlog2n) 平均: O(nlog2n)   O(n)

稳定性：稳定

①直接归并排序（二路归并排序）：将每两个相邻大小为1的子序列归并，然后将每两个相邻的大小为2的子序列归并，如此反复。

②自然归并排序，找出已有的有序段（【i】>【i+1】，则i为断点），进行归并。

③合并的时候，大部分算法实现都是新申请数组，所需空间较大，使用手摇法来实现额外空间复杂度为O(1)。参考：

 

3.    选择排序：

思想：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后每次从剩余未排序元素中继续寻找最小（大）元素放到已排序序列的末尾。以此类推，直到所有元素均排序完毕

时间复杂度：最坏:O(n2) 最好: O(n2) 平均:O(n2)    O(1)

稳定性：不稳定 例如数组 2 2 1 3 第一次选择的时候把第一个2与1交换使得两个2的相对次序发生了改变。

 

4.    堆排序  

思想：堆排序是利用堆的性质进行的一种选择排序，先将排序元素构建一个最大堆,每次堆中取出最大的元素并调整堆。将该取出的最大元素放到已排好序的序列(堆顶有序区)前面。这种方法相对选择排序，时间复杂度更低，效率更高。

时间复杂度：最坏:O(nlog2n) 最好: O(nlog2n) 平均: O(nlog2n)

空间复杂度：O(1)

稳定性：不稳定 例如 5 10 15 10。 如果堆顶5先输出，则第三层的10(最后一个10)的跑到堆顶，然后堆稳定，继续输出堆顶，则刚才那个10跑到前面了，所以两个10排序前后的次序发生改变

 

5.    快速排序：

思想：【冒泡+二分+递归分治】，首先选择一个基准元素,根据基准元素将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。基准元素的选择对快速排序的性能影响很大，所有一般会想打乱排序数组选择第一个元素或则随机地从后面选择一个元素替换第一个元素作为基准元素。

时间复杂度：最坏:O(n2) 最好: O(nlogn) 平均: O(nlogn),O(nlogn)用于方法栈

稳定性：不稳定 快排会将大于等于基准元素的关键词放在基准元素右边，加入数组 1 2 2 3 4 5 选择第二个2 作为基准元素，那么排序后 第一个2跑到了后面，相对位置发生变化。

①随机化快速排序：若输入本身已被排序，那么对于快排来说就糟了Θ(n2)。那么如何避免这样的情况？一种方法时随机排列序列中的元素；另一种方法时随机地选择主元（pivot）。本方法只需在选取主元时加入随机因素即可。好处是：其运行时间不依赖于输入序列的顺序。 Θ(nlgn)。O(lgn)

srand(time(0));

inti=random()%(high-low)+low;

swap(a[i],a[low]);

(运行时间不依赖于输入，在虚拟内存的缓存中性能也很好)

②【快排对有序表比对无序表慢，为解决这个问题，同时提高快排的平均性能，采用三值取中规则——a[left],a[middle],a[right]三者中取中值作为支点元素，置换到表左端】

平均而言，快速排序是基于关键字比较的内部排序算法中速度最快者；但是由于快速排序采用的是递归的方法，因此当序列的长度比较大时，对系统栈占用会比较多。快速算法尤其适用于随机序列的排序

 

顺序统计找到第K小的元素/中位数

随机选择法（利用快排，比较第中间小的元素，确定在哪边找）Θ(n)（最坏Θ(n2)。）

最坏线性选择算法：保证每次划分两边的子数组都比较平衡，最坏情况下也能达到O(n)。

1）将输入数组的n个元素划分为n/5组，每组5个元素，且至多只有一个组有剩下的n%5个元素组成  2）首先对每组中的元素（5个）进行插入排序，然后从排序后的序列中选择出中位数  3）对第2步中找出的n/5个中位数，递归调用SELECT以找出其中位数x。（如果有偶数个中位数取较小的中位数）4）调用PARTITION过程，按照中位数x对输入数组进行划分。确定中位数x的位置k。5）如果i=k，则返回x。否则，如果i，则在低区间递归调用SELECT以找出第i小的元素，若干i>k，则在高区找第(i-k)个最小元素。

 

6.    计数排序：对一定范围内的整数排序时 Ο(n+k)（k是整数的范围，当O(k)>O(nlog(n))的时候其效率低于基于比较的排序），快于任何比较排序算法。牺牲空间换取时间。

7.    桶/箱排序(把元素映射到若干个桶中，先对桶中元素排序，再按次序排列各桶元素。桶内可采用别的排序方法) 桶越多，速度越快，但占内存越多。    

8.    基数排序：

思想：通过“分配”和“收集”过程来实现排序，首先根据数字的个位的数将数字放入0-9号桶中，然后将所有桶中所盛数据按照桶号由小到大，桶中由顶至底依次重新收集串起来，得到新的元素序列。然后递归对十位、百位这些高位采用同样的方式分配收集，直到没各位都完成分配收集得到一个有序的元素序列。

（类似于桶排序）将待排数据中的每组关键字依次进行桶分配，按个十百… 总是需要10个桶  【借助多关键字排序思想对单逻辑关键字进行排序的方法】

时间复杂度：最坏:O(d(r+n)) 最好:O(d(r+n)) 平均: O(d(r+n))

空间复杂度：O(dr+n)     n个记录，d个关键码，关键码的取值范围为r

稳定性：稳定 基数排序基于分别排序，分别收集，所以其是稳定的排序算法。

基数排序的性能比桶排序要略差，每次需要的桶的数量并不多，几乎不需要任何“比较”操作，而桶排序在桶相对较少的情况下，桶内多个数据必须进行基于比较操作的排序。因此，在实际应用中，基数排序的应用范围更加广泛。

 

9.        冒泡排序：相邻两个交换，及时终止。

思想：对待排序元素的关键字从后往前进行多遍扫描，遇到相邻两个关键字次序与排序规则不符时，就将这两个元素进行交换。这样关键字较小的那个元素就像一个泡泡一样，从最后面冒到最前面来。

时间复杂度：最坏：O(n2) 最好: O(n) 平均:O(n2)  空间复杂度：O(1)

稳定性：稳定，相邻的关键字两两比较，如果相等则不交换。所以排序前后的相等数字相对位置不变。

 

非比较排序[线性排序]：基数，计数，桶排序

非稳定排序：希尔，选择，堆，快排

 

其他：Bit排序算法，TopN算法，

 

参考：http://blog.csdn.net/hitxueliang/article/details/52077890

 http://www.cnblogs.com/jaylon/p/5735431.html