Matlab学习笔记 绘图函数详解
5.1 二维平面图形
5.1.1 基本图形函数
plot 是绘制二维图形的最基本函数,它是针对向量或矩阵的列来绘制曲线的。也就是
说,使用plot 函数之前,必须首先定义好曲线上每一点的x 及y 坐标,常用格式为:
(1)plot(x) 当x 为一向量时,以x 元素的值为纵坐标,x 的序号为横坐标值绘制
曲线。当x 为一实矩阵时,则以其序号为横坐标,按列绘制每列元素值相对于其序号的曲
线,
当x 为m× n 矩阵时,就由n 条曲线。
(2)plot(x,y) 以x 元素为横坐标值,y 元素为纵坐标值绘制曲线。
(3)plot(x,y1,x,y2,…) 以公共的x 元素为横坐标值,以y1,y2,… 元素为纵坐标值绘
制多条曲线。
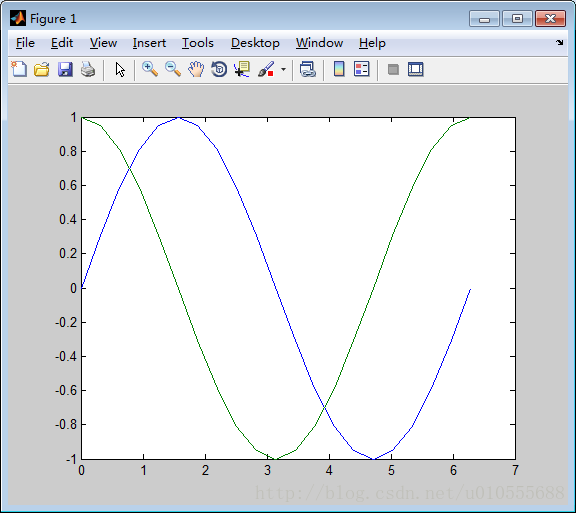
例5.1.1 画出一条正弦曲线和一条余弦曲线。
>> x=0:pi/10:2*pi;
>> y1=sin(x);
>> y2=cos(x);
>> plot(x,y1,x,y2)
在绘制曲线图形时,常常采用多种颜色或线型来区分不同的数据组,MATLAB 软件专门提供了这方面的参数选项(见表5.1.1),我们只要在每个坐标后加上相关字符串,就可实现它们的功能。
| 色彩字符颜色 | 线型字符线型格式 | 标记符号数据点形式 | 标记符号数据点形式 |
| y 黄 | - 实线 | . 点 | < 小于号 |
| m 品红 | : 点线 | o 圆 | s 正方形 |
| c 青 | -. 点划线 | x 叉号 | d 菱形 |
| r 红 | - - 虚线 | + 加号 | h 六角星 |
| g 绿 | v 向下三角形 | * 星号 | p 五角星 |
| b 蓝 | ^ 向上三角形 | > 大于号 | |
| w 白 | k 黑 |
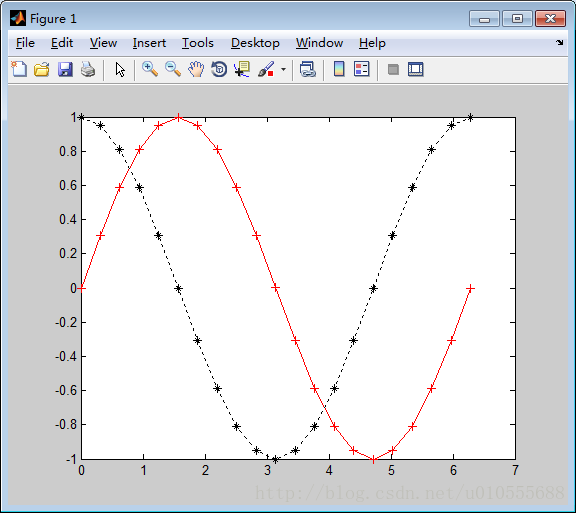
例如,在上例中输入
>> plot(x,y1,'r+-',x,y2,'k*:')则得图5.1.2如下
MATLAB 软件为用户提供了一些特殊的图形函数,用于修饰已经绘制好的图形,见 表5.1.2 图形修饰函数表。
| grid on (/off) | 给当前图形标记添加(取消)网络 |
| xlable(‘string’) | 标记横坐标 |
| ylabel(‘string’) | 标记纵坐标 |
| title(‘string’) | 给图形添加标题 |
| text(x,y,’string’) | 在图形的任意位置增加说明性文本信息 |
| gtext(‘string’) | 利用鼠标添加说明性文本信息 |
| axis([xmin xmax ymin ymax]) | 设置坐标轴的最小最大值 |
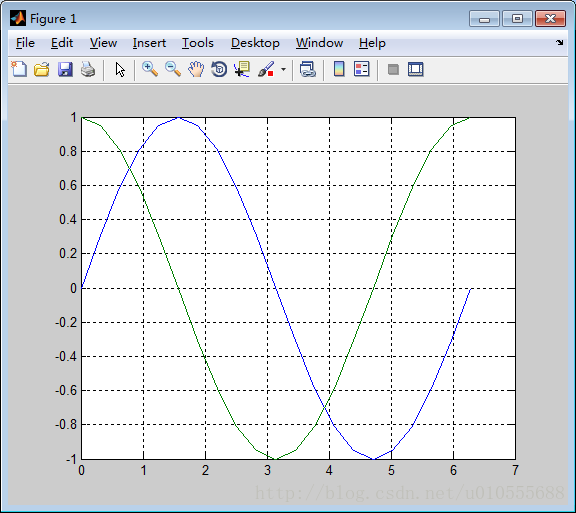
例5.1.2 给例5.1.1 的图形中加入网络和标记。(见图5.1.3 和5.1.4)
>> x=0:pi/10:2*pi;
>> y1=sin(x);
>> y2=cos(x);
>> plot(x,y1,x,y2)
>> grid on
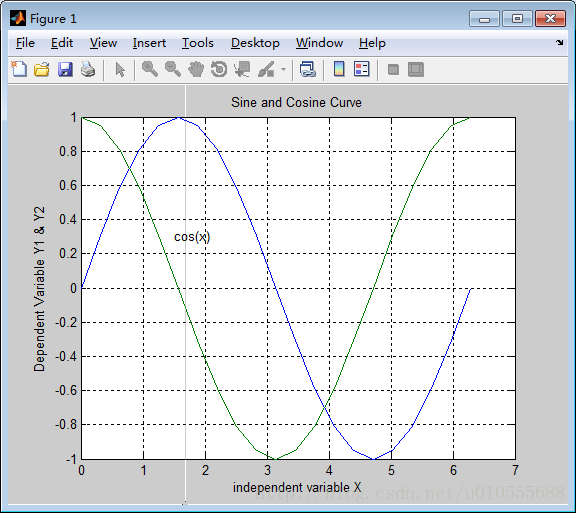
>> xlabel('independent variable X')
>> ylabel('Dependent Variable Y1 & Y2')
>> title('Sine and Cosine Curve')
>> text(1.5,0.3,'cos(x)')
>> gtext('sin(x)')
>> axis([0 2*pi -0.9 0.9])图5.1.3使用了图形修饰的plot 函数绘制的正弦曲线
在一般默认的情况下,MATLAB 每次使用plot 函数进行图形绘制,将重新产生一个图形窗口。但有时希望后续的图形能够和前面所绘制的图形进行比较。一般来说有两种方法:一是采用hold on(/off)命令,将新产生的图形曲线叠加到已有的图形上;二是采用subplot(m,n,k)函数,将图形窗口分隔成n m× 个子图,并选择第k 个子图作为当前图形,然后在同一个视图窗口中画出多个小图形。
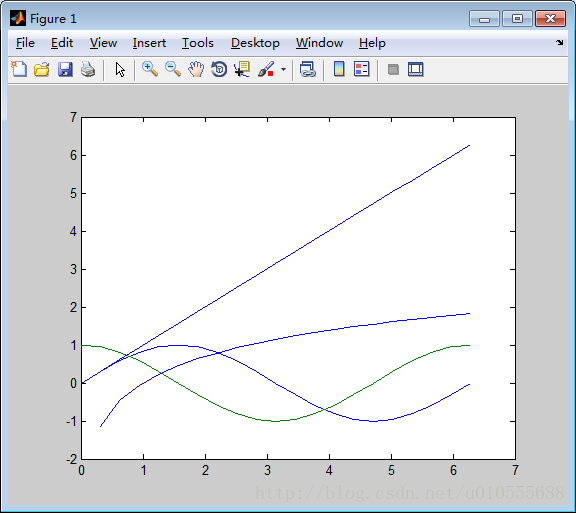
例5.1.3 在同一窗口中绘制线段。(见图5.1.5)>> x=0:pi/10:2*pi;
>> y1=sin(x);
>> y2=cos(x);
>> y3=x;
>> y4=log(x);
>> plot(x,y1,x,y2)
>> hold on
>> plot(x,y3)
>> plot(x,y4)
>> hold off图5.1.5 图形的比较显示(曲线叠加方法)
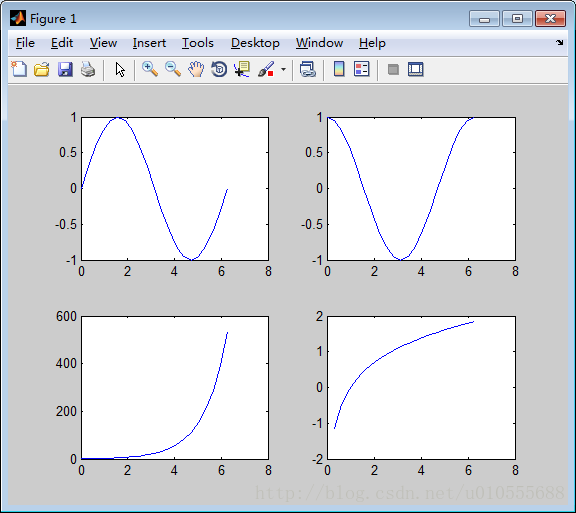
>> x=0:pi/10:2*pi;
>> y1=sin(x);
>> y2=cos(x);
>> y3=exp(x);
>> y4=log(x);
>> subplot(2,2,1);
>> plot(x,y1);
>> subplot(2,2,2);
>> plot(x,y2);
>> subplot(2,2,3);
>> plot(x,y3);
>> subplot(2,2,4);
>> plot(x,y4);[说明] (1)子窗口的序号按行由上往下,按列从左向右编号。
图5.1.6 图形的比较显示(图形窗口分割方法)
5.2 三维立体图形
5.2.1 三维曲线图
与二维图形相对应,MATLAB 提供了plot3 函数,可以在三维空间中绘制三维曲线,它的格式类似于plot,不过多了z 方向的数据。plot3 的调用格式为:
plot3(x1,y1,z1,x2,y2,z2,...),其中x1,y1,z1,x2,y2,z2,…等分别为维数相同的向量,分别存储着曲线的三个坐标值,该函数的使用方式和plot 类似,也可以采用多种的颜色或线型(见表5.1.1)来区分不同的数据组,只需在每组变量后面加上相关字符串即可实现该功能。
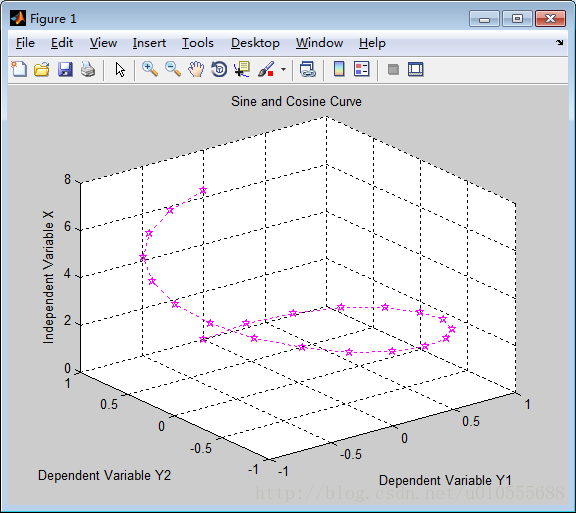
例5.2.1 绘制方程 x = t;y = sin(t);z = cos(t) 在t = [0,2*pi]上的空间方程。(见图5.2.1)
>> clf
>> x=0:pi/10:2*pi;
>> y1=sin(x);
>> y2=cos(x);
>> plot3(y1,y2,x,'m:p')
>> grid on
>> xlabel('Dependent Variable Y1')
>> ylabel('Dependent Variable Y2')
>> zlabel('Independent Variable X')
>> title('Sine and Cosine Curve')5.2.2 三维曲面图
如果要画一个三维的曲面,可以使用mesh(X,Y,Z)或surf(X,Y,Z)函数来实现。 mesh 函数为数据点绘制网格线,图形中的每一个已知点和其附近的点用直线连接。surf 函数和mesh 的用法类似,但它可以画出着色表面图,图形中的每一个已知点与其相邻点以 平面连接。 为方便测试立体绘图,MATLAB 提供了一个peaks 函数,它可以产生一个的高 斯分布矩阵,其生成方程是
N N × z=3*(1-x).^2.*exp(-(x.^2)-(y+1).^2)-10*(x/5-x.^3-y.^5).*exp(-x.^2-y.^2)-1/3*ex p(-(x+1).^2-y.^2)
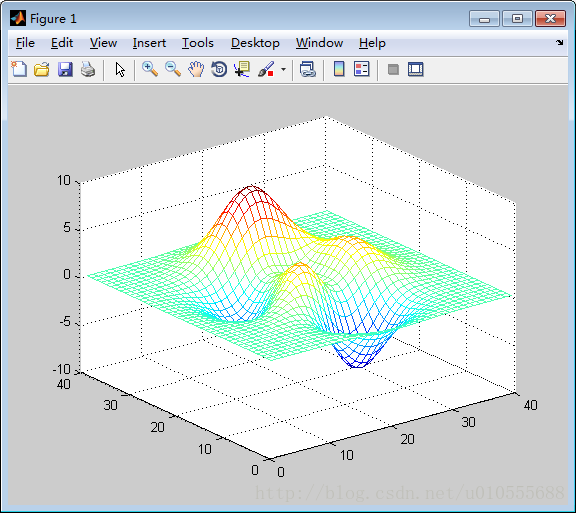
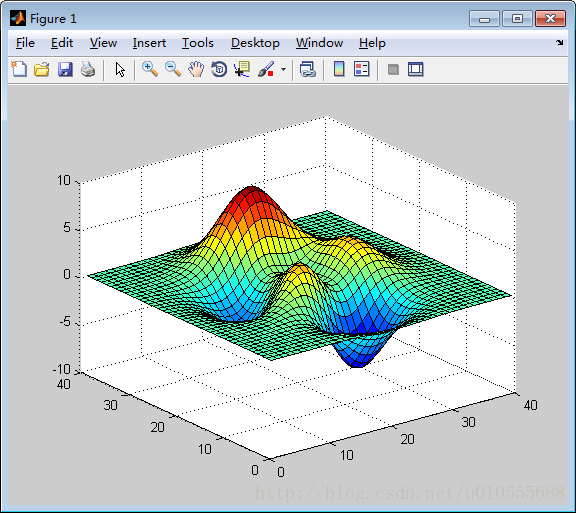
对应的图形是一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点。下面使用peaks 函数来比较一下mesh 和surf 的区别。
例5.2.2 分别用mesh 函数和surf 函数绘制高斯矩阵的曲面。>> z=peaks(40);
>> mesh(z);
>> surf(z);在曲面绘图中,另一个常用的函数是meshgrid 函数,其一般引用格式是:[X, Y]=meshgrid (x, y)。其中x 和y 是向量,通过meshgrid 函数就可将x 和y 指定的区域转换成为矩阵X 和Y。这样我们在绘图时就可以先用meshgrid 函数产生在x-y 平面上的二维的网格数据,再以一组z 轴的数据对应到这个二维的网格,即可画出三维的曲面。
sin((x^2+y^2)^(1/2))
z = --------------------- 在x∈[-7.5,7.5];y∈[-7.5,7.5] 的图形。
(x^2+y^2)^(1/2)
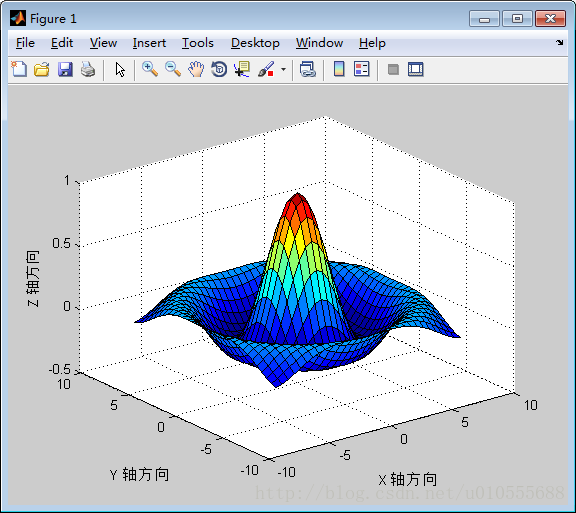
>> x=-7.5:0.5:7.5;y=x;
>> [X,Y]=meshgrid(x,y);
>> R=sqrt(X.^2+Y.^2)+eps;
>> Z=sin(R)./R;
>> surf(X,Y,Z)
>> xlabel('X 轴方向')
>> ylabel('Y 轴方向')
>> zlabel('Z 轴方向')(见图5.2.4)
图5.2.4
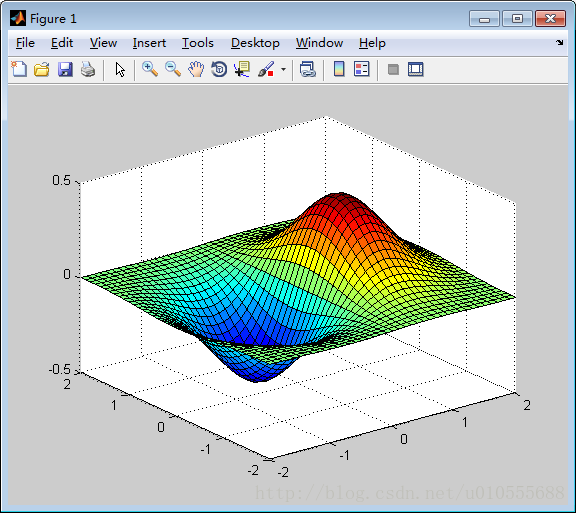
例5.2.4 绘制由方程形成的立体图。(见图5.2.5) z=x*exp(_(x^2+y^2) )
>> clear
>> x=-2:0.1:2;y=x;
>> [X,Y]=meshgrid(x,y);
>> Z=X.*exp(-X.^2-Y.^2);
>> surf(X,Y,Z)5.2.3 观察点
MTALAB 允许用户设置观察点,其指令是: view(azimuth,elevation)
其中方位角azimuth 是观察点和坐标原点连线在x-y 平面的投影和y 轴负方向的夹角,仰 角
elevation 是观察点与坐标原点的连线和x-y 平面的夹角。对于这两个角度,三维图形的默认值分别是-37.5 和30,二维图形的默认值是0 和90。
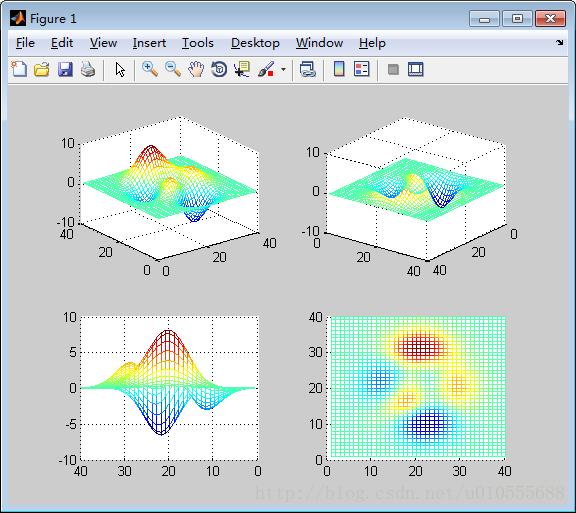
例5.2.5 从不同的角度观察高斯矩阵的曲面。
>> z=peaks(40);
>> subplot(2,2,1);
>> mesh(z);
>> subplot(2,2,2);
>> mesh(z);
>> view(-37.5,-30);
>> subplot(2,2,3);
>> mesh(z);
>> view(180,0);
>> subplot(2,2,4);
>> mesh(z);
>> view(0,90);除了plot 绘图函数以外,在有些场合对绘制的曲线会有一些特殊要求,这就要其他函 数来实现,常用的几种函数如下(见表5.3.1)
| loglog | 使用对数坐标系绘图 |
| semilogx | 横坐标为对数坐标轴,纵坐标为线性坐标轴 |
| semilogy | 横坐标为线性坐标轴,纵坐标为对数坐标轴 |
| polar | 绘制极坐标图 |
| fill | 绘制实心图 |
| bar | 绘制直方图 |
| pie | 绘制饼图 |
| area | 绘制面积图 |
| quiver | 绘制向量场图 |
| stairs | 绘制阶梯图 |
| sterm | 绘制火柴杆图 |
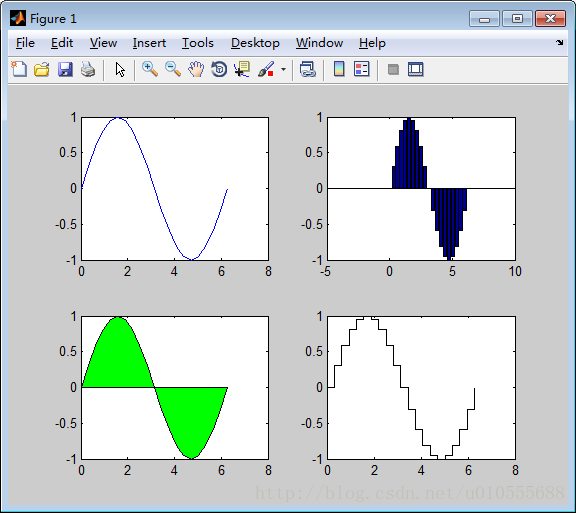
>> x=0:pi/10:2*pi;
>> y1=sin(x);
>> subplot(2,2,1);
>> plot(x,y1);
>> subplot(2,2,2);
>> bar(x,y1);
>> subplot(2,2,3);
>> fill(x,y1,'g');
>> subplot(2,2,4);
>> stairs(x,y1,'k');5.3.1 直方图
函数bar(x)可以绘制直方图,这对统计或者数据采集非常直观实用。它共有四种形式:bar,bar3,barh 和bar3h,其中bar 和bar3 分别用来绘制二维和三维竖直方图,barh 和bar3h 分别用来绘制二维和三维水平直方图,调用格式是:
bar(x,y) 。其中x 必须单调递增或递减,y 为n m× 矩阵,可视化结果为m 组,每组n 个垂直柱,也就是把y 的行画在一起,同一列的数据用相同的颜色表示;
bar(x,y,width) (或bar(y,width))指定每个直方条的宽度,如width>1,则直方条会重叠,默认值为width=0.8;
bar(…,’grouped’) 使同一组直方条紧紧靠在一起;bar(…,’stack’) 把同一组数据描述在一个直方条上。
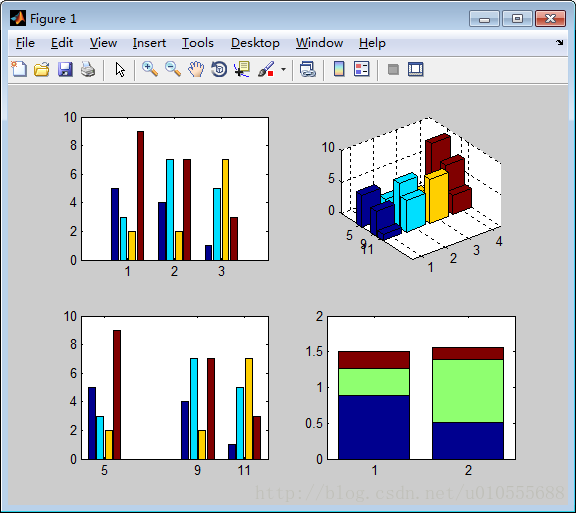
>> y=[5 3 2 9;4 7 2 7;1 5 7 3];
>> subplot(2,2,1),bar(y)
>> x=[5 9 11];
>> subplot(2,2,2),bar3(x,y)
>> subplot(2,2,3),bar(x,y,'grouped')
>> subplot(2,2,4),bar(rand(2,3),.75,'stack')函数area 用来绘制面积图,面积图在plot 的基础上填充x 轴和曲线之间的面积,该图用于查看某个数在该列所有数的总和中所占的比例。
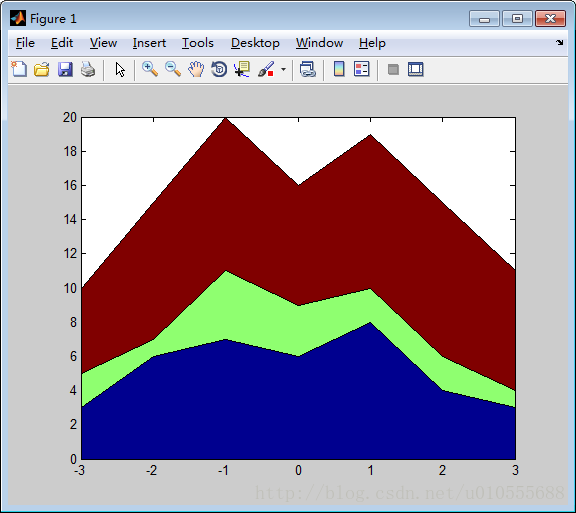
例5.3.3
>> x=-3:3;
>> y=[3 2 5;6 1 8;7 4 9;6 3 7;8 2 9;4 2 9;3 1 7];
>> area(x,y)函数pie 用来绘制饼图,它可以形象地表示出向量中各元素所占比例。其调用格式是:
pie(x) x 中的元素通过x/sum(x)进行归一化,以确定饼图中的份额;
pie(x,explode) 向量explode 和x 元素数相同,用来指出需要分开的饼片,explode 中不为零的部分会被分开。
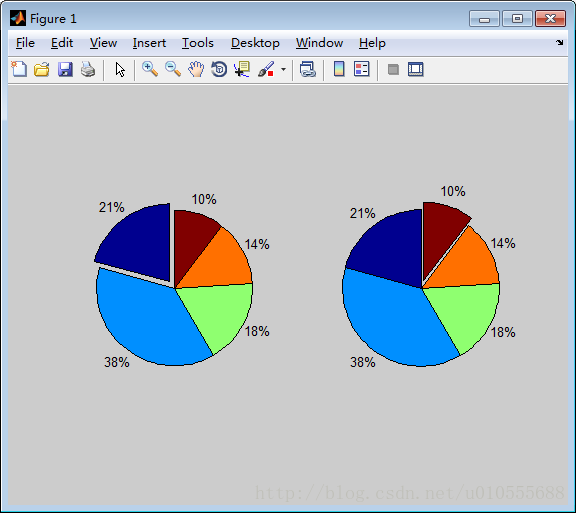
>> x=[32 58 27 21 16];
>> explode0=[1 0 0 0 0];
>> subplot(1,2,1)
>> pie(x,explode0)
>> explode1=[0 0 0 0 1];
>> subplot(1,2,2)
>> pie(x,explode1)图5.3.4
Semilogx,semilogy,loglo,polar(theta,rho)的使用方法和plot 完全类似,不同的只是绘制到不同的图形坐标上。函数semilogx 绘制x 轴为对数标度的图形,在半对数坐标系中绘图;
函数semilogy 绘制y 轴为对数标度的图形;函数loglog 绘制两个轴都为对数间隔的图形;
函数polar(theta,rho)绘制极坐标图形,其中theta 为相角,rho 为其对应的半径。
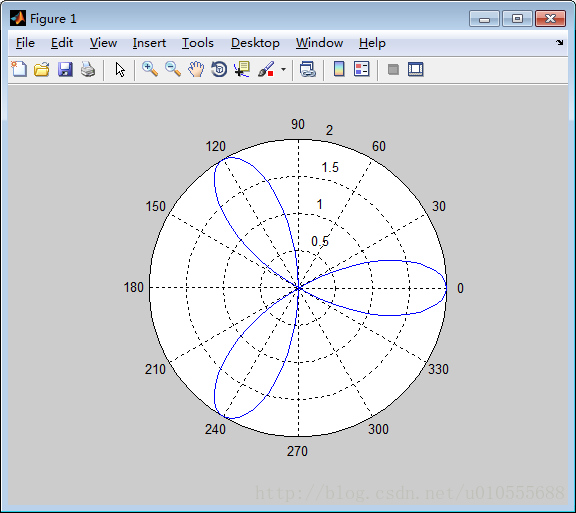
例5.3.5 绘制ρ=acos(3θ),a=2 的图形。(见图5.3.5)
>> theta=-pi:pi/80:pi;
>> polar(theta,2*cos(3*theta))MATLAB 软件提供了将表达式进行图形显示的功能。完成此功能需调用fplot 函数和 ezplot 函数。
函数fplot 用来绘制数学函数,其调用格式为: fplot(fun,lims)。 其中fun 就是所要绘制的函数,可以是定义函数的M 文件名,也可以是以x 为变量的可计 算字符串。例如’diric(x,10)’或’[sin(x),cos(x)]’,对于向量x 的每个元素,函数 fun(x)必须返 回一个行向量。如果fun 返回[f1(x),f2(x),f3(x)],输入[x1;x2],就会返回矩阵
f1(x1) f2(x1) f3(x1)
f1(x2) f2(x2) f3(x2)
lims=[XMIN XMAX YMIN YMAX]限定了x,y 轴上的绘图空间。
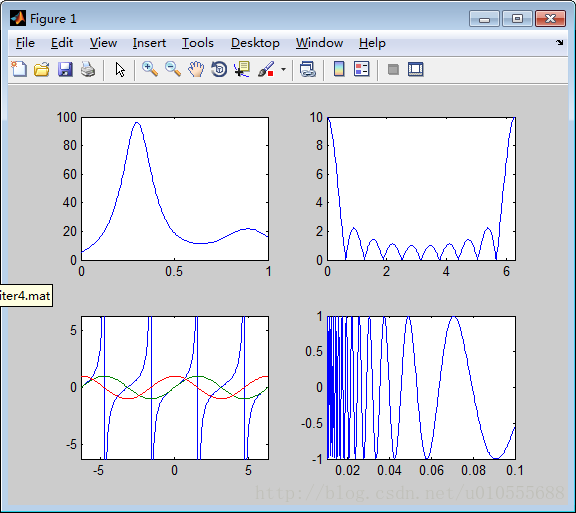
例5.4.1
>> subplot(2,2,1),fplot('humps',[0 1])
>> subplot(2,2,2),fplot('abs(exp(-j*x*(0:9))*ones(10,1))',[0 2*pi])
>> subplot(2,2,3),fplot('[tan(x),sin(x),cos(x)]',2*pi*[-1 1 -1 1])
>> subplot(2,2,4),fplot('sin(1./x)',[0.01 0.1],1e-3)ezplot 函数是简捷绘图指令之一,它无需数据准备,直接画出函数图形,基本调用格式为ezplot(f),其中f 是字符串或代表数学函数的符号表达式,只有一个符号变量,可以是x,缺省情况下x 轴的绘图区域为 [−2π,2π] ,但我们可以用ezplot(f,xmin,xmax)或ezplot(f,[xmin,xmax])来指定x 的范围。
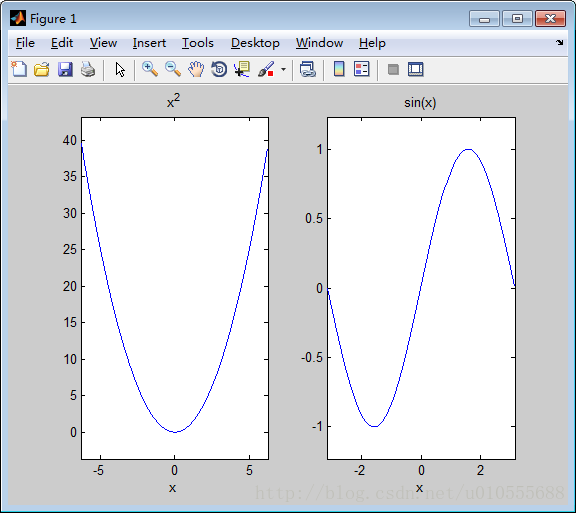
例5.4.2
>> y='x^2';
>> subplot(1,2,1)
>> ezplot(y)
>> subplot(1,2,2)
>> y='sin(x)';
>> ezplot(y,[-pi,pi])MATLAB 对数据是按列存储和计算的,运用plot(x)时,当x 为一个向量时,以其元 素为纵坐标,其序号为横坐标值绘制曲线。当x 为实矩阵时,则以其序号为横坐标,按列 绘 制每列元素相对于序号的曲线,当x 为n m× 矩阵时,就有n 条曲线。 如果x,y 是同维向量,plot(x,y)指令以x 元素为横坐标值,y 元素为纵坐标值绘制曲线。
如x 是向量,y 是有一维与x 元素数量相等的矩阵,则以x 为共同横坐标,按列绘制y 每列元素值,曲线数为y 的另一维的元素数。如果x,y 是同维矩阵,则以x,y 对应列元素为、纵坐标分别绘制曲线,数目等于矩阵的列数。
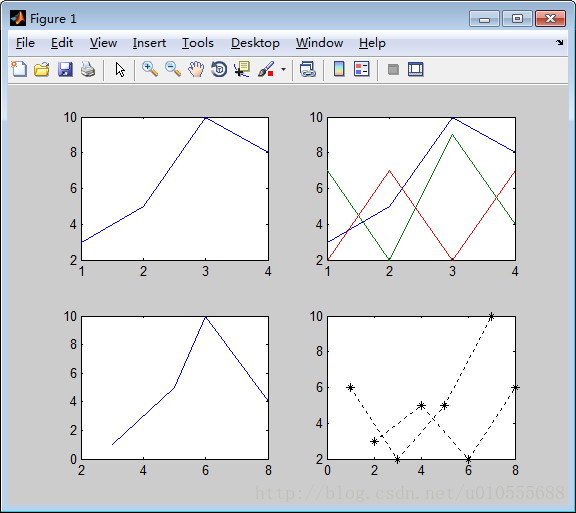
例5.5.1
>> x=[3 5 10 8];
>> subplot(2,2,1)
>> plot(x)
>> x=[3 5 10 8;7 2 9 4;2 7 2 7]';
>> subplot(2,2,2)
>> plot(x)
>> x=[3 5 6 8];
>> y=[1 5 10 4];
>> subplot(2,2,3)
>> plot(x,y)
>> x=[1 3 5 7;2 4 6 8]';
>> y=[6 2 5 10;3 5 2 6]';
>> subplot(2,2,4)
>> plot(x,y,'k:*')ginput 是一个比较特殊的图形指令,用作获取图上数据,例如指令 [x,y]=ginput(6) % 从图形上选取6 个点
此时,ginput 指令将把当前图形调入前台,同时光标变为十字叉,移动光标,使交叉点落 在 目标点上,单击鼠标,即可获得该点数据。
例5.5.2
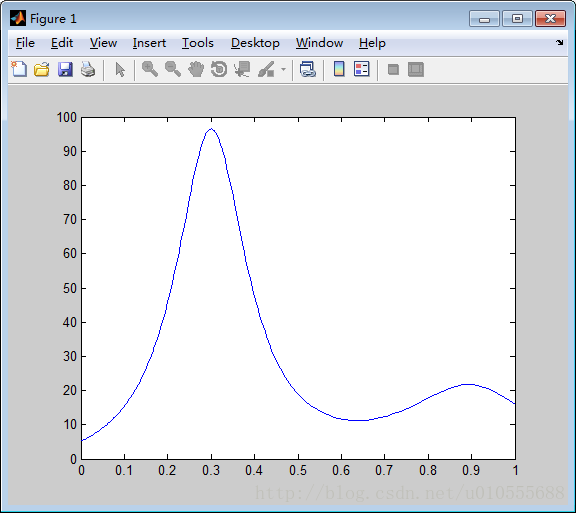
>> fplot('humps',[0 1])
>>[x,y]=ginput(6);x =
0.0449
0.1832
0.3007
0.3813
0.6417
0.8952
y =
7.4561
38.1579
96.3450
57.4561
10.9649
21.1988参考:http://jiangkeke.blog.hexun.com/37733622_d.html