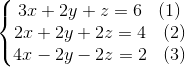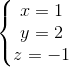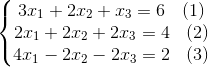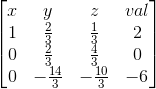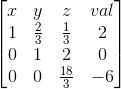线性代数 —— 高斯消元法

【概述】

高斯消元法主要用于求解线性方程组，也可以求矩阵的秩、矩阵的逆等，是一个重要的数学方法。

其时间复杂度主要与方程组个数、方程组未知数个数有关，一般来说，时间复杂度为 O(n^3)

【线性方程组】

线性方程组：有多个未知数，且每个未知数的次数均为一次，这样多个未知数所组成的方程组。

其形式为：

记为矩阵形式，有：

 

【高斯消元法】

高斯消元法的基本思想是：通过一系列的加减消元运算，直到得到类似 kx=b 的式子，然后逐一回代求解 x 向量

1.解方程组过程

以以下线性方程组为例

首先进行消元操作：

将 (1) 除以 3，把 x 的系数化为 1，得：

再令 (2)-2*(1)'、(3)-4*(1)'，将 (2)、(3) 的 x 消去，得：

将令 (2)' 除以 2/3，将 y 系数化为 1，得：

再令 (3)'-(-14/3)*(2)''，将 (3)' 的 y 消去，得：

由 (3)'' 可得：

最后进行回代操作：

将  带回 (2)'' 可得：

将 、 带回 (1)' 可得：

即结果为：

2.矩阵运算消元过程

同样以以下线性方程组为例

将其记为矩阵形式，有：

消去 x，有：

消去 y，有：

回代得解：

3.解的判断

无解：当消元完毕后，发现有一行系数都为 0，但是常数项不为 0，此时无解

例如：

多解：当消元完毕后，发现有多行系数、常数项均为 0，此时多解，有几行为全为 0，就有几个自由元，即变量的值可以任取，有无数种情况可以满足给出的方程组

例如：，此时自由元个数为 2

【实现】

1.线性方程组整数类型解

int a[N][N];//增广矩阵
int x[N];//解集
bool freeX[N];//标记是否为自由变元
int GCD(int a,int b){
    return !b?a:GCD(b,a%b);
}
int LCM(int a,int b){
    return a/GCD(a,b)*b;
}
int Gauss(int equ,int var){//返回自由变元个数
    /*初始化*/
    for(int i=0;i<=var;i++){
        x[i]=0;
        freeX[i]=true;
    }

    /*转换为阶梯阵*/
    int col=0;//当前处理的列
    int row;//当前处理的行
    for(row=0;rowabs(a[maxRow][col]))
                maxRow=i;
        }
        if(maxRow!=row){//与第row行交换
            for(int j=row;j=0;i--){//计算解集
        int temp=a[i][var];
        for(int j=i+1;j0){//有无穷多解
            printf("有无穷多解，自由变元个数为%d\n",freeNum);
            for(int i=0;i

2.线性方程组浮点类型解

double a[N][N];//增广矩阵
double x[N];//解集
bool freeX[N];//标记是否为自由变元

int Gauss(int equ,int var){//返回自由变元个数
    /*初始化*/
    for(int i=0;i<=var;i++){
        x[i]=0;
        freeX[i]=true;
    }

    /*转换为阶梯阵*/
    int col=0;//当前处理的列
    int row;//当前处理的行
    for(row=0;rowabs(a[maxRow][col]))
                maxRow=i;
        }
        if(maxRow!=row){//与第row行交换
            for(int j=row;j1e6){
                double temp=a[i][col]/a[k][col];
                for(int j=col;j1e6)
            return -1;

    //无穷解: 在var*(var+1)的增广阵中出现(0,0,...,0)这样的行
    int temp=var-row;//自由变元有var-row个
    if(row=0;i--){//计算解集
        double temp=a[i][var];
        for(int j=i+1;j

3.模线性方程组

在解模线性方程组组时，当有唯一解时，需要对每个方程的唯一解不断的循环取模判断，直到找出能整除的为止

int a[N][N];//增广矩阵
int x[N];//解集
bool freeX[N];//标记是否为自由变元
int GCD(int a,int b){
    return !b?a:GCD(b,a%b);
}
int LCM(int a,int b){
    return a/GCD(a,b)*b;
}
int Gauss(int equ,int var){//返回自由变元个数
    /*初始化*/
    for(int i=0;i<=var;i++){
        x[i]=0;
        freeX[i]=true;
    }

    /*转换为阶梯阵*/
    int col=0;//当前处理的列
    int row;//当前处理的行
    for(row=0;rowabs(a[maxRow][col]))
                maxRow=i;
        }
        if(maxRow!=row){//与第row行交换
            for(int j=row;j=0;i--){//计算解集
        int temp=a[i][var];
        for(int j=i+1;j

4.异或方程组 

异或方程组是指形如  的方程组

对于 k=1...n，找到一个 a[i][k] 不为 0 的行 i，把它与第 k 行交换，用第 k 行去异或下面所有 a[i][j] 不为 0 的行 i，消去它们的第 k 个系数，这样就将原矩阵化成了上三角矩阵

由于最后一行只有一个未知数，这个未知数就已经求出来了，然后用它跟上面所有含有这个未知数的方程异或，以此类推即可以自下而上求出所有未知数。

要注意的是，对于开关问题，a[i][j]=1 表示第 i 个开关受第 j 个开关影响

int a[N][N];//增广矩阵
int x[N];//解集
int freeX[N];//自由变元
int Gauss(int equ,int var){//返回自由变元个数
    /*初始化*/
    for(int i=0;i<=var;i++){
        x[i]=0;
        freeX[i]=0;
    }

    /*转换为阶梯阵*/
    int col=0;//当前处理的列
    int num=0;//自由变元的序号
    int row;//当前处理的行
    for(row=0;rowabs(a[maxRow][col]))
                maxRow=i;
        }
        if(maxRow!=row){//与第row行交换
            for(int j=row;j=0;i--){//计算解集
        x[i]=a[i][var];
        for(int j=i+1;j=0;k--){//没有自由元的最下面一行
            int index=0;
            for(index=k;k

【例题】

• Widget Factor（POJ-2947）(模线性方程组)：点击这里
• SETI（POJ-2065）(模线性方程组)：点击这里
• EXTENDED LIGHTS OUT（POJ-1222）(异或方程组)：点击这里
• 开关问题（POJ-1830）(异或方程组自由元个数)：点击这里
• The Water Bowls（POJ-3185）(异或方程组统计有解情况下1最少的个数)：点击这里