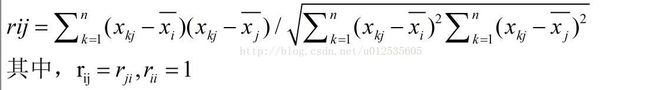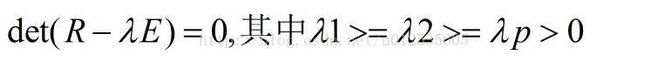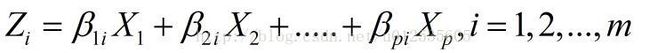数据降维--------主成分分析（PCA）算法原理和实现学习笔记

1 主成分分析背景

'''PCA计算步骤（思想是把数据投影到方向向量使数据集的特征向量到方向向量的垂线长度最短）
1.去平均
2.计算协方差矩阵
3.计算协方差矩阵的特征向量和特征值
4.将特征值从小到大排列
5.保留最上面的n个特征向量
6.将数据转换到上述n个特征向量构建新的空间
'''

备注：降维过的方向向量就是新的数据集、特征向量就是数据集维度个数，通过特征向量个数限制降维的维数

在大数据集上进行复杂的分析和挖掘需要很长的时间，数据降维产生更小但保持数据完整性的新数据集，在降维后的数据集上进行分析和挖掘将更有效率

数据降维的意义：

1）降低无效、错误的数据对建模的影响，提高建模的准确性

2）少量且具有代表性的数据将大幅缩减数据挖掘所需要的时间

3）降低存储数据的成本

2主成分分析原理

主成分分析（Principal Component Analysis，PCA）：主成分分析是一种用于连续属性的数据降维方法，它构造了原始数据的一个正交变换，新空间的基地去除了原始空间基底下数据的相关性，只需要使用少数新变量就能够解释原始数据中大部分变量。在应用中通常是选出比原始变量个数少，能够解释大部分数据中的变量的几个新变量，即所谓的主成分，来代替原始变量进行建模。通过线性变化，将原始数据集变化为一组各维度线性无关的表示

例如一个数据维度如下

姓名	年龄	手机号	性别	性别标签	浏览	访问
xx	yy	zz	M	男	12	3
22	33	44	F	女	45	5

性别和性别标签若去掉其中一个并不影响数据的完整性

3主成分分析计算步骤

1）设原始变量X1，X2...Xp的n次观测数据矩阵为：

 

2）将数据矩阵按列进行中心标准化，为了方便将标准化后的数据矩阵仍然记为X

3)求相关系数矩阵R，rij的定义如下

4）求R的特征方程

)

5)确定主成分的个数

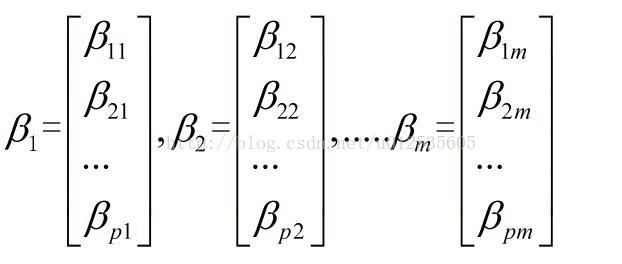
6）计算m个相应的单位特征向量：

7）计算主成分

4 主成分分析应用

Python代码实现

———————————————————————————————————————————————————————import pandas as pd
from sklearn.linear_model import  LogisticRegression  as LR
from sklearn.decomposition  import PCA
data=pd.read_excel('categ_lvl3.xlsx')
select_var = ~data.columns.isin(["CATEG_LVL3_ID","CATEG_LVL3_NAME","CATEG_LVL1_ID","FLAG","PROB","FLAG_PRE"])
pre_data = data.ix[:, select_var]
pre_Y=data.FLAG.values
pca=PCA()
fit_data=pca.fit(pre_data)
model_vec=pca.components_  #返回模型的各个特征向量
var_ratio=pca.explained_variance_ratio_  #返回各个成分各自的方差百分比（贡献率）

print var_ratio
#优化方法

#pca_new.inverse_transform(low_d)#恢复原数据
estimator=PCA(n_components=3)
X_pca=estimator.fit_transform(pre_data)
print estimator.n_components
print estimator.explained_variance_ratio_
lr=LR()
lr.fit(X_pca,pre_Y)
print ('利用PCA降维后的数据得到的准确率:%s' % lr.score(X_pca,pre_Y))
lr1=LR()
lr1=lr1.fit(pre_data,pre_Y)
print ('未做降维得到的准确率:%s' % lr1.score(pre_data,pre_Y))
 

————————————————————————————————————————————————————

输出结果

————————————————————————————————————————————————————

>>> runfile('D:/Python/PCA.py', wdir='D:/Python')
[  9.70006256e-01   2.30376474e-02   5.00288142e-03   1.43720555e-03
   2.24913835e-04   1.53242060e-04   8.26331017e-05   3.03412572e-05
   1.41397603e-05   5.61639854e-06   1.90652038e-06   1.09702291e-06
   7.85569385e-07   6.53679927e-07   2.83414351e-07   1.73934450e-07
   1.08756968e-07   6.12746381e-08   3.33729063e-08   1.06064072e-08
   2.92826594e-09   2.24209695e-09   1.65247674e-09   1.27594269e-09
   1.05333673e-09   1.13539542e-10   7.35525941e-11   2.31510033e-11
   2.23194676e-11   1.69164862e-11   9.70553560e-12   1.85863997e-12
   1.61107550e-12   3.09137415e-13   2.09741813e-13   9.73050317e-14
   2.76837387e-14   1.79763523e-14   2.49077050e-16   7.37908376e-17
   4.71563324e-17   4.04849479e-17   1.75061435e-17   1.16350857e-17
   3.58091370e-18   2.54690677e-18   1.82368863e-18   1.58131605e-18
   1.15795426e-18   9.02905224e-19   4.58671469e-19   3.69813198e-19
   8.17727206e-20   7.23473191e-20   2.80392291e-20   1.11750601e-20
   2.32693783e-21   1.42270896e-22   5.40932102e-33   5.40932102e-33
   5.40932102e-33   5.40932094e-33]
3
[ 0.97000626  0.02303765  0.00500288]
利用PCA降维后的数据得到的准确率:0.885357548241
未做降维得到的准确率:0.862656072645

——————————————————————————————————————

原始数据由原来的62维降到了3维，同时这3维数据占原数据的99.8%以上的信息，