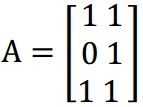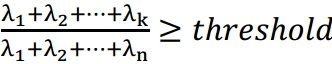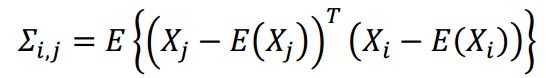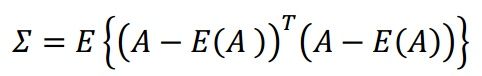SVD、PCA小结
本文不详细介绍SVD的物理意义以及数学上的严谨证明,而是详细介绍SVD的求解过程以及简单描述SVD与PCA 千丝万缕的联系。
假设有矩阵![]() 而且为满秩的,这里假设m>n,则有
而且为满秩的,这里假设m>n,则有![]() ,满秩矩阵又称非退化矩阵,具有非退化的奇异值。
,满秩矩阵又称非退化矩阵,具有非退化的奇异值。
奇异值分解是指将矩阵![]() 分解为
分解为![]() ,
,![]() 其中的每一个向量被成为左奇异向量,
其中的每一个向量被成为左奇异向量,![]() ,其中每一个列向量被称为右奇异向量,而
,其中每一个列向量被称为右奇异向量,而![]() 为对角阵,其对角线元素即为奇异值。
为对角阵,其对角线元素即为奇异值。
SVD的几何意义这里不再细究,举个简单的例子:在文本中矩阵![]() 每行代表一个文档,每列代表一个特征,对
每行代表一个文档,每列代表一个特征,对![]() 进行奇异值分解之后,大家大致可以将矩阵
进行奇异值分解之后,大家大致可以将矩阵![]() 看作文档到主题的映射矩阵,而
看作文档到主题的映射矩阵,而![]() 看作主题到单词的映射矩阵,其中主题的重要程度可由矩阵
看作主题到单词的映射矩阵,其中主题的重要程度可由矩阵![]() 间接指出。
间接指出。
SVD的求解过程,对矩阵![]() 进行奇异值分解,其中矩阵
进行奇异值分解,其中矩阵![]() 为满秩矩阵:
为满秩矩阵:
解:
求注意:使用![]() 只能求出前n个左奇异向量
只能求出前n个左奇异向量![]() ,而后m-n个左奇异向量需要通过解方程的方式求得。
,而后m-n个左奇异向量需要通过解方程的方式求得。
下面证明![]() 与
与![]() 之间的关系:
之间的关系:
因为特征向量![]() 与
与![]() 之间满足正交约束。
之间满足正交约束。
所有的![]() 与
与![]() 全部求出以后,按照奇异值
全部求出以后,按照奇异值![]() 从大到小的顺序排序即可,而
从大到小的顺序排序即可,而![]() 中,第n+1到第m个顺序可以任意。
中,第n+1到第m个顺序可以任意。
在实际应用中,通常只需取![]() ,其中
,其中![]() 中为前K个最大的奇异值,而U与V中则为其对应的左右奇异值向量。
中为前K个最大的奇异值,而U与V中则为其对应的左右奇异值向量。
举例说明:(网上找的题目)
解法改成贴图啦,一个个的粘公式实在是太麻烦了~~
由于个人水平限制,对于SVD的解释就讲到这里啦,下面简单介绍一下PCA以及PCA与SVD之间的关系。^@^
主成分分析 Principal Components Analysis(PCA)
PCA是一种非监督方法,能够在没有输入信息的前提下,将特征映射到某一个空间中,而且保证在空间中,特征之间的方差能够达到最大化。
假设样本表示为向量![]() ,而将样本映射到空间中
,而将样本映射到空间中![]() 可以表示为,在空间
可以表示为,在空间![]() 中的方差则可以表示为
中的方差则可以表示为![]() ,其中
,其中![]() 为样本各个特征之间的协方差矩阵。
为样本各个特征之间的协方差矩阵。
由此,第一主成分即使得特征之间方差达到最大的那一空间,可表示为![]() ,为了保证最大值存在,我们约束
,为了保证最大值存在,我们约束![]() ,从而有
,从而有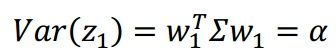 ,因为
,因为![]() ,所以左乘
,所以左乘![]() 后,有
后,有![]() 。由此可见,其实
。由此可见,其实![]() 是协方差矩阵的特征向量,而方差为其对应的特征值。
是协方差矩阵的特征向量,而方差为其对应的特征值。
为了使方差最大,我们选取最大的特征值![]() 对应的特征向量作为
对应的特征向量作为![]() ,如此可将原特征映射到空间
,如此可将原特征映射到空间![]() 中。由映射
中。由映射![]() 得到的值,即为由原特征组合而成的第一主成分。
得到的值,即为由原特征组合而成的第一主成分。
第二主成分空间与第一主成分正交,即满足![]() ,仔细分析后发现,
,仔细分析后发现,![]() 其实就是协方差矩阵
其实就是协方差矩阵![]() 第二大特征值所对应的特征向量(这里要知道,不同特征值之间的特征向量以及相同特征值之间的不同特征向量相互之间正交)。
第二大特征值所对应的特征向量(这里要知道,不同特征值之间的特征向量以及相同特征值之间的不同特征向量相互之间正交)。
举例说明,在文本中,我们用行表示文档,列表示特征,而空间映射正交基![]()
![]() ,从而可将文档用主成份表示,表示方法如下:
,从而可将文档用主成份表示,表示方法如下:![]() ,而实际中,我们可由主成份所对应的特征值来表示主成份在所有主成份中的重要程度,通常,我们可以通过公式
,而实际中,我们可由主成份所对应的特征值来表示主成份在所有主成份中的重要程度,通常,我们可以通过公式
好啦,简单介绍完PCA之后呢,就再回到主题,SVD与PCA之间有什么关系呢?
假设原文档进行SVD后,为
单单看样子和约束,SVD似乎可以直接用在PCA的求解中。实际上,解决PCA问题时,也都是 SVD去求解,这是为什么呢?
前面介绍过,求解SVD时,实际是对矩阵![]() 求解特征值与特征向量,而求解PCA时,实际是对协方差矩阵求解特征值与特征向量。矩阵中的每一列代表一个文档,即行为特征。
求解特征值与特征向量,而求解PCA时,实际是对协方差矩阵求解特征值与特征向量。矩阵中的每一列代表一个文档,即行为特征。
再看协方差矩阵的求法,已知样本为X,在这里即表现为矩阵![]() 的行向量,则
的行向量,则
矩阵表示即为
可见,矩阵![]() 与矩阵
与矩阵![]() 在求解过程中,差别主要在是否减去了矩阵
在求解过程中,差别主要在是否减去了矩阵![]() 的期望(减去期望,可以看作对整个矩阵进行平移,X,Y轴两个方向)。
的期望(减去期望,可以看作对整个矩阵进行平移,X,Y轴两个方向)。
当使用SVD进行PCA时呢,我们只需要抛出E(A)的影响就可以啦,怎么抛出呢?太简单啦,让E(A)=0就行喽。
这样子,就可以直接使用SVD的结果作为PCA的结果,而主成份即右奇异矩阵![]() ,而映射后的样本就是左奇异矩阵与奇异值的乘积即
,而映射后的样本就是左奇异矩阵与奇异值的乘积即![]() 。
。
所以啦,所以啦,使用SVD进行PCA的求解时呢,其实是用了假设的先验信息,所有样本的期望E(X)=0。
问题:
假设时,使用SVD对样本做PCA会有什么样的影响?
希望看到此博客的大神能够解惑。