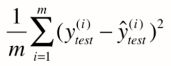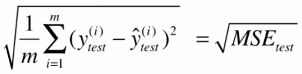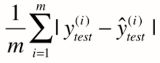机器学习基础算法梳理-1
目录
- 机器学习基础算法梳理
- 一、机器学习基本概念
- 1.1 监督学习(Supervised Learning)
- 1.2 无监督学习(Unsupervised Learning)
- 1.3 泛化能力(Generalization Ability)
- 1.4 过拟合(Overfitting)
- 1.5 欠拟合(Underfitting)
- 1.6 估计泛化能力(Bias-Variance Decomposition)
- 二、线性回归相关概念
- 2.1 线性回归原理(Linear Regression)
- 2.2 损失函数(Loss Function)
- 2.3 代价函数(评分函数 Score Function)
- 2.4 目标函数(target function)
- 2.5 优化方法
- 2.5.1 梯度下降法(Gradient Descent)
- 2.5.2 牛顿法(Newton's Method)
- 2.5.3 拟牛顿法(Quasi-Newton Methods)
- 2.6 线性回归的评估指标
- 2.6.1 均方误差MSE(Mean Squared Error)
- 2.6.2 均方根误差RMSE(Root Mean Squared Error)
- 2.6.3 平均绝对误差MAE(Mean Absolute Error)
- 三、Sitkit-learn 参数详解
机器学习基础算法梳理
一、机器学习基本概念
1.1 监督学习(Supervised Learning)
简述:通过学习一组给定标签输入与输出的数据,对其相应的输出做一个预测,称为监督学习
例子:小明目前有一批患者肠镜的影片,通过影片数据的学习来预测该病人是否患有结直肠。该问题有且只有两个回答 【有】 【没有】。 而我们学习的对象可以是患者肠镜颜色的深浅,患者年龄,影片上小肠粘膜光滑程度、肝区、横结肠是否有扁平息肉等特征进行判断。这里的特征均由我们主观意识给定。在给定数据与学习的样本的特征,此称为监督学习。
1.2 无监督学习(Unsupervised Learning)
简述:通过学习一组无标签的数据,来达到对同类数据相似的输出,称为无监督学习
例子:小明目前有一大批猫相片的数据,但是这批数据没有任何特征,也就是我们不能通过图片中猫的颜色、毛发、长短、光影、形状等等来进行判断。可以把其理解为这是一个黑盒测试,我们对数据的属性一无所知,只知道达到的结果是通过学习这批数据判断一张新的图片是否为期望的对象,此称为无监督学习。
1.3 泛化能力(Generalization Ability)
简述:指由某种方法学习到的模型对未知数据的预测能力
详解:这种评价是针对于训练集与测试集而言的,所以效果未必能泛化,模型的泛化指在对数据集之外的数据进行评估的能力。在此引申出两种泛化的常见问题与解决思路:过拟合与欠拟合,交叉验证
1.4 过拟合(Overfitting)
简述:模型对于训练集的数据过于敏感,也就是在训练的时候达到的正确率非常高,导致在测试集合与数据集之外的数据预测准确率低下的现象叫做过拟合
常见解决思路:正则化、交叉验证、dropout、扩大训练集、学习率衰减等等
1.5 欠拟合(Underfitting)
简述:模型对于训练集的数据不够敏感,无法通过现有的特征与数据给出准确的预测,导致预测结果偏低的现象叫做欠拟合。
常见解决思路:添加特征项、添加多项式特征、减少正则化参数等等。
1.6 估计泛化能力(Bias-Variance Decomposition)
通常我们在评估一个算的时候需要了解具体的 ”为什么“ 具有这样的性能,”偏差-方差分解“就是解释学习算法泛化性能的一种重要工具
此处不对公式进行过多推导,最终得到的泛化误差为:
E(f; D) = bias ^ 2(x) + var(x) + e ^ 2
等价于,泛化误差分解为偏差、方差与噪声之和。偏差度量的是算法的期望预测与真是结果的偏离程度,也就是算法本身的拟合能力;方差度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响;噪声则表达了再当前任务上任何学习算法所能达到的预期泛化的下界,即刻画了学习问题本身的难度。
二、线性回归相关概念
2.1 线性回归原理(Linear Regression)
简述:回归是基于已有的数据对新的数据进行预测,根据线性代数,我们定义线性方程组:
Xw = y,
在线性回归问题中,X为样本数据矩阵,y是期值向量。也就是说,对于线性回归的问题中,X与y是已知的,我们要解决的问题是取得最合适的一个向量W,使方程组中的能够尽量满足样本点的线性分布,之后就可以基于W对新的样本进行预测。
2.2 损失函数(Loss Function)
简述:用来量化预测分类标签的得分与真实标签之间的一致性,算的是一个样本的误差
2.3 代价函数(评分函数 Score Function)
简述:原始数据到类别分值的映射,是所有样本误差的平均,也就是损失函数的平均
2.4 目标函数(target function)
简述:在代价函数中寻找最小化的损失函数。可理解为也就是代价函数 + 正则化项
总结:
线性回归中的定义了方程组: Xw = y,其中(xi,yi)是给定的,不能修改,但是我们可以基于数据不断的调整W矩阵中每一个参数,使得这个函数得到的结果与训练集中的图像的真实类别一致,即评分函数或称为代价函数在正确的分类的位置上应该得到较高的的得分。
2.5 优化方法
2.5.1 梯度下降法(Gradient Descent)
简述:梯度下降是一种迭代算法,迭代中寻找使目标函数极小化的x值。此处的f(x)是具有一阶连续偏导数的函数。而在实际应用中,由于负梯度方向是使函数值下降最快的方法,于是我们的目标就是在每次迭代之后,以负梯度更新x的值,从而达到减少函数值的目的。
2.5.2 牛顿法(Newton’s Method)
简述:核心与梯度下降法类似,不同之处在于f(x)具有二阶连续偏导数。每次迭代计算完梯度值后求解目标函数的海赛矩阵的逆矩阵。
对比梯度下降法
优点:
- 收敛速度快
- 二阶收敛
缺点:
- 要计算Hessian矩阵,而矩阵有可能是非正定的
- 计算量巨大,设计矩阵
- 可能导致牛顿方向不是下降的。
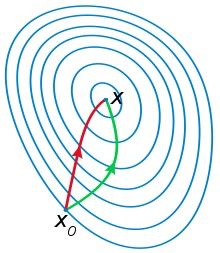
红色的是牛顿法的迭代路径
绿色的是梯度下降法的迭代路径
2.5.3 拟牛顿法(Quasi-Newton Methods)
简述:核心与牛顿法相似,因为牛顿法需要计算海赛矩阵的逆矩阵较为复杂,此方法则用一个n阶矩阵近似的代替海赛矩阵的计算。
2.6 线性回归的评估指标
2.6.1 均方误差MSE(Mean Squared Error)
对于简单的线性回归,目标是找到a,b 使 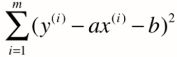 尽可能小,最终得到的衡量标准是:
尽可能小,最终得到的衡量标准是:
实际上就是 真实值 - 预测值 然后平方之后求和。
2.6.2 均方根误差RMSE(Root Mean Squared Error)
对于2.6.1的公式有一个问题就是会导致量纲的问题,因为对其做了平方的缘故,例如万元的房价变成万元平方的房价导致数据极大,这里对均方误差进行开根,使量纲相同
2.6.3 平均绝对误差MAE(Mean Absolute Error)
最后这个是另一种思路,用绝对值代替平方的形式,有点类似p1 与 p2 正则化的区别,不过没有平方:
三、Sitkit-learn 参数详解
这里拿最简单鸢尾花(IRIS)数据做最基础的讲解对象
简述一下操作步骤:
1. 导入数据。
2. 查看数据格式,分析其属性,选取特征,也可以称为简易版的特征工程。
3. 将数据分成训练集和测试集。简单的做法用交叉验证降低过拟合问题。
4. 查看数据是否有缺失或者离群样本,对这类数据进行剔除或者替换。
5. 建立学习模型并设置好参数,对训练集数据进行学习。
6. 模型完成之后,对训练集与测试集都计算其准确率。
7. 若有需要,则可以进行模型替换、优化等等进阶操作
8. 预测新样本。
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
X_train, X_test, y_train, y_test = train_test_split(
iris_dataset['data'], iris_dataset['target'], random_state=0)
print('X_train.shape:', X_train.shape)
print('y_train.shape:', y_train.shape)
print('X_test.shape:', X_test.shape)
print('y_test.shape:', y_test.shape)
# create dataframe from data in X_train
# label the columns using the strings in iris_dataset.feature_names
iris_dataframe = pd.DataFrame(X_train, columns=iris_dataset.feature_names)
print('iris_dataframe:\n', iris_dataframe.head())
# create a scatter matrix from the dataframe, color by y_train
pd.plotting.scatter_matrix(iris_dataframe, c=y_train, figsize=(15, 15),
marker='o', hist_kwds={'bins': 20}, s=60,
alpha=.8)
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print("Test set score: {:.2f}".format(knn.score(X_test, y_test)))