Structural Deep Clustering Network 基于GNN的深度聚类算法 WWW2020

论文链接：https://arxiv.org/abs/2002.01633
代码与数据集链接：https://github.com/lxk-yb/SDCN

摘要

聚类是数据分析中一个基础任务。最近，深度聚类（从深度学习方法中获取到主要的灵感）取得了领先的效果，并且吸引了很多的注意力。目前的深度聚类方法一般通过深度学习强大的表示能力提升聚类的结果，例如，自动编码器表明，对聚类来说学到一个有效的表示是必须的。深度聚类方法的要点一般在于能够从数据本身抽取出有用的表示，而不是数据的结构，这（因此数据的结构）在表示学习中很少受到关注。受到GCN成功编码图结构的启发，我们提出了一个结构化的深度聚类网络（SDCN），用来将结构化的信息整合到深度聚类中。具体来说，我们设计了一个（delivery operation）传送操作，用以把被自动编码器学到的表示传送到对应的GCN层，然后使用一个双重的自监督机制去统一这两个不同的深度神经结构，并且引导整个模型的更新。通过这种方法，这个多层数据结构，从低阶到高阶，就自然的和由自动编码器学到的表示结合在一起。比如，通过传送操作，GCN将autoencoder指定的表示改进为高阶图正则化约束，autoencoder有助于缓解GCN中的过平滑问题。通过综合的实验，我们表明了我们提出的模型可以一直比其他当前最好的工作好。

1、引言

随着深度学习的突破，神经网络在聚类等许多重要任务上取得了巨大成功，深度聚类引起了人们的广泛关注。深度聚类的基本思想是将深度学习强大的表征能力融入到聚类的目标中。因此，有效的学习数据的表征是深度聚类的关键前提。

尽管深度聚类取得了成功，但现有的工作[1][2][3][4]通常只关注数据自身的特性，在学习表征时很少考虑数据的结构。值得注意的是，在数据表征领域，考虑数据样本之间关系的重要性已经被以往的文献和结果所公认。这种结构揭示了样本之间潜在的相似性，从而为学习表征提供了有价值的指导。一种典型的方法是谱聚类，它将样本作为加权图中的节点，利用数据的图结构进行聚类。

最近，新兴的图卷积网络（GCN）同时对图结构和节点属性进行了编码，用于节点表征。目前已经有一些基于GCN的图数据聚类方法[5][6]，他们通过重构图的邻接矩阵来保持数据间的结构，但是这类方法缺少了对数据自身的特性的关注。因此我们考虑如何在保持现有深度聚类框架优点的同时，加入结构化信息。

2、模型结构

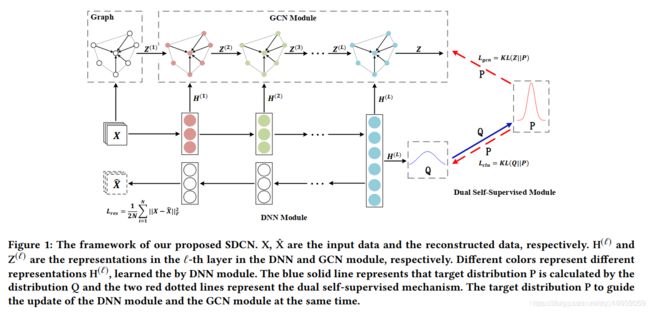
为了引入数据间的结构信息，在初始化模型之前，我们首先基于原始数据计算出一个K最近邻图。这个图会被作为GCN模块的输入。整个模型大概包括三部分：深度神经网络模块，图卷积模块和双重自监督模块。
在这个模型中，$X$是输入数据，$\hat{X}$是输出数据，$H^{(L)}$是经过$L$层DNN的输出，$Z^{(L)}$ 是经过$L$层GCN的输出，$P$是目标分布，$Q$是节点的类别分布。

3、模型详解

3.1、KNN Graph

KNN是有监督学习的K近邻的机器学习算法，K值是最近的K个样本的意思；它的思想是 ‘近朱者赤近墨者黑’，如果空间中某些样本具有相近的特征属性（样本距离比较近），我们可以认为它们的目标属性Y是相近的。我们可以用已有的最近K个样本的目标属性来预测（分类：加权多票表决，回归：加权均值）待测样本的目标属性。

在计算相似度矩阵S之后，选择每个样本的前K个相似度点作为其邻居，以构造无向K最近邻图。对于非图类型的数据，基于原始数据计算出一个K最近邻图，以此得到原始数据的之间的约束关系，形式为邻接矩阵。文中提到了两种近期最受欢迎的构造KNN图的方法：
1、Heat Kernel：
$$S_{ij}=e^{-\frac{||x_i-x_j|{|}^2}{t}}$$
2、Dot-product：
$$S_{ij}=x_j^T{x}_i$$

3.2、DNN Module

在本文中，使用基本的自动编码器来学习原始数据的表示，以便适应不同种类的数据特征。
其中，编码器encoder表示为：$$H^{(l)}=\varphi (W_e^{(l)}{H}^{(l-1)}+b_e^{(l)})$$解码器decoder表示为：$$H^{(l)}=\varphi (W_d^{(l)}{H}^{(l-1)}+b_e^{(l)})$$其中原始数据特征矩阵为$H^{(0)}$，同时$W$,$b$分别代表编码器和解码器的权重和偏置。

深度神经网络模块主要是利用自编码器学习数据自身的特性，损失函数为解码器的重构数据和原始数据之间的误差：
$$L_{res}=\frac{1}{2N}\sum _{i=1}^N||x_i-{\hat{x}}_i|{|}_2^2=\frac{1}{2N}||X-\hat{X}|{|}_F^2$$

3.3、GCN Module

图卷积模块主要是将图卷积层学到的GCN特定表征和自编码器学到的特征表征进行结合，然后通过在KNN图上进行传播学习到结构信息。

此模块说明了如何将DNN模块生成的结果应用到GCN模块中。 一旦将DNN模块学习到的结果集成到GCN中，则此时GCN通过迭代所生成的结果将同时包含两部分信息：图中节点的拓朴关系和节点自身特征，这将有利于图聚类任务，即数据本身和数据之间的关系。 特别是在权重矩阵W的情况下，可以通过以下卷积运算来获得GCN的第layer层学习到结果：$$Z^{(l)}=\varphi ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{Z}^{(l-1)}{W}^{(l-1)})$$这就是常规的GCN形式，以切比雪夫不等式的一阶近似作为卷积核对图进行卷积操作。

与标准图卷积层不同，我们的图卷积模块为了同时学习到GCN的表征和自编码器的表征，引入了一个传递算子，它将两个表征进行加权求和：$${\tilde{Z}}^{(l-1)}=(1-\epsilon )Z^{(l-1)}+\epsilon H^{(l-1)}$$然后再传入标准图卷积层中学习结构信息,（作者在文章中提到一般加权比重为0.5，即$\epsilon =0.5$）：$$Z^{(l)}=\varphi ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{\tilde{Z}}^{(l-1)}{W}^{(l-1)})$$

因为每个DNN都学习了不同的表示形式层，为了尽可能保留信息，从每个DNN层学到的表示转换为相应的GCN层进行信息传播，这也就解释了上面提到的网络架构中，每一层都要进行信息的融合
第一层为：$$Z^{(1)}=\varphi ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}X{W}^{(1)})$$最后一层：$$Z=softmax({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{Z}^{(L)}{W}^{(L)})$$这样我们就可以为自编码器中每一层学习到的表征都加入结构信息，同时保留自编码器学习数据自身特性的作用。

3.4、Dual Self-Supervised Module

现在已经在神经网络架构中将自动编码器与GCN连接起来。 但是，它们不是为聚类而设计的。 基本上，自动编码器主要用于数据表示学习，这是一种无监督的学习方案，而传统的GCN则处于半监督的学习方案。 它们都不能直接应用于聚类问题。 在这里，提出了一个双重自我监督模块，该模块将自动编码器和GCN模块统一在一个统一的框架中，并有效地端对端地训练了这两个模块以进行聚类任务的学习。

对于第$i$个样本和第$j$个聚类，使用Student的t分布作为内核来测量数据表示$h_i$和聚类中心向量${\mu }_j$之间的相似性，如下所示：$$q_{ij}=\frac{(1+||h_i-{\mu }_j|{|}^2/v{)}^{-\frac{v+1}{2}}}{{\sum }_{j^{\prime }}(1+||h_i-{\mu }_{j^{\prime }}|{|}^2/v{)}^{-\frac{v+1}{2}}}$$其中$h_i$是$H(L)$的第$i$行，${\mu }_j$是K-means在训练前自动编码器学习的表示形式上的初始化，$v$是学生$t$分布的自由度。 可以将$q_{ij}$视为将样本$i$分配给聚类$j$的概率，即软分配。 我们将$Q=[q_{ij}]$视为所有样本分配的分布。

在获得聚类结果分布$Q$之后，我们旨在通过从高可信度分配中学习来优化数据表示。 具体来说，我们希望使数据表示更接近聚类中心，从而提高聚类凝聚力。 因此，我们计算目标分布$P$如下：$$p_{ij}=\frac{q_{ij}^2/f_j}{{\sum }_{j^{\prime }}{q}_{i{j}^{\prime }}^2/f_{j^{\prime }}}$$$$f_j=\sum _i{q}_{ij}$$在目标分布$P$中，对$Q$中的每个分配进行平方和归一化，以便分配具有更高的置信度，采用KL散度来比较两类概率：$$L_{clu}=KL(P||Q)=\sum _i\sum _j{p}_{ij}\log \frac{p_{ij}}{q_{ij}}$$通过最小化$Q$和$P$分布之间的KL散度损失，目标分布$P$可以帮助DNN模块学习更好的聚类任务表示，即使数据表示围绕聚类中心更近。 这是一种自我监督机制，因为目标分布$P$由分布$Q$计算，并且$P$分布监督依次更新分布$Q$。

至于训练GCN模块，一种可能的方法是将聚类分配视为真实标签。 但是，此策略将带来噪音和琐碎的解决方案，并导致整个模型崩溃。 如前所述，GCN模块还将提供聚类分配分布$Z$。因此，我们可以使用分布$P$来监督分布$Z$，如下所$$L_{gcn}=KL(P||Z)=\sum _i\sum _j{p}_{ij}\log \frac{p_{ij}}{z_{ij}}$$目标函数有两个优点：
（1）与传统的多分类损失函数相比，KL散度以更“温和”的方式更新整个模型，以防止数据表示受到严重干扰。
（2）GCN和DNN模块都统一在同一优化目标中，使得它们的结果在训练过程中趋于一致。 由于DNN模块和GCN模块的目标是近似目标分布P（在两个模块之间具有很强的联系），因此我们将其称为双重自监督机制。

整个模型的整体损失函数为：$$L=L_{res}+\alpha L_{clu}+\beta L_{gcn}$$其中,$\alpha$是平衡原始数据聚类优化和局部结构保存的超参数，$\beta$是控制图卷积模块对嵌入空间干扰的系数。通过对这个损失函数的优化，我们可以以端到端的方式更新整个模型。

3.5、算法流程

3.6、理论分析

我们还进行了一些理论分析来证明我们提出的模型的优越性：一是GCN模块可以为自编码器学习到的表征施加二阶图正则，相当于为自编码器表征提供了结构信息；

二是传递算子可以缓解GCN中出现的过拟合现象。

4、实验

我们在六个数据集上分别和现有的深度聚类算法以及基于GCN的聚类算法进行了比较，并做了变体实验，传播层数实验，传递算子参数实验，K敏感性实验等。
下图为变体实验：

下图为数据集信息：

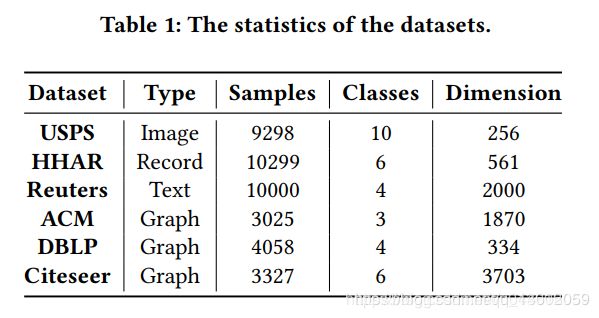
下图为对比实验结果：

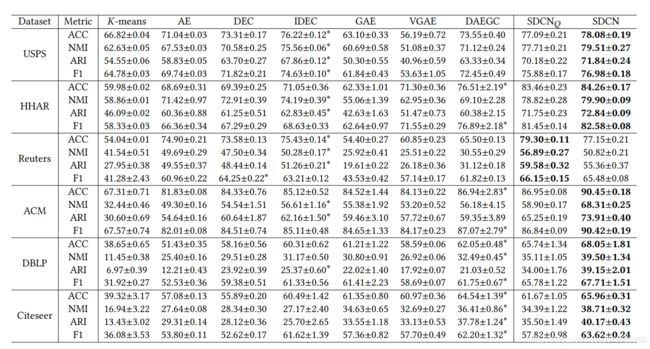
下图为传递算子参数实验：

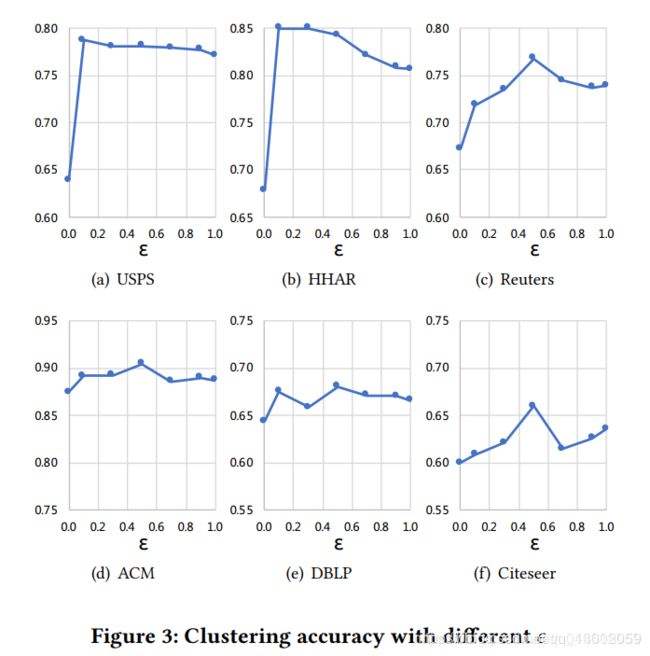
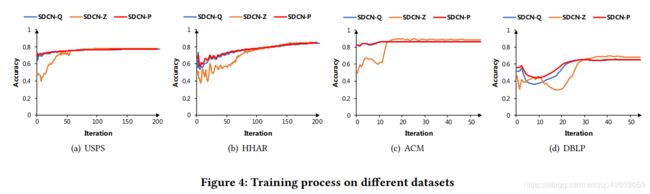
下图为训练轮次实验：

下图为K敏感性实验：

5、参考文献

https://zhuanlan.zhihu.com/p/107648120
[1] Bo Yang, Xiao Fu, Nicholas D Sidiropoulos, and Mingyi Hong. 2017. Towards k-means-friendly spaces: Simultaneous deep learning and clustering. In ICML. 3861–3870.

[2] Junyuan Xie, Ross Girshick, and Ali Farhadi. 2016. Unsupervised deep embedding for clustering analysis. In ICML. 478–487.

[3] Xifeng Guo, Long Gao, Xinwang Liu, and Jianping Yin. 2017. Improved deep embedded clustering with local structure preservation. In IJCAI. 1753–1759.

[4] Zhuxi Jiang, Yin Zheng, Huachun Tan, Bangsheng Tang, and Hanning Zhou.2017. Variational deep embedding: An unsupervised and generative approach to clustering. IJCAI (2017).

[5] Thomas N Kipf and Max Welling. 2016. Variational graph auto-encoders. arXiv preprint arXiv:1611.07308 (2016).

[6] Chun Wang, Shirui Pan, Ruiqi Hu, Guodong Long, Jing Jiang, and Chengqi Zhang.

Attributed Graph Clustering: A Deep Attentional Embedding Approach. IJCAI (2019).