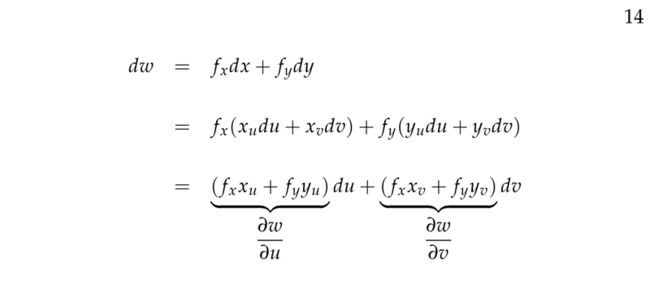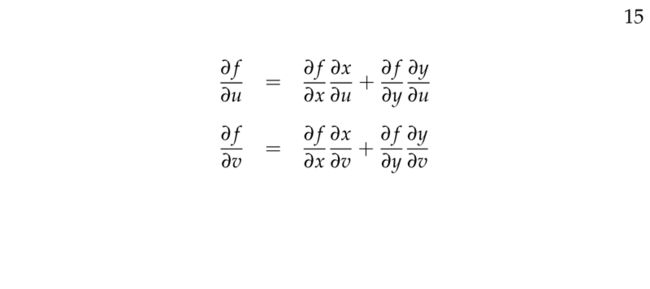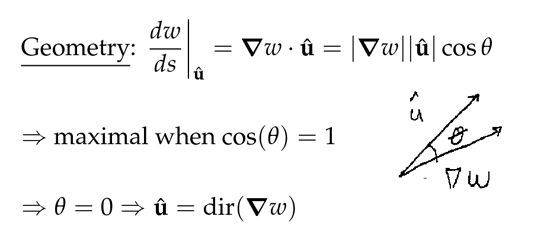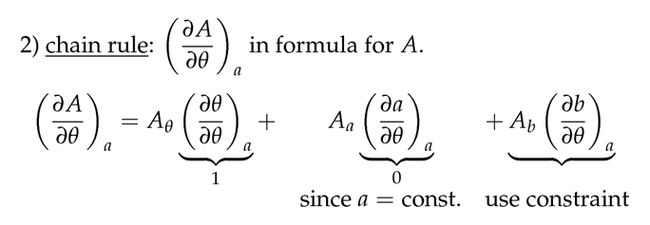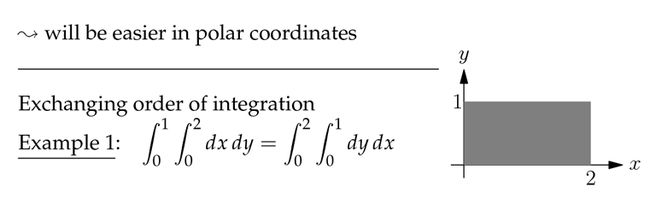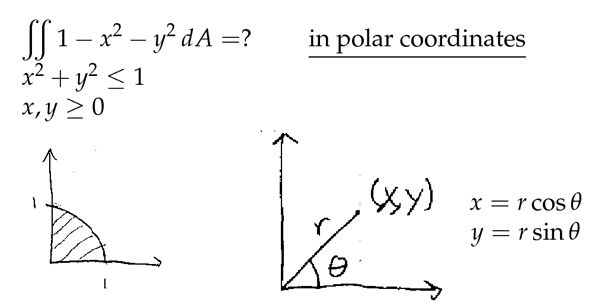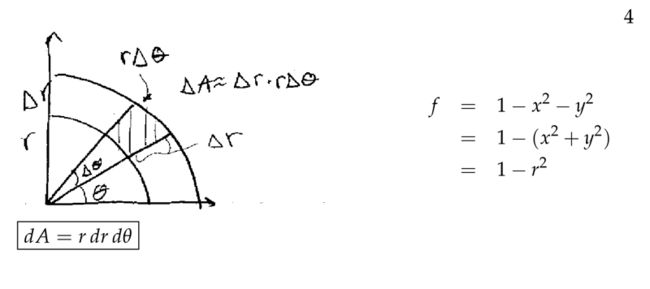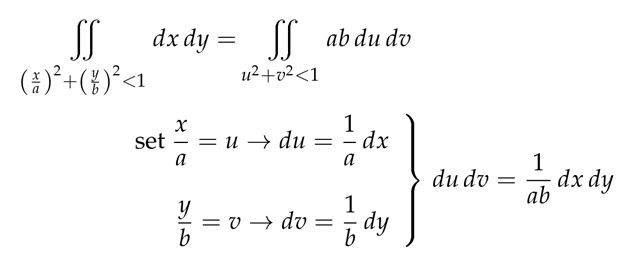Multivariable Calculus 总结（第一部分）

Dot Product

Because the dot product results in a scalar, it is also called the scalar product.

algebraic view of dot product

给定两个向量 a⃗ =⟨a1,a2,a3⟩ ， b⃗ =⟨b1,b2,b3⟩ ，它们的点积定义如下：

a⃗ ⋅b⃗ =a1b1+a2b2+a3b3

properties of dot product

下面属性的证明大部分都是一些代数计算，根据点积的 algebraic view，你可以很轻松地证明出来。

geometric view of dot product

下面定理用 The Law of Cosines 来证明，详细步骤参考：Dot Product

a⃗ ⋅b⃗ =|a⃗ ||b⃗ |cos(θ)

这个公式通常不是用来计算点积，而是找出2个向量之间的角。有了这个公式，点积可以让我们很容易地判断出2个向量是否 perpendicular or parallel. （When two vectors are perpendicular to each other we say they are orthogonal.）

Now, if two vectors are orthogonal then we know that the angle between them is 90 degrees:

a⃗ ⋅b⃗ =0

Likewise, if two vectors are parallel then the angle between them is either 0 degrees (pointing in the same direction) or 180 degrees (pointing in the opposite direction):

a⃗ ⋅b⃗ =|a⃗ ||b⃗ |  (θ=0)a⃗ ⋅b⃗ =−|a⃗ ||b⃗ |  (θ=180)

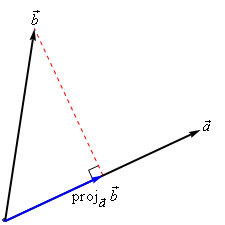
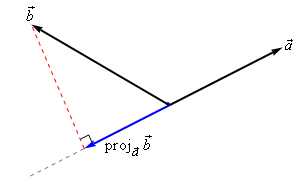
Projections

下面2幅图是 the projection of b⃗  onto a⃗  , denoted by proja⃗ b⃗ 

There is an nice formula for finding the projection of b⃗  onto a⃗  . Here it is,

proja⃗ b⃗ =a⃗ ⋅b⃗ |a⃗ |2a⃗ 

Note that we also need to be very careful with notation here. The projection of a⃗  onto b⃗  is given by:

projb⃗ a⃗ =a⃗ ⋅b⃗ |b⃗ |2b⃗ 

Cross Product

We should note that the cross product requires both of the vectors to be three dimensional vectors. The result of a dot product is a number and the result of a cross product is a vector!

Area and Determinants

下图中是第一种求三角形面积的方式。

我们知道点积中的公式是 cosθ ，而上图中是 sinθ ，那么如何转化一下它们呢？下图中的方法实现了转化，图中错误的部分我用红线标出了。它的主要思想如下：

1、把向量 A⃗  旋转90度，因此得到了 sinθ=cosθ′
2、由于是旋转，所以向量 A⃗  的长度不变
3、通过旋转，我们得到了 A′,θ′,B ，可以应用点积公式了

上图中的最终结果实际上就是 a1b2−a2b1=det(A⃗ ,B⃗ )=∣∣∣a1b1a2b2∣∣∣ ，如果你想用 determinant 求面积，你需要加上绝对值，由于面积始终为正的。还有一点就是，determinant 的绝对值是平行四边形的面积，三角形应该乘以1/2

cross product 的定义

下图中是2个向量的 cross product 的定义：

下图中是关于 cross product 的方向与长度的定理：

关于 cross product 还有2个知识点：

1、 A⃗ ×B⃗ =−(B⃗ ×A⃗ )
2、根据1，可得 A⃗ ×A⃗ =0

Volumes and Determinants

determinant 同样可以求体积：

下图中是用另一种方法来求体积，如果你一直算下去，你会发现它实际上就是 determinant，即： A⃗ ⋅(B⃗ ×C⃗ )=det(A⃗ ,B⃗ ,C⃗ )

Equations of Planes

如下图所示，已知平面上的3个点，求出表示平面的方程。在上面我们已经知道 determinant 可以求体积，而平面的体积为0，所以有下图中的公式求平面方程。

我们还用上面的图形，第二种方式求解方式： P1P→⋅(P1P2→×P1P3→)=0 ，你会发现它实际上就是 determinant

---

一个平面的公式形式为： ax+by+cz=d ，当我们知道了一个平面的 normal vector 以后，就可以确定无数多个平行的平面，如果再给出平面经过哪个点以后，就可以确定一个具体的平面了。

下图是一个具体的例子，它的 normal vector 为 N⃗ =⟨1,5,10⟩ ，并且通过 P0=(2,1,−1) ，用点积就可以求出平面的方程了。

其实不难发现，normal vector 就是平面公式左面的系数，至于右面的值是什么，取决于你经过哪个点，然后把它代入就可以求出来了，比如，平面经过原点，因此把 x=y=x=0 代入就知道右面的值也为0了。

Linear Systems and Planes

关于线性方程组（假设有3个平面）的解有以下几种可能：

1、没有解。3个平面平行，或者其中的2个平面相交的直线平行与第3个平面（第3个平面不包含这条线）

2、1个解。其中的2个平面相交的直线与第3个平面也相交， AX=B 的解为 X=A−1B

3、无穷多个解。3个平面重合，或者第3个平面包含其中的2个平面相交的直线

下图就是有一个解的例子：

---

接下来，我来总结一下 Homogeneous and Inhomogeneous Systems 这篇文章的内容：

The linear system Ax=b is called homogeneous if b=0 ; otherwise, it is called inhomogeneous. 下面是2个定理：

Theorem 1. Let A be an n×n matrix.

• |A|≠0⇒Ax=b has the unique solution, x=A−1b
• |A|≠0⇒Ax=0 has only the trivial solution, x=0

Theorem 2. Let A be an n×n matrix.

• |A|=0⇒Ax=0 has non-trivial (i.e., non-zero) solutions.
• |A|=0⇒Ax=b usually has no solutions, but has solutions for some b .

定理一中的 A−1=1det(A)adj(A) ，由于 |A|≠0 ，即 det(A)≠0 ，我们代入公式就可以验证结果了。

定理二的证明文章中已经给出了详细的步骤，我们假设 A 包含3个行向量 a⃗ ,b⃗ ,c⃗  ，也就是3个平面各自的 normal vector，由于 det(A)=a⃗ ⋅(b⃗ ×c⃗ )=0 ，即这3个向量形成的体积为0，所以它们共面，得到这个结论以后，剩下的就很好证明了，看文章的步骤就 OK 了。

用 second derivative 测试判断 local minimum, maximum and saddle point

At a critical point (x0,y0) of f , let A=fxx(x0,y0) , B=fxy(x0,y0)(=fyx(x0,y0)) and C=fyy(x0,y0) , so:

• If AC−B2>0 and A>0 , local minimum.
• If AC−B2>0 and A<0 , local maximum.
• If AC−B2<0 , saddle point.
• If AC−B2=0 , can’t conclude.

Total Differentials and the Chain Rule

f(x,y,z) 的全微分：

df=fxdx+fydy+fzdz=∂f∂xdx+∂f∂ydy+∂f∂zdz

N.B. 一定要区分开 d 和 ∂ ，它们分别代表着全微分和偏微分，当你用偏微分时，切记它不能做简化，比如：

对于全微分我们可以： dfdxdxdt=dfdt ，但是对于偏微分来说，你不可以这样做： ∂f∂x∂x∂t≠∂f∂t

df 不是 Δf ，上面的全微分你可以解释成 x,y,z 的 infinitesimal 变化怎么影响 f ，但是 Denis Auroux 教授更喜欢把它解释成 tangent approximation， Δf≈fxΔx+fyΔy+fzΔz ，当这些 Δ 变量趋于0时，约等于就变成了等于。

下面4幅图是关于 Chain Rule 更有趣的例子：

Denis Auroux 教授给我们用一种更好的方式解释了标号为15的那幅图： f 的变化取决于变量 x 和 y , 而 x 和 y 的变化又取决于变量 u 和 v ，所以当我们想找出 f 与 u 之间的变化关系时，即 ∂f∂u ，我们可以把它解释成 u 的变化会影响到变量 x 和 y ，接着变量 x 和 y 的变化会影响到 f ，所以有标号为15的那幅图的公式。

实际上整个微积分学科就是一门研究变化的科学，研究变量之间是如何相互影响的，某个变量的变化如何影响到另一个变量的变化。我们也可以把变量拆分成我们想要研究的变量的关系，比如，目前我们知道 f 是关于 x 和 y 的函数，而变量 t 影响着变量 x 和 y ，因此我们可以拆分 x 和 y 是关于变量 t 的函数，从而研究 f 与 t 的关系。

梯度和方向导数

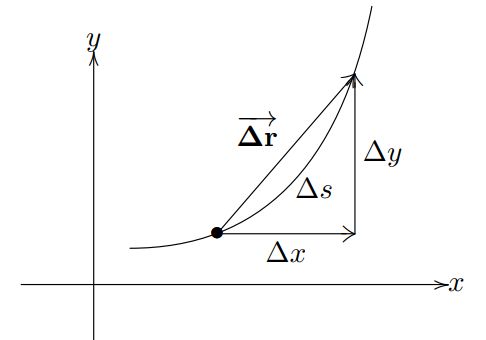
Velocity, speed and arc length

本小节根据 Velocity, speed and arc length 做出总结。

我们用向量 r⃗ (t)=x(t)i⃗ +y(t)j⃗ =⟨x,y⟩ 来 trace 上图中的那个曲线轨迹，如果起始点在原点，那么它就是一个 position vector. 我们用 s 表示 arc length. 上图是二维空间的一个例子，三维空间也是一样的，只不过是增加了一个维度。给出了 notation，根据上图我们有：

Δs≈|Δr|→=(Δx)2+(Δy)2−−−−−−−−−−−−√

我们对上式2边同除以 Δt ，得到：

ΔsΔt≈∣∣∣∣Δr→Δt∣∣∣∣=(ΔxΔt)2+(ΔyΔt)2−−−−−−−−−−−−−−−−√

Taking the limit as Δt→0 gives:

dsdt=∣∣∣∣dr→dt∣∣∣∣=(dxdt)2+(dydt)2−−−−−−−−−−−−−−−√=|v⃗ |=speed

上式中，我们得到了 speed，可以看出它只有大小，没有方向，也就是标量。而关于 velocity 的公式为： dr→dt=v⃗ (t)=x′(t)i⃗ +y′(t)j⃗ =⟨x′,y′⟩=velocity ，velocity 是个向量，它是一个 tangent vector，在任何时候都与轨迹相切。

The unit tangent vector is a unit vector in the same direction as the tangent vector. We usually denote it T⃗  . We compute it by dividing the tangent vector by its length. Here are several ways of writing this.

T⃗ =v⃗ |v⃗ |=dr⃗ /dtds/dt=v⃗ ds/dt

Gradient

下面是一个非常重要的定理：

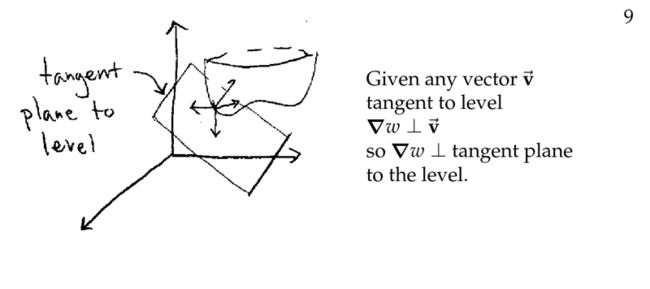
Gradients are orthogonal to level curves and level surfaces.

level curves 也就是2个变量的函数的 contour line; level surfaces 就是：

A level surface, or level set of a function of three variables, f (x, y, z), is a surface of the form f (x, y, z) = c, where c is a constant. The. function f can be represented by the family of level surfaces obtained. by allowing c to vary.

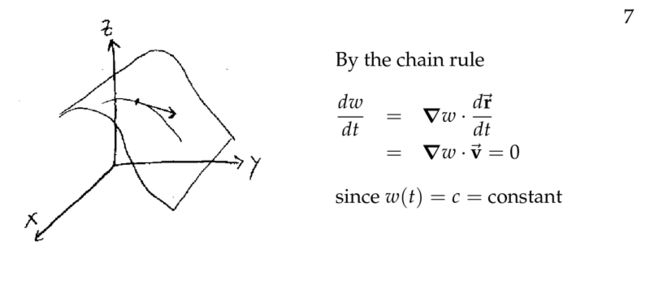
从上面的定义可以看出，level curves 或者 level surfaces 上的函数值不发生变化。下面，让我们来证明上面的定理。

假设函数 w=w(x,y,z) ，而函数 x=x(t),y=y(t),z=z(t) ，根据链式法则：

dwdt=wxdxdt+wydydt+wzdzdt=∇W⋅dr⃗ dt

由于函数 w 有3个变量，因此是 level surface; 上面的 dr⃗ =⟨dx,dy,dz⟩ 用来表示(track) level surface 上的任意一段轨迹。由于 level surfaces 上的函数值不发生变化，可得：

上图中，只是给出了一条轨迹，而如果想要的话，我们可以在整个 level surface 上任意画轨迹，因此 level surface 上的每个点我们都可以找到 velocity vector，与 level surface 相切。因此得到下图的结论：

我们可以利用上面的定理，可以很容易地找出 Tangent Plane. 下图就是一个例子：

本文上面 Equations of Planes 这一小节给出了法向量与平面公式之间的关系。

Directional Derivatives

本小节总结来自于 Directional Derivatives

我们已经知道偏导是 x轴方向( i⃗  ) 或 y轴方向( j⃗  ) 的导数，而方向导数就是任意给定的单位向量 u⃗  的方向的导数。The directional derivative of w at P0 in the direction u⃗  is defined as

dwds|p0,u⃗ =limΔs→0ΔwΔs=∇w(P0)⋅u⃗ 

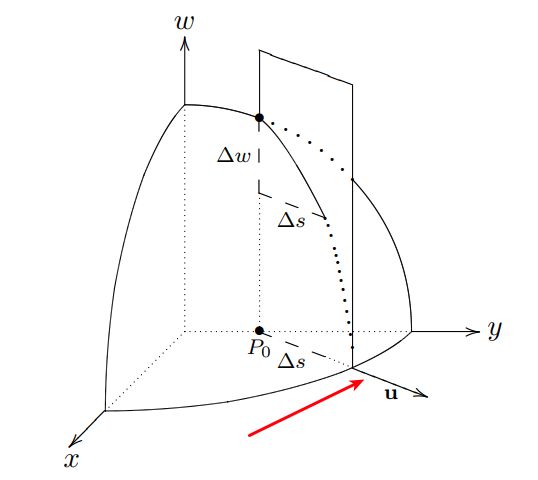
上文中给出了上述公式详细的证明，很简单，看一下就明白了。下面我给出教授在课上的证明过程：

教授把下图中红色箭头所指的那部分当作是一段轨迹，因此有： dr⃗ ds=u⃗ ^ ，向量 u⃗  之所以是单位向量，由于轨迹是条直线，也就是说， ds 是 dr⃗  的长度，它们相除我们得到了单位向量。

由于我们关心的是 dwds ，根据链式法则可得：

dwds=dwdr⃗ ⋅dr⃗ ds=⟨∂w∂x,∂w∂y,∂w∂z⟩⋅dr⃗ ds=∇w⋅u⃗ ^

下图解释了为什么梯度方向是函数上升最快的方向：

Lagrange Multipliers

lagrange multipliers 用于解决带有约束的优化问题。下面是对 lagrange multipliers 整个方法内容的定义：

So, let’s get things set up. We want to optimize (i.e. find the minimum and maximum value of) a function, f(x,y,z) , subject to the constraint g(x,y,z)=k . Again, the constraint may be the equation that describes the boundary of a region or it may not be. The process is actually fairly simple, although the work can still be a little overwhelming at times.

上图来源于 Lagrange Multipliers，同时文章中也有几个例子教我们如何使用 lagrange multipliers.

教授在课上也并没有对 Lagrange Multipliers 给出太 formal 的证明，他说的我大概理解就是：比如在没有约束的情况下，我们需要找出 critical points，从而找出 extrema. 同样的道理，在有约束的情况下，要让被优化的函数在 level set 上找出 critical points，从而当函数向任意方向在 level set 上移动时，使 df=0 .

上面的表述逻辑比较乱，供我自己找出关键点，Maybe….. Proof of Lagrange Multipliers

Constrained Differentials

其实整个 lecture 都在讲在变量之间有约束的情况下，如何找出各个变量之间的变化关系（the rate of change）.

当我们求解应用题目时，比如我们得到一个函数： f(x,y,z) , 我们一定要注意这3个变量之间是否完全独立或是它们之间存在关系。然后在找出它们之间的变化关系。

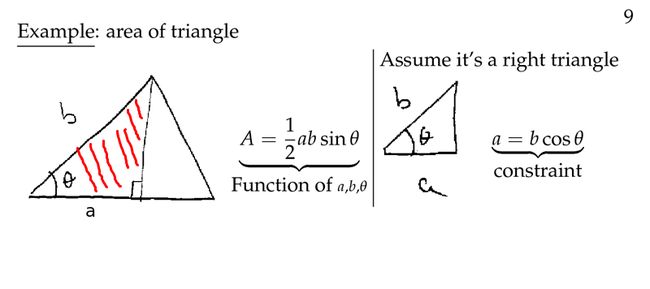
教授整整花了半节课的时间来讲解下图这个例子。例子链接

我们想知道上图中红色区域面积 A 与 θ 之间的变化关系，即 ∂A∂θ ，一共分为以下2种情况：

1. 假设三角形为直角三角形，因此这就存在上图右侧的隐式约束，在这种情况下，还分为以下2种情况：

   • 保持 a 不变，即求解 (∂A∂θ)a
   • 保持 b 不变，即求解 (∂A∂θ)b

2. 没有任何约束，也就是变量 a,b,θ 之间是相互独立的，所以我们只需要求解 (∂A∂θ)a,b

对于上面2种情况，教授在课上给出了求解。这里我只说一下我个人对下图中这种解法的理解：

上面的解法其实和上文中的 Total Differentials and the Chain Rule 一样的道理，只不过现在有了约束，就有了不一样的 notation. 变量 A 被变量 a,b,θ 影响着，而变量 θ 又影响着变量 a,b,θ ，因此有了上面的链式法则求解。

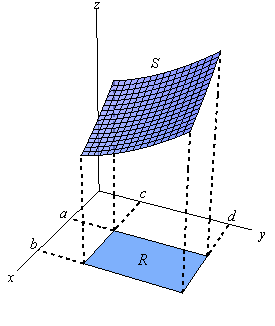
Double Integrals

正如下面2幅图所示一样，double integral 可以用来求解体积，它的公式如下所示，如果微分学的好，下面公式一下就可以理解了，没什么好说的！

Volume=∬Rf(x,y)dA

上面的公式是最简洁抽象的一种方式，那么在具体的求解过程中，我们有2种具体的思维方式：

1、想像一个平行于 y,z 轴的平面，沿着 x 轴横扫，因此我们有如下公式，实际上中括号内部的公式表示的是 slices 的面积，乖上 dx 以后就是一个小的体积，然后沿着 x 轴方向积分。

∫ba[∫dcf(x,y)dy]dx

2、想像一个平行于 x,z 轴的平面，沿着 y 轴横扫，因此我们有如下公式，道理和上面相似。

∫dc[∫baf(x,y)dx]dy

其实上面的2个公式也叫做：iterated integrals, 上面的中括号是我为了便于理解写的，按照惯例，不用加，因此的来说为：

Volume=∬Rf(x,y)dA=∫dc∫baf(x,y)dxdy=∫dc∫baf(x,y)dxdy

理论上面2种方式都可以求解体积，但是有些时候，一个方法可能会比另一个方法更容易计算出体积来。

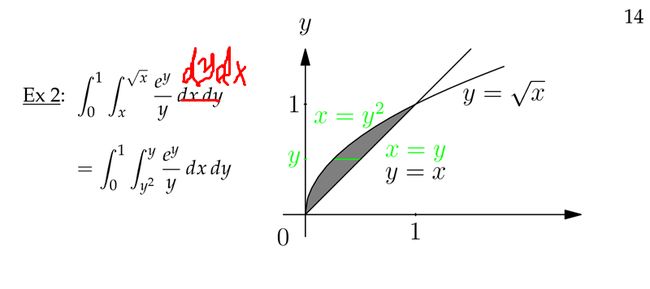
下面我来解释一下关于上述公式中积分边界的问题。它也分为2种情况：

1、长方形的区域 R . 正如下图所示，当你 slice 变量 x 时，变量 y 的范围并不随着变量 x 的变化而变化; 同样的道理，当你 slice 变量 y 时，变量 x 的范围并不随着变量 y 的变化而变化。因此在这种情况下，交换积分的顺序很简单，如下图所示。

2、任意形的区域 R . 从下图中可以看到，当你 slice 变量 x 时，变量 y 的范围随着变量 x 的取值而变化; 同样的道理，当你 slice 变量 y 时，变量 x 的范围也随着变量 y 的取值而变化。因此在这种情况下，交换积分的顺序就会变得复杂一些，如下图所示，下图中出现的错误我用红笔已经改过来了。

Double Integrals in Polar Coordinates

下图中左半部分虽然可以求出体积，但是计算积分的过程非常繁琐，因此我们把这个问题转换到极坐标上来求解。下图中的右半部分，是把 x,y 2 个变量转换成 r,θ 2个变量，即极坐标的形式。

转换了变量那么如何重新定义二重积分呢？下图是教授给出的一种更直观的解释，更正式的证明需要下面介绍到的 Jacobian，Change of Variables 中的例子2就是证明。. 因此我们可以得到： ∫π20∫10(1−r2)rdrdθ

看了很多的例子，根据经验来说，我个人觉得基于圆形的求解用极坐标的概率要大些。

Change of Variables

下面给出了变换变量的原因：

While often the reason for changing variables is to get us an integral that we can do with the new variables, another reason for changing variables is to convert the region into a nicer region to work with.

正如上面极坐标的那个例子一样，转换变量是为了让我们更容易地求出积分。我把变换变量的步骤归纳总结为以下3步：

1、 dx,dy vs du,dv

dA=dxdy 的含义就是 xy-coordinates 中待积分区域中的一小块面积，当我们想把变量 x,y 转换成 u,v 时，需要知道 uv-coordinates 平面中的 dA′=dudv . The Jacobian of the transformation x=g(u,v) , y=h(u,v) is:

∂(x,y)∂(u,v)=∣∣∣∣∣∂x∂u∂y∂u∂x∂v∂y∂v∣∣∣∣∣

上述公式中的右半部分是行列式。有了 Jacobian，我们就可以知道了 dA 与 dA′ 的关系了： dA=∣∣∣∂(x,y)∂(u,v)∣∣∣dA′ ，这个公式中的是绝对值符号。

2、用新的变量替代 integrand.

3、找出新变量相对应的边界。

我们只需要逐个边的转换即可，然后在新区域中找出新变量的范围。Change of Variables 中的例子3就是一个完整的例子。

注意：当把一个 ellipse 区域转换成一个圆时，可能不需要上面繁琐的步骤，你直接代入新的变量就可以，比如下图中的例子，由于下面的变量 x 只取决于变量 u ，因此可以直接得到 du 与 dx 的关系，变量 v,y 也是同样的道理。

Change of Variables 中的例子4也是关于 ellipse 的非常好的例子，它通过直接代入把 ellipse 的区域（变量 x,y ）转换成了圆形区域（变量 u,v ），然后由于求解积分对于极坐标来说更容易，它又转换成了极坐标（变量 r,θ ）.

积分在物理上的应用

Applications: Mass and Average Value

Mass Of Object

如何求出物体的 mass 呢？说成大白话就是：在 3D 中，就是对（ Δm= 每一无限小块的体积 × 每个无限小块对应的密度）积分; 在 2D 中，就是对（ Δm= 每一无限小块的面积 × 每个无限小块对应的密度）积分。用数学公式表达如下：

3D:Mass=∭RδdV2D:Mass=∬RδdA

正常情况下， δ 是关于变量 x,yand/orz 的函数; 但是如果各处的密度都相同，那么它就是常量，因此你可以把 δ 从积分中拿出来。

Average Value

在高中的时候，我们已经知道如何求出离散数据的平均值和它的加权平均值。有了积分技术，我们就可以求出连续数据的平均值了。在单变量微积分中，一个连续区间的平均值和加权平均值公式如下：

f¯=1b−a∫baf(x)dxweighted(f¯)=1∫baw(x)dx∫baf(x)w(x)dx

其实上面的公式很好理解，和离散数据集的道理一样，只不过积分使我们可以加上区间每一处的 f(x) 值，然后除以总数。在加权的情况下道理也一样，只不过每一处的 f(x) 值有了不同的权重，所以相应地乘上其权重，如果各处的权重相同，它就会变成上面的第1个公式。

在二重积分的情况下，求平均值的道理与单变量微积分一样，它的公式如下：

f¯=1∬RdA∬RfdA=1区域面积∬RfdAweighted(f¯)=1∬RδdA∬RfδdA=1区域Mass∬RfδdA

对上面公式的理解像单变量微积分一样，只不过现在是每一处无限小块的面积对应 f(x) 的值。

在三重积分的情况下，求平均值的道理也一样，它的公式如下：

f¯=1∭RdV∭RfdV=1区域体积∭RfdVweighted(f¯)=1∭RδdV∭RfδdV=1区域Mass∭RfδdV

Center Of Mass

在二重积分的情况下，它的公式如下：

(x¯,y¯)=(1∬RδdA∬RxδdA,1∬RδdA∬RyδdA)

在三重积分的情况下，它的公式如下：

(x¯,y¯,z¯)=(1∭RδdV∭RxδdV,1∭RδdV∭RyδdV,1∭RδdV∭RzδdV)

Moment of Inertia

For a point mass, m , the moment of inertia about the line is:

I=md2

where d is the distance from the mass to the line. (The letter I is a standard notation for moment of inertia.) If we have a distributed mass we compute the moment of inertia by summing the contributions of each of its parts. If the mass has a continuous distribution, this sum is, of course, an integral.

上面已经给出了转动惯量的定义，那么现在我们可以很容易地写出它的微分表达了。由于沿不同轴旋转会导致距离的不同，下图的例子是关于 y 轴的转动惯量，画线部分就是它的微分表达：

上图中是关于二重积分的，在 3D 中，道理也是一样的，公式如下：

Ix=∭R(y2+z2)δdVIy=∭R(x2+z2)δdVIz=∭R(x2+y2)δdV=∭Rr2δdV