【姿态估计】DeepPose: 基于深度神经网络的人体姿态估计 Human Pose Estimation via Deep Neural Networks

Alexander Toshev Christian Szegedy Google 1600 Amphitheatre Pkwy Mountain View, CA 94043 toshev,[email protected]

原文地址： https://arxiv.org/abs/1312.4659
引用请注明出处。

摘要

作者提出了一种基于深度神经网络（DNN）的人体姿态估计方法。姿态估计被公式化为针对身体关节的基于DNN的回归问题。作者提出了一系列这样的DNN回归量。这种方法能够产生高精度的姿态估计。该方法具有以整体方式推理姿态的优点，利用了深度学习的最新进展，并且具有简单但强有力的表述。作者在各种各样的真实世界图像的四个学术benchmark上与经典方法进行了比较，提供了详细的实证分析，有更好的表现。

1. 引言

人体姿态估计的问题（定义为人体关节的定位问题）在计算机视觉社群中受到了极大的关注。如 图1 所示，人们可以看到这个问题的一些挑战 ：有些关节很大，而有些关节小到几乎不可见，有些关节被遮挡（occlusions），此外还有捕捉背景的需要。该领域的历史工作的动力主要源于第一个挑战，即需要在大空间中搜索所有可能的关节姿态。基于部件的模型可以自然地模拟关节模型([16, 8]) 。近年来，已经提出了各种具有有效推理的模型([6, 19])。

图1 除了关节的极端可变性外，许多关节几乎看不见。在左图中可以猜测右臂的位置，因为能看到人体的其余部分并预测到人的动作或活动。同样，右侧人的左半身完全看不见。这些是整体推理需求的例子。DNN可以自然地提供这种推理。

然而，上述效率是以有限的表现力——局部检测器的使用为代价实现的，它在许多情况下检测单个部件，并且最重要的是通过仅对身体部位之间的所有相互作用的一小部分进行建模。这些限制，如图1所示，已经被发现，并提出了以整体方式推理姿态的方法[15, 21]但在现实问题上取得的成功有限。

在这项工作中，作者归纳了人类姿态估计的整体观点，并利用深度学习的最新进展提出了一种基于深度神经网络（DNN）的新算法。DNN在视觉分类[14]和目标定位[23, 9]等任务方面表现出色。然而，将DNN应用于铰接物体的精确定位的问题在很大程度上仍未得到解决。在本文中，作者试图阐明这个问题，并基于DNN提出简单而强大的整体人体姿态估计方法。

作者将姿态估计表示为联合回归问题，并展示如何在DNN设置中成功映射它。这种方法使用完整图像和7层通用卷积DNN作为输入将每个身体关节的位置进行回归。这种仿佛有两个优点。首先，DNN能够捕获每个身体关节的完整背景——每个关节回归器使用完整图像作为信号。其次，该方法比基于图形模型的方法更容易制定 - 无需明确设计零件的特征表示和检测器；无需明确设计模型拓扑和关节之间的交互。相反，作者表明可以为这个问题学习通用的卷积DNN。

此外，作者提出了一系列基于DNN的姿态预测器。这种级联能提高联合定位的精度。从初始姿态估计开始，基于完整图像，作者学习基于DNN的回归量，通过使用更高分辨率的子图像来改进联合预测。

作者对他们state of art级别的结果，或者超过state of art的结果显示于四种广泛使用的基准测试。作者表明，作者的方法在人的图像上表现良好，这些人在外观和关节方面表现出很强的变化。最后，作者通过跨数据集评估展示了泛化性能。

2. 相关工作

从计算机视觉的早期就提出了一般性地表达铰接物体，特别是人体姿态作为部件图形的想法[16]。Fishler和Elschlager提出了Pictorial Strictures（PSs）[8]方法，由Felzenszwalb和Huttenlocher [6] 使用距离变换技巧让这个方法易于实现。随后研究人员开发了具有实际意义的各种基于PS的模型。

然而，上述易处理的模型也具有以下限制：基于树的姿态模型具有简单的binary potential，这不依赖于图像数据。因此，最近的研究专注于丰富模型的代表能力，同时保持易处理性。之前这一目标的尝试是基于更丰富的部分探测器[19, 1, 4]。最近，研究人员提出了表达复杂关节关系的各种模型。杨和Ramanan [27] 使用部件的混合模型。Johnson和Everingham研究了在全模型尺度下具有多个PS的混合模型[13]。Tian等人在层次模型中捕获了更丰富的高阶空间关系[25]。捕获高阶关系的一种不同方法是通过依赖于图像的PS模型，这可以通过全局分类器来估计[26, 20, 18]。

由于以整体方式推理姿态的理论已经显示出有限的实用性。Mori和Malik [15] 尝试为每个测试图像找到一组标记图像中最接近的样本并转移关节位置。Shakhnarovich等人使用局部敏感哈希采用了类似的最近邻设置[21]。最近，Gkioxari等人 [10] 提出用于零件配置的半全局分类器。这个公式在在真实数据上已经显示出非常好的结果，但是，它基于线性分类器，其表达方式比作者的表达更少，并且仅在手臂上进行测试。最后，Ionescu等人采用了姿态回归的思想[11], 他们尝试去推理3D姿态。

与作者最接近的工作是使用卷积NN和邻域分量分析来回归代表姿态的嵌入点[24]，但是，这项工作不采用级联网络。级联DNN回归已被用于面部特征点识别的定位[22]。关于面部姿态估计的相关问题，Osadchy等 [17] 使用对比度损失采用基于NN的姿态embedding训练。

3. 姿态估计的深度学习模型

作者使用以下符号。为了表达姿态，作者在定义的姿态向量中编码所有 $k$ 个身体关节的位置 $y=(...,y_i^T,...{)}^T,i\in \{1,...,k\}$ ，其中 $y_i$ 包含第i个连接点的 $x$ 和 $y$ 坐标。带标签的图像是用 $(x,y)$ 表示，其中 $x$ 代表图像数据， $y$ 是ground truth。

此外，由于关节坐标是绝对图像坐标，因此要将它们标准化为限制人体或其部分的框 $b$ 。在一个简单的情况下，框可以表示完整的图像。这样的方框由其中心 $b_c\in {\mathbb{R}}^2$ 以及宽度 $b_w$ 和高度 $b_h$ 定义： $b=(b_c，b_w，b_h)$ 。然后连接点 $y_i$ 可以通过框中心进行平移，并通过框大小进行缩放，作者将其称为 $b$ 的归一化：

$$N(y_i;b)=\left[\begin{array}{cc}1/b_w& 0\\ 0& 1/b_h\end{array}\right](y_i-b_c)\text{\hspace{1em}(1)}$$

此外，作者可以对姿态向量 $N(y;b)=(...,N(y_i;b{)}^T,...{)}^T$ 的元素应用相同的归一化，从而得到归一化的姿态矢量。最后稍微滥用以下符号，作者使用 $N(x;b)$ 来表示边界框 $b$ 对图像 $x$ 的裁剪，这实际上是通过框来规范化图像。为简洁起见，作者用 $N(\cdot )$ 来表示归一化， $b$ 是完整的图像框。

图2 左：基于DNN的姿态回归的示意图。作者用相应的尺寸可视化网络层，其中卷积层为蓝色，而完全连接的层为绿色。作者不显示参数自由的层。右：在s个阶段，将精细化回归应用于子图像以改进前一阶段的预测。

3.1 基于DNN回归的姿态估计

在这项工作中，作者将姿态估计的问题视为回归，其中作者训练并使用函数 $\psi (x;\theta )\in {\mathbb{R}}^{2k}$ ，对于图像 $x$ ，该函数回归归一化的姿态向量，其中 $\theta$ 表示该模型的参数。因此，使用方程(1) 进行归一化变换，绝对图像坐标中的姿态预测 $y^{\ast }$ 可以被这样得到：

$$y^{\ast }=N-1(\psi (N(x);\theta ))\text{\hspace{1em}(2)}$$

尽管这个式子很简单，但该方法的功效和复杂性是 $\psi$ 决定的，它基于卷积深度神经网络（DNN）。这种卷积网络由几个层组成——每个层都是线性变换，但最后一层是非线性变换。第一层将预定义大小的图像作为输入，并且其大小等于三个颜色通道乘以像素数。最后一层输出回归的目标值，在作者的例子中是 $2k$ 个坐标。

作者将 $\psi$ 的结构建立在Krizhevsky等人[14] 用于图像分类的工作基础之上。它在目标定位方面也显示出优异的结果[23]。简而言之，该网络由7层组成（见 图2左 ）。 $C$ 表示卷积层， $LRN$ 表示局部响应归一化层， $P$ 表示池化层， $F$ 表示完全连接层。只有 $C$ 和 $F$ 层包含可学习的参数，而其余的参数是自由的。 $C$ 和 $F$ 层都包括线性变换，并且在线性变换后是非线性变换，在作者的例子中的非线性变换是整流线性单元。对于 $C$ 层，它的大小定义为宽度×高度×深度，其中前两个维度具有空间含义，而深度是滤波器的数量。如果作者在括号中写出每层的大小，那么可以简洁地描述网络： $C(55\ast 55\ast 96)-LRN-P-C(27\ast 27\ast 256)-LRN-P-C(13\ast 13\ast 384)-C(13\ast 13\ast 384)-C(13\ast 13\ast 256)-P-F(4096)-F(4096)$ 。滤波器前两个 $C$ 层的尺寸为11×11和5×5，其余三个为3×3。在三层之后应用池化，尽管分辨率降低，但仍有助于提高性能。网络的输入是220×220的图像，通过4的步幅被馈送到网络中。模型中的参数总数约为40M。有关详细信息，请参[14]。

通用DNN架构的使用受到其在分类和定位问题上的出色结果的推动。在实验部分中，作者展示了这种通用架构可用于学习模型，从而在姿态估计方面产生最新技术或更好的性能。此外，这样的模型是真正的整体模型——最终的关节位置估计基于完整图像的复杂非线性变换。

另外，DNN的使用消除了设计特定域的姿态模型的需要，而是从数据中学习这样的模型和特征。虽然回归损失不能模拟关节之间的显式交互，但是所有7个隐藏层都隐含地捕获了这些关系——所有内部特征都由所有联合回归分享。

训练 本文的与[14]的差异是损失。与分类损失不同的是，作者训练线性回归的最后一个网络层，通过最小化预测和真实姿态向量之间的 $L_2$ 距离来预测姿态向量。由于ground truth的姿态向量是在绝对图像坐标中定义的，并且姿态在图像之间大小不同，因此作者使用来自公式(1)的归一化来标准化作者的训练集:

$$D_N=(N(x),N(y))|(x,y)\in D\text{\hspace{1em}(3)}$$

然后，用于获得最佳网络参数的 L2 损失：

$$\arg \min \sum _{(x,y)\in D_N}\sum _{i=1}^k||y_i-{\psi }_i(x;\theta )|{|}_2^2\text{\hspace{1em}(4)}$$

为清楚起见，作者写出了对各个关节的优化。应该注意，即使对于某些图像并非所有关节都被标记，也可以使用上述目的。在这种情况下，将省略总和中的相应项。

上述参数 $\theta$ 针对在分布式在线实现中使用反向传播进行了优化。对于尺寸为128的每个小批，计算自适应梯度更新[3]学习率作为最重要的参数，设置为0.0005。由于模型具有大量参数且使用的数据集的大小相对较小，因此作者使用大量随机翻译的图像裁剪来增加数据（参见3.2章），左/右翻转以及 $F$ 层的DropOut正则化设置为0.6。

3.2 级联姿态回归器

来自前一部分的姿态公式具有以下优点：联合估计基于完整图像并因此依赖于上下文。然而，由于其固定输入大小为220×220，网络查看细节的能力有限——它学习的滤波器以粗略的比例捕获姿态属性。这些粗糙姿态的估计是必要的，但不足以始终精确地定位身体关节。值得注意的是，不能轻易增加输入大小，因为这样将增加已经很多的参数。为了获得更好的精度，作者建议训练一系列姿态回归量。在第一阶段，级联通过估计初始姿态开始，如上一节所述。在后续阶段，训练额外的DNN回归器以预测从前一阶段到真实位置的关节位置的位移。因此，每个后续阶段可以被认为是当前预测姿态的细化，如 图4 所示。

此外，每个后续阶段使用预测的关节位置来聚焦在图像的相关部分上——子图像在前一阶段的预测关节位置周围被裁剪，并且该关节的姿态位移回归量被应用于该子图像。通过这种方式，随后的姿态回归器可以得到更高分辨率的图像，从而学习更精细尺度的特征，从而最终实现更高的精度。

作者对级联的所有阶段使用相同的网络架构，但学习不同的网络参数。对于阶段 $s\in \{1,...,S\}$ ，共S个级联阶段，作者用 ${\theta }_s$ 表示学习的网络参数。因此，姿态位移回归量是 $\psi (x;{\theta }_s)$ 。给定关节位置 $y_i$ ，计算一个关节边界框 $b_i$ ，以捕获 $y_i$ 周围的子图像：$b_i(y;\sigma )=(y_i,diam(y)\sigma ,diam(y)\sigma )$ 以第 $i$ 个坐标作为中心，并且尺度为 $\sigma$ 。姿态的直径 $diam(y)$ 定义为人体躯干上关节之间的相对距离，例如左肩和右臀，并取决于具体的姿态定义和数据集。

使用上述表示法，在阶段 $s=1$ 时，作者从边界框 $b^0$ 开始，该边界框 $b^0$ 包围整个图像或由人检测器获得。这样作者获得了一个初步姿态：

$$Stage1:y^1\leftarrow N^{-1}(\psi (N(x;b^0);{\theta }_1);b^0)\text{\hspace{1em}(5)}$$

在每个后续阶段 $s\ge 2$ ，对于所有关节 $i\in \{1,...,k\}$ 作者通过在子图像上应用回归来精细化位置 $y_i^s-y_i^{(s-1)}$ 。子图像由来自之前 $(s-1)$ 层的 $b_i^{(s-1)}$ 定义。然后，作者重新估计方框 $b_i^s$ ：

$$Stage2:y_i^s\leftarrow N_i^{-1}({\psi }_i(N(x;b);{\theta }_s);b)forb=b_i^{(s-1)}\text{\hspace{1em}(6)}$$

$$b_i^s\leftarrow (y_i^s,diam(y^s)\sigma ,diam(y^s)\sigma )\text{\hspace{1em}(7)}$$

作者将级联应用于S个阶段，如4.1所述。

训练 网络参数 ${\theta }_1$ 按照第3.1节中的公式(4)训练。在随后 $s\ge 2$ 的阶段，训练完成相同的微分。来自训练样本 $(x,y)$ 的每个关节 $i$ 使用不同的边界框 $(y(s-1),diam(y^{(s-1)})\sigma ,diam(y^{(s-1)})\sigma )$ 来标准化——这个边界框是从之前的层次中的相同关节为中心——这样作者就可以根据前一阶段的模型来调整阶段的训练。

由于深度学习方法要训练很大的体量，作者通过对每个图像和关节使用multiple normalization来增加训练数据。作者不仅使用前一阶段的预测，而是生成模拟预测。这是通过从二维正态分布 ${\mathcal{N}}_i^{(s-1)}$ 随机抽样的矢量随机移动关节 $i$ 的ground truth位置来完成的，二维正态分布其均值和方差等于观察到的训练数据中的偏置量 $(y_i^{(s-1)}-y_i)$ 相同。被增强的完整训练数据可以这样定义：从均匀的原始数据中采样一个样本和一个关节，然后根据从 ${\mathcal{N}}_i^{(s-1)}$ 的采样的位移 $\delta$ 生成模拟预测：

$$D_A^s=\{(N(x;b),N(y_i;b))|(x,y_i)\sim D,\delta \sim {\mathcal{N}}_i^{(s-1)},b=(y_i+\delta ,diam(y)\sigma )\}$$

级联阶段的训练目标如 公式4 所示，通过特别注意来为每个关节使用正确的标准化：

$${\theta }_s=\arg \underset{\theta }{\min }\sum _{(x,y_i)\in D_A^s}||y_i-{\psi }_i(x;\theta )|{|}_2^2\text{\hspace{1em}(8)}$$

4. 实验评估

4.1. 实验设定

数据集 人体姿态估计有各种各样的基准。在这项工作中，作者使用具有足够的大量训练样本的数据集来训练大型模型，例如所提出的DNN。

使用的第一个数据集是Frames Labeled In Cinema（FLIC）[20]，其中包括来自好莱坞流行电影的4000个训练图像和1000个测试图像。这些图像包含各种姿态的人和各种各样的服装。对于每个标记的人，标记了10个上身关节。

第二个数据集是Leeds Sports Dataset[12] 及其扩展[13]，作者将通过LSP联合表示。结合它们包含11000个训练图像和1000个测试图像。这些来自体育活动的图像在外观特别是关节方面都非常具有挑战性。此外，大多数人具有150像素高度，这使得姿态估计更具挑战性。在该数据集中，对于每个人，全身总共标记有14个关节。

对于所有上述数据集，作者将姿态 $y$ 的直径定义为肩部和臀部之间的距离对立面并用 $diam(y)$ 表示。应该注意的是，所有数据集中的关节都排列在运动学上模仿人体的树中。这允许将肢体定义为姿态树中的一对相邻关节。

度量标准 为了能够与已发布的结果进行比较，作者将使用两个广泛接受的评估度量标准。正确部位（PCP）的百分比用于测量肢体的检测率，如果两个预测的关节位置与真实肢体关节位置之间的距离大于肢体长度的一半，则认为检测到肢体[5]。PCP是最初优选的评估指标，但它具有难以检测较短肢体的缺点，例如较低的手臂通常较难检测。

为了解决这个缺点，最近关于关节的检测率使用不同的检测标准——如果预测关节和真实关节之间的距离在躯干直径的特定部分内，则认为检测到关节。通过改变该分数，获得不同程度的定位精度的检测率。该度量减轻了PCP的缺点，因为所有关节的检测标准都基于相同的距离阈值。作者将此度量标准称为检测到的关节百分比（PDJ）。

实验细节 对于所有实验，作者使用相同的网络架构。作者在FLIC上使用身体探测器来初步获得人体边界框的粗略估计，这种灵感来自[7]。它基于面部检测器——检测到的面部矩形由固定的缩放器放大。该缩放器根据训练数据确定，使得它包含所有标记的关节。这种基于面部的身体检测器可以进行粗略估计，但这为作者的方法提供了一个很好的起点。对于LSP，作者使用完整图像作为初始边界框，因为人类在设计上相对紧密地裁剪。

对每个数据集使用一组50个的小图像来确定算法超参数。为了测量参数的最优性，所使用PDJ的平均值超过所有关节0.2。缩放器 $\sigma$ 被定义为精化关节边界框的大小，作为姿态大小的一部分：对于FLIC，作者在探索值0.8、1.0、1.2之后选择 $\sigma =1.0$ ，对于LSP作者尝试1.5、1.7、2.0、2.3后使用 $\sigma =2.0$ 。级联级数 S 由训练阶段确定，直到算法停止改进为止。对于FLIC和LSP，作者令 $S=3$ 。

为了改进泛化，对于从 $s=2$ 开始的每个级联阶段，作者通过对每个关节抽样40个随机变换过的裁剪框来增加训练数据，如 3.2节 中所述。因此，对于具有14个关节的LSP并且在对镜像进行镜像并对数量进行采样后，训练样本数目为11000×40×2×14=12M，这对于训练大型网络是必要的。

所提出的算法可以进行有效的实现。在12核CPU上测量，运行时间约为每个图像0.1秒。这与其他方法相比是有利的，因为一些当前最先进的方法具有更高的复杂性：[20] 约4秒，[27] 在1.5秒内运行。本算法的训练的复杂性更高。初始阶段消耗大约3天去训练。大部分最终表现是在12小时后完成的。每个细化阶段都训练了7天，因为数据量比初始阶段的数据大40被，这是由于3.2章中的数据增加造成的。以后使用更多数据可以提高性能。

4.2 结果与讨论

比较 作者将结果与其他方法进行比较。作者在 图1 中使用PCP度量在LSP数据集上进行比较。作者显示了四个最具挑战性的结果——下臂和上臂和腿——以及所有比较算法的平均值。作者明显优于所有其他方法，特别是实现更好的腿部估计。例如，对于上腿，作者从0.74优化到了0.78。值得注意的是，虽然其他方法对特定肢体表现出优势，但其他数据集都不能始终支配所有肢体。相反，DeepPose对所有具有挑战性的肢体都表现出强烈的效果。

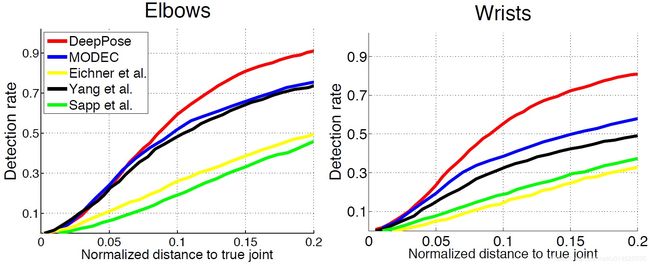
图3 FLIC上检测到的关节肘部和腕部的百分比（PDJ）：将两个级联阶段后的DeepPose与其他四种方法进行比较。

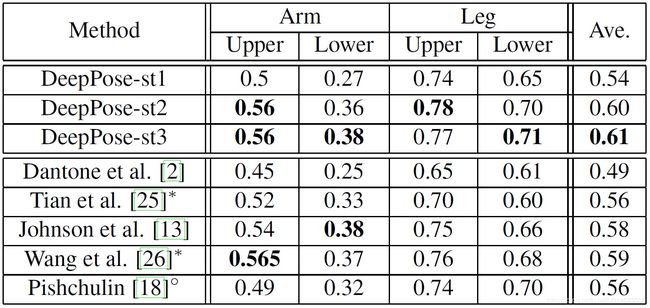
表1 用于Deep-Pose的LSP上的正确部分（PCP）的百分比为0.5，以及与五种最先进的方法的比较。作者使用稍微宽松的PCP版本，用每个肢体的平均值与预测肢体关节的距离用于确定是否正确检测到肢体。作者使用以人为中心的表示。

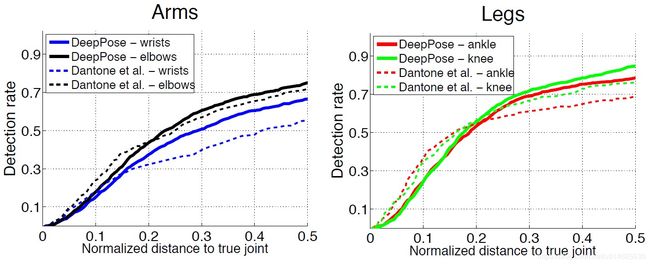
图4 DeepPose和Dantone等人[2]在四肢的LSP上检测到的关节（PDJ）的百分比。在距离真实关节的较大距离范围内——躯干直径的[0,0.5]。DeepPose的结果用实线绘制，而所有结果用[2]以虚线绘制。来自两种算法的相同关节的结果用相同颜色着色。

作者使用PDJ度量时改变预测和ground truth之间的距离的阈值。该阈值可以被认为是显示检测率的定位精度。因此，可以比较不同期望精度的方法。作者在 图3 显示FLIC数据集的实验结果。另外四种方法在LSP数据集的比较也在 图4 中显示。作者根据每个数据集进行训练和测试。与之前的实验类似，作者方法优于所有五种已有算法。在检测粗糙姿态而不精确定位关节的情况下，作者在低精度域中的增益更大。在FLIC上，当归一化距离为0.2时，肘部和腕部的检测率增加了0.15和0.2。在LSP上，在归一化距离为0.5时，作者得到实验结果增加了0.1。在LSP的标准化距离为0.2的低精度状态下，在腿部检测上的性能比较好，但在胳膊检测上的效果稍差。这可以归因于这样一个事实，即基于DNN的方法使用7层变换计算联合坐标，其中一些变换包含max pooling层。另一个事实是作者的方法适用于电影数据以及线连接的数据，例如LSP中的体育图像。

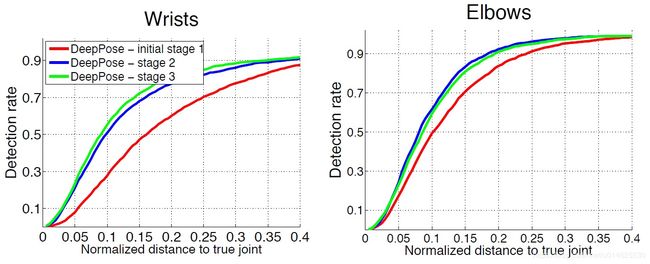
图5 FLIC上检测到的关节（PDJ）或DNN级联的前三个阶段的百分比。在更大范围的预测和ground truth之间归一化距离上呈现结果。

图6 三级级联网络预测姿态为红色和地面ground truth的姿态为绿色。

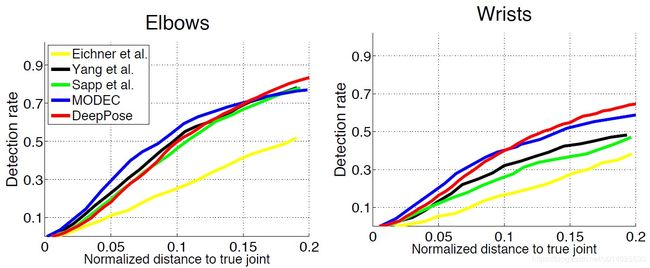
图7 Buffy数据集上检测到两个关节的关节（PDJ）的百分比：肘部和手腕。这些模型已经在FLIC上接受过训练。将两个级联阶段后的DeepPose与其他四种方法进行比较。

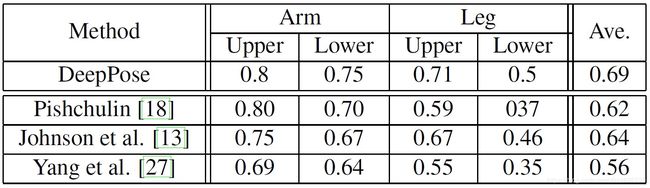
表2 DeepPose的Image Parse数据集上的0.5的正确部分（PCP）的百分比以及Image Parse数据集上的两种最先进的方法[18]获得的结果。

基于级联细化的影响 单个基于DNN的关节回归器给出了粗糙的关节位置。然而，为了获得更高的精度，级联的后续阶段（其作为初始预测的改进）是至关重要的。 图5 中作者提出了不同精度的检测，用于初始预测以及随后的两个级联阶段。正如预期的那样，作者可以看到细化的主要收获是在标准化距离为[0.15,0.2]的高精度方案。此外，经过一个细化阶段后，主要的增益得以实现。原因是后续阶段最终在每个关节周围使用较小的子图像。虽然随后的层看起来更高分辨率的输入，但他们使用的背景更有限。

优化的帮助在图6中可视化。初始阶段通常在估计大致正确的姿态时是成功的，但是，这不会“捕捉”到正确的姿态。例如，在第三行中，姿态具有正确的形状但是不正确的比例。在第二行中，预测的姿态从理想状态向北移动。在大多数情况下，级联的第二阶段解决这个对齐问题，以更好地对齐关节。在更罕见的情况下，例如在第一行中，进一步的阶段改善了各个关节的检测效果。

跨数据集泛化 为了评估算法的泛化属性，作者在两个相关数据集上使用LSP和FLIC上的训练模型。在LSP上训练的全人模型在Image Parse数据集[19] 的测试部分上进行测试，结果列于表中2。ImageParse数据集类似于LSP，因为它包含进行体育运动的人，但它包含许多来自其他活动的个人照片集的人。此外，将在FLIC上训练的上身模型应用于整个Buffy数据集[7]。作者可以看到作者的与其他方法相比，该方法可以保持最好的性能。这显示了良好的泛化能力。为了能更好地展示作者的算法的性能，作者在 图8 中可视化来自LSP的图像上的姿态估计样本。可以看到作者的算法能够在各种条件下获得大多数关节的正确姿态：颠倒的人（第1行，第1列），严重的缩短（第1行，第3列），不寻常的姿态（第3行，列5），第3行、第2列、第6列中的遮挡的手臂和遮挡的肢体，以及不寻常的照明条件（第3行，第3列）。在大多数情况下，当估计的姿态是不精确，它仍然具有正确的形状。例如，在最后一行中，一些预测肢体未与真实位置对齐，但是姿态的整体形状是正确的。当从后面拍摄人物时，常见的故障模式会使左右混淆（第6行，第6列）。FLIC的结果（见 图9 ) 中下臂偶尔会出现明显错误。

图8 来自LSP的图像的姿态结果的可视化。每个姿态都表示为一个从预测的关节推断出来的简笔画。同一图像中的不同肢体被不同地着色，不同图像上的相同肢体具有相同的颜色。

图9 来自FLIC的图像的姿态结果的可视化。图例的含义与 图1 中的相同。

5. 结论

作者提出了深度神经网络（DNN）在人体姿态估计中的首次应用，将问题表述为基于DNN的回归到关节坐标。所呈现的这种回归的级联具有以整体方式捕获关于姿态的背景和推理的优点。因此，作者能够在几个具有挑战性的学术数据集上实现最先进或更好的结果。

此外，作者展示了使用通用卷积神经网络的方法，该网络最初是为分类设计的任务，可以应用于不同的本地化任务。将来，作者计划研究新颖的架构，这些架构可能更适合一般的定位问题，尤其是姿态估计。

致谢

作者要感谢Luca Bertelli，Ben Sapp和Tianli Yu对数据和成果的帮助

参考文献

[1] M. Andriluka, S. Roth, and B. Schiele. Pictorial structures revisited: People detection and articulated pose estimation. In CVPR, 2009.
[2] M. Dantone, J. Gall, C. Leistner, and L. Van Gool. Human pose estimation using body parts dependent joint regressors. In CVPR, 2013.
[3] J. Duchi, E. Hazan, and Y. Singer. Adaptive subgradient methods for online learning and stochastic optimization. In
COLT. ACL, 2010.
[4] M. Eichner and V. Ferrari. Better appearance models for pictorial structures. 2009.
[5] M. Eichner, M. Marin-Jimenez, A. Zisserman, and V. Ferrari. Articulated human pose estimation and search in (almost) unconstrained still images. ETH Zurich, D-ITET, BIWI, Technical Report No, 272, 2010.
[6] P. F. Felzenszwalb and D. P. Huttenlocher. Pictorial structures for object recognition. International Journal of Computer Vision, 61(1):55–79, 2005.
[7] V. Ferrari, M. Marin-Jimenez, and A. Zisserman. Progressive search space reduction for human pose estimation. In CVPR, 2008.
[8] M. A. Fischler and R. A. Elschlager. The representation and matching of pictorial structures. Computers, IEEE Transactions on, 100(1):67–92, 1973.
[9] R. Girshick, J. Donahue, T. Darrell, and J. Malik. Rich feature hierarchies for accurate object detection and semantic segmentation. In CVPR, 2014.
[10] G. Gkioxari, P. Arbel´aez, L. Bourdev, and J. Malik. Articulated pose estimation using discriminative armlet classifiers. In CVPR, 2013.
[11] C. Ionescu, F. Li, and C. Sminchisescu. Latent structured models for human pose estimation. In ICCV, 2011.
[12] S. Johnson and M. Everingham. Clustered pose and nonlinear appearance models for human pose estimation. In BMVC, 2010.
[13] S. Johnson and M. Everingham. Learning effective human pose estimation from inaccurate annotation. In CVPR, 2011.
[14] A. Krizhevsky, I. Sutskever, and G. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012.
[15] G. Mori and J. Malik. Estimating human body configurations using shape context matching. In ECCV, 2002.
[16] R. Nevatia and T. O. Binford. Description and recognition of curved objects. Artificial Intelligence, 8(1):77–98, 1977.
[17] M. Osadchy, Y. LeCun, and M. L. Miller. Synergistic face detection and pose estimation with energy-based models. The Journal of Machine Learning Research, 8:1197–1215, 2007.
[18] L. Pishchulin, M. Andriluka, P. Gehler, and B. Schiele. Poselet conditioned pictorial structures. In CVPR, 2013.
[19] D. Ramanan. Learning to parse images of articulated bodies. In NIPS, 2006.
[20] B. Sapp and B. Taskar. Modec: Multimodal decomposable models for human pose estimation. In CVPR, 2013.
[21] G. Shakhnarovich, P. Viola, and T. Darrell. Fast pose estimation with parameter-sensitive hashing. In CVPR, 2003.
[22] Y. Sun, X. Wang, and X. Tang. Deep convolutional network cascade for facial point detection. In Computer Vision and Pattern Recognition (CVPR), 2013 IEEE Conference on, pages 3476–3483. IEEE, 2013.
[23] C. Szegedy, A. Toshev, and D. Erhan. Object detection via deep neural networks. In NIPS 26, 2013.
[24] G. W. Taylor, R. Fergus, G. Williams, I. Spiro, and C. Bregler. Pose-sensitive embedding by nonlinear nca regression. In NIPS, 2010.
[25] Y. Tian, C. L. Zitnick, and S. G. Narasimhan. Exploring the spatial hierarchy of mixture models for human pose estimation. In ECCV, 2012.
[26] F.Wang and Y. Li. Beyond physical connections: Tree models in human pose estimation. In CVPR, 2013.
[27] Y. Yang and D. Ramanan. Articulated pose estimation with flexible mixtures-of-parts. In CVPR, 2011.