B-spline Curves 学习之B样条曲线定义（4）

转自：http://www.cnblogs.com/icmzn/p/5100789.html

　　给定 n + 1个控制点P₀, P₁, ..., P_n 和一个节点向量U = { u₀, u₁, ..., u_m },  p 次B-样条曲线由这些控制点和节点向量U 定义

　　

　　其中 N_i,p(u)是 p次B-样条基函数。 

　　B-样条曲线形式与贝塞尔曲线相似 。不像贝塞尔曲线, B-样条曲线包含更多信息，即：一系列的 n+1 个控制点， m+1个节点的节点向量，次数 p。 注意n, m 和 p 必须满足m = n + p + 1。更准确地，如果我们想要定义一个有 n + 1控制点的p次B-样条曲线，我们必须提供n + p + 2 个节点 u₀, u₁, ..., u_n+p+1。另一方面，如果给出了一个m + 1 个节点的节点向量和n + 1 控制点，B-样条曲线的次数是p = m - n - 1。对应于一个节点u_i的曲线上的点， C(u_i)，被称为节点点（knot point）。因此，节点点把B-样条曲线划分成曲线段，每个都定义在一个节点区间上。我们将在曲线细分页证明这些曲线段都是 p 次的贝塞尔曲线。

　　尽管 N_i,p(u) 看起来像B_n,i(u)， B-样条基函数的次数(degree)是一个输入数，而贝塞尔基函数的次数取决于控制点的数目。

　　为了改变B-样条曲线的形状，可以修改一个或多个控制参数：控制点的位置(n+1)，节点位置(m+1)，和曲线的次数p。

　　如果节点向量没有任何特别的结构，那么产生的曲线不会与控制折线（polyline）的第一边（leg）和最后一边（leg）接触，如下面左图所示。这种类型的B-样条曲线称为开（open ）B-样条曲线。 我们可能想强制曲线使得它分别与第一个控制点和最后一个控制点的第一边和最后一边相切，像贝塞尔曲线那样。为了做到这些，第一个节点和最后一个节点必须是重复度为p+1。这就产生了所谓的clamped B-样条曲线。参见下边中间的图。通过重复某些节点和控制点，产生的曲线会是  闭（closed）曲线。  这种情况，产生的曲线的开始和结尾连接在一起形成了一个闭环如下边右图所示。在本文中，我们将使用clamped曲线。

　　

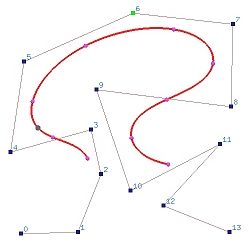
　　上图有 n+1个控制点(n=9)以及 p = 3. 。那么，, m 必须是13 所以节点向量有14个节点。为了有clamped效果，前p+1 = 4 和最后4个节点必须一样。其余14 - (4 + 4) = 6 个节点可在定义域任何位置。实际上，曲线是用节点向量 U = { 0, 0, 0, 0, 0.14, 0.28, 0.42, 0.57, 0.71, 0.85, 1, 1, 1, 1 }产生的。注意除了头四个和最后四个节点，中间的节点几乎是均匀分布的。 图形也显示了每个节点区间上的相应的曲线段。实际上，小三角是节点点。

---

 

术语的使用

我们使用开（open）， clamped 和闭（closed）来描述三种类型的B-样条曲线。但是，不是每一个作者都会使用相同的术语，并没有一个标准用法的共识。例如，有些作者会使用 floating, open 和 periodic 来称呼 开（open）, clamped 和 闭（closed）曲线。其他有些作者会使用"periodic"来称呼一个有均匀节点序列的开（open）B-样条曲线。因此，当你读其他文献时，首先要看其定义。否则，你很可能会感到困惑。

---

B-spline Curves: Open Curves

　　如以前提到过的，如果第一个和最后一个节点没有重复度 p+1，其中 p 是B-样条曲线的次数（degree），曲线将不会分别与第一个控制点和最后一个控制点的第一边和最后一边相切。 该曲线是开（open） B-样条曲线。在这种情况下，我们应关注一个额外的限制。在前页 我们展示了一个基函数的计算实例，使用节点向量U = { 0, 0.25, 0.5, 0.75, 1 }, 其中 m = 4，如果基函数是1次的  (即， p = 1), 那么有三个基函数N_0,1(u), N_1,1(u) 和 N_2,1(u) 如下图所示。

　　

　　因为该节点向量不是 clamped,第一个和最后一个节点区间(即，[0, 0.25) 和 [0.75, 1)) 只有一个非零基函数而第二和第三节点区间(即， [0.25, 0.5) 和 [0.5, 0.75)) 有两个非零基函数。回忆 B-样条基函数重要性质里的在一个节点区间[u_i, u_i+1)有至多p+1个p 次非零基函数。因此，在这个例子中，节点区间[0,0.25) 和 [0.75,1)没有基函数的“完全支持” （"full support"）。一般来说，对次数p，区间 [u₀, u_p) 和 [u_m-p, u_m] 不会有基函数的“完全支持”（ "full support" ），当B-样条曲线是开曲线时被忽略。因此，我们有下列重要的注意事项：

　　

　　考虑一个由14个控制点（即，n = 13)定义的 6次 (即，p = 6) B-样条曲线。其节点的数目是 21 (即， m = n + p + 1 = 20)。如果节点向量是均匀的, 节点是0, 0.05, 0.10, 0.15, ..., 0.90, 0.95 和 1.0。 开（open）曲线定义在[u_p, u_n-p] = [u₆, u₁₄] = [0.3, 0.7]上且与第一边和最后一边不相切。下面左图显示了曲线而右图给出了B-样条基函数。

　　　　

　　尽管在两端的节点区间没有被利用，B-样条曲线仍然是由所有控制点定义的。如在 B-样条基函数页所讨论的最多有p+1 个基函数N_i-p,p(u), N_i-p,p+1(u), ..., N_i,p(u) 在节点区间 [u_i, u_i+1)上非零。因此，在[u_p, u_i+1)上有 p+1个非零函数： N_0,p(u), N_1,p(u), ..., N_p,p(u)。这是一个“满”数（ "full" count）。注意 N_0,p(u) 在 [u_p, u_p+1) 有它的尾巴，因此，控制点P₀ 对开（open）B-样条曲线的贡献小于大多数其他控制点。一个相似的参数可用来证明 P_n 也包括在曲线的定义中。

　　让我们用一个实例来说明一个开曲线与clamped曲线之间的变化。 我们以一个由9个控制点(即， n = 8)和一个均匀节点向量{ 0, 1/13, 2/13, 3/13, ..., 12/13, 1 }定义的4次开B-样条曲线为开始。如果我们将第二个节点 1/13 改变到 0 使得0 为双重节点,图中黄色曲线。实际上，该曲线和0是简单节点的原始曲线几乎是一样的。现在，如果我们把第三个节点2/13改变到0使得0是重复度为3的节点，则结果是红色曲线。如果第四个节点 3/13 改变到0 (重复度 4),产生的曲线是蓝色的。如你所看到的，这三条开曲线彼此之间没有很大不同。现在，让我们把第五个节点4/13改变到0. 现在0是一个重复度5(即， p+1)的节点，曲线不仅通过第一个控制点而且与控制折线（ployline）（即，clamped）的第一边相切。如你从图中看到的，曲线的形状剧烈地变化，将它的一个端点移到第一个控制点。如果我们把最后5个节点移到1也会发生同样变化。

　　

 

---

 B-spline Curves: Closed Curves

　　有许多方法来产生闭曲线。简单的一种就是或者wrapping控制点或者wrapping节点向量。

1.Wrapping控制点

　　假设我们想构建一个p次闭（closed）B-样条曲线C(u)，由n+1 控制点P₀, P₁, ..., P_n.定义。节点数目是m+1, 其中 m = n + p + 1. 这儿是构建过程：

(1)设计一个均匀 m+1 个节点的节点序列：u₀ = 0, u₁ = 1/m, u₁ = 2/m, ..., u_m = 1。注意曲线的定义域是 [u_p, u_n-p].

(2)Wrap头p 个和最后p 个控制点。更准确地，设P₀ = P_n-p+1, P₁ = P_n-p+2, ..., P_p-2 = P_n-1 and P_p-1 = P_n. 如下图所示。

　　构建的曲线在连接点处 C(u_p) = C(u_n-p)是C^p-1 连续的。.

　　下面举个例子图 (a) 显示了一个由10（n=9）个控制点和一个均匀节点向量定义的3次开（open）B-样条曲线。在图中，控制点对0 和7, 1和8, 以及2和9放置在相互靠近的地方来说明这个构建。图 (b) 显示了使得点0和7重叠的结果。 曲线的形状没有太大变化。那么，控制点1和8重叠如图(c)所示。很显然曲线的第一点和最后一点的间距更近了。最后曲线变成一个闭曲线当控制点2和9重叠后，如图(d)所示。

　　

　　

（2）Wrapping 节点

　　另一种构建闭B-样条曲线的方法是wrapping节点。假设我们想要构建一个由n+1个控制点P₀, P₁, ..., P_n定义的p 次闭B-样条曲线C(u) 。构建过程如下：

（1）增加一个新控制点 P_n+1 = P₀.因此，控制点的数目是 n+2.

（2）找到一个合适的有 n+1节点的节点序列u₀, u₁, ..., u_n 。这些节点不必要是均匀的

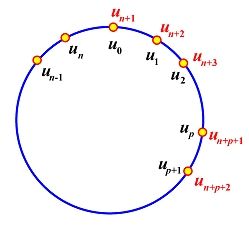
（3）增加 p+2 个节点并 wrap 头 p+2个节点： u_n+1 = u₀, u_n+2 = u₁, ..., u_n+p = u_p-1, u_n+p+1 = u_p, u_n+p+2 = u_p+1 ，如下图所示。这样，我们有n+p+2 = (n+1) + p + 1 个节点

（4）定义在上述构建的 n+1个控制点和n+p+2 个节点上的 p 次开B-样条曲线C(u)是一个闭曲线，在连接点处C(u0) = C(un+1)有Cp-1 连续性。注意闭曲线的定义域是 [u₀, u_n+1]