《数字图像处理(第三版)》 第三章 数字图像处理 笔记2 (基本的灰度变换函数)
第 3 章 灰度变换与空间滤波
3.2 一些基本的灰度变换函数
灰度变换是所有图像处理技术中最简单的技术,涉及
s = T ( r ) s = T(r) s=T(r)
其中 T 是把像素值 r 映射到像素值 s 的一种变换。
由于处理的是数字量,变换函数的值通常存储在一个一维阵列中,并且从 r 到 s 的映射通过查表得到。对于 8 比特环境,一个包含 T 值的可查阅的表需要有 256 个记录。
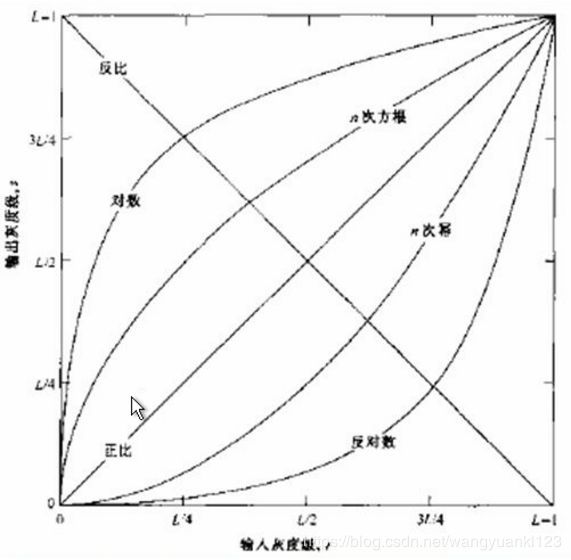
如上图显示了图像增强常用的三类基本函数:线性函数(反转和恒等变换)、对数函数(对数和反对数变换)和幂律函数(n 次幂和 n 次根变换)。
3.2.1 图像反转
对于灰度级范围为 [0, L-1] 的一幅图像,该图像的反转由下式给出:
s = L − 1 − r s = L - 1 - r s=L−1−r
使用这种方式反转一幅图像的灰度级,可得到等效的照片底片。这种类型的处理特别适用于 增强嵌入图像暗色区域中的白色或灰色细节,特别是 当黑色面积在尺寸上占主导地位时。
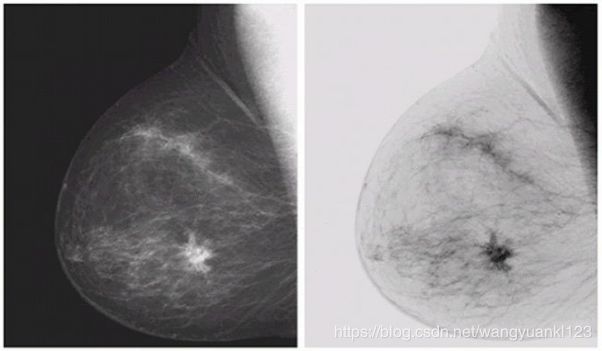
如下例子中原图像(左图)是一幅数字乳房 X 射线照片,其中显示有一小块病变。通过反转得到右图,尽管视觉内容上都一样,但反转之后的图像在分析乳房组织时会更加容易。
3.2.2 对数变换
通用形式为:
s = c ∗ l o g ( 1 + r ) s = c * log(1 + r) s=c∗log(1+r)
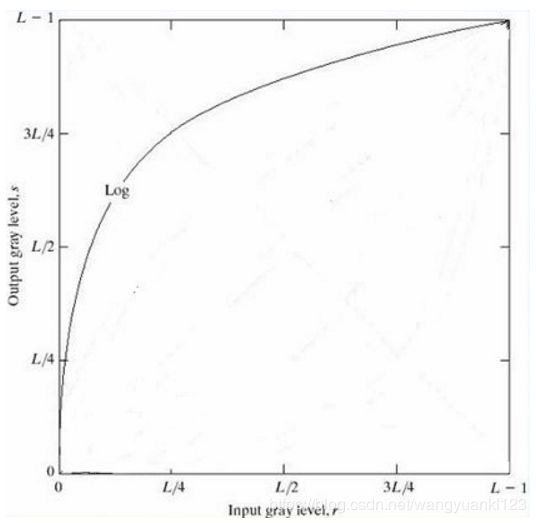
式中 c 是常数,并假设 r>=0。如下图所示:
此变换将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度值,或将输入中范围较宽的高灰度值映射为输出中范围较窄的灰度值。使用这种类型的变换来 扩展图像中的暗像素值,同时压缩更高灰度级的值。反对数变换的作用与此相反。
对数变换中对数的底数可以有多种选择,以 2、10、e 为底均可。
具有对数函数一般形状的任何曲线,都能完成图像灰度级的扩展/压缩,但后面将要讨论的幂律变换更适用于这儿目的。
如果原图像的灰度级为 L,对数变换公式的结果应当重新标定为 [0, L-1] 的灰度级。例如,对于一幅 256 灰度级的原图像,对数变换增强的结果可用以下式子表示
s = c ∗ l o g ( 1 + r ) − c ∗ l o g ( 1 + 0 ) c ∗ l o g ( 1 + 255 ) − c ∗ l o g ( 1 + 0 ) ∗ 255 s = \frac{c * log(1+r) - c * log(1+0)}{c * log(1+255) - c * log(1+0)} * 255 s=c∗log(1+255)−c∗log(1+0)c∗log(1+r)−c∗log(1+0)∗255
对数函数有一个重要特征,即它 压缩像素值变化较大的图像的动态范围。像素值有较大动态范围的一个典型应用说明是 傅里叶频谱。通常,频谱值的范围从 0 到 106 或更高的情况是常见的,如果采用均匀量化,最后的效果是有很多的细节会在典型的傅里叶频谱显示是丢失。
如下图示例中,左图为原始的傅里叶频谱,值域为 0 ~ 1.5 × 106 ,当这些值在一个 8 比特系统中被线性地缩放显示时,最亮的像素将支配该显示,频谱中地低值(恰恰是重要的)将损失掉。通过对数变换,将值域变为 0 ~ 6.2 得到右图,与未改进显示地频谱相比,这幅图像中可见细节地丰富程度很明显。
所以 对数变换最主要的应用是傅里叶频谱的增强。
3.2.3 幂律(伽马)变换
幂律变换的基本形式为
s = c r γ s = cr^\gamma s=crγ
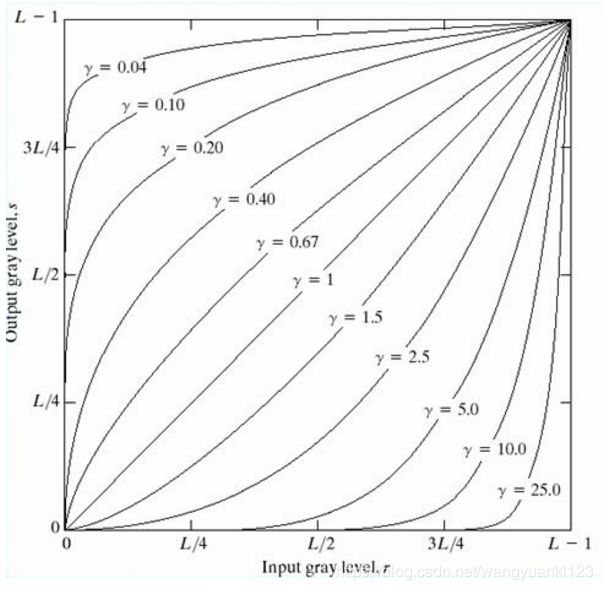
其中 c 和 γ 为正常数。对于不同的 γ 值,s 与 r 的关系曲线如下图所示。与对数变换情况类似,部分 γ 值的幂律曲线将较窄范围的暗色输入值映射为较宽范围的输出值,或将较宽范围的高灰度级输入值映射为较窄范围的输出值。
如上图所示,γ > 1 的值所生成的曲线和 γ < 1 的值所生成的曲线的效果完全相反。当 c = γ = 1 时就简化为了恒等变换。
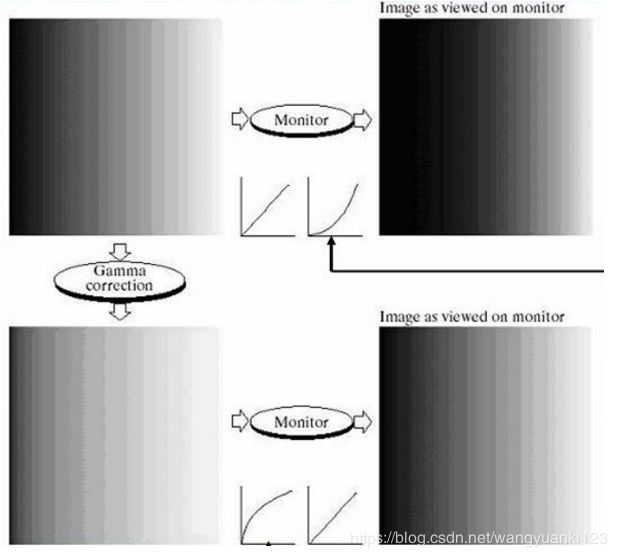
用于图像获取、打印和显示的各种设备根据幂律变换来产生响应。习惯上,幂律方程中的指数称为 伽马。用于校正这些幂律响应现象的处理称为 伽马校正,指用来校正监视器显示的非线性特点。
阴极射线管(CRT)设备有一个灰度——电压响应,该响应是一个指数变化范围约为 1.8 ~ 2.5 的幂函数。如下图示例中,左上图显示了一幅输入到监视器的简单灰度斜坡(渐变)图像。右上图是显示器输出的结果,可以看到,显示器直接输出比输入暗。在这种情况下,伽马校正很简单,只需要将图像输入到监视器前进行预处理,即进行 s = r1/2.5 = r0.4 变换,结果如左下图所示。当输入到相同的监视器时,经过伽马校正的输入产生外观接近于原图像的输出,如右下图所示。类似的分析也适用于其他图像设备,如扫描仪和打印机。
若所关注的是在计算机屏幕上精确显示图像,则伽马校正很重要。试图精确再现彩色也需要伽马校正的一些知识,因为改变伽马值不仅会改变亮度,而且会改变彩色图像中的红、绿、蓝的比率。
此外,目前的图像标准并不包含创建图像的伽马值,因此问题进一步复杂化了。由于这些限制,在网站中存储图像时,一种合理的方法是用伽马值对图像进行预处理,这个伽马值代表了在开放的市场中,在任意给定时间点,各种型号监视器和计算机系统所期望的 “平均值”。
使用幂律变换还能增强对比度,对于原始图像整体偏暗的情况,需要扩展灰度级;对于原始图像偏亮的情况,需要进行灰度级压缩。
下图中,图(a)显示了一幅人体胸上部脊椎骨折和椎线受影响的核磁共振图像。在图中上部约 1/4 处,骨折显而易见,由于所给图像整体为暗色,灰度的扩大是需要的,这可由指数为分数的幂次变换来完成。对图(a)的幂次变换函数处理可以得到示于图中的其他几幅图像。图(b)到(d)相应的伽马值分别为 0.6、0.4 和 0.3。
图(a) 有 “冲淡” 的显示小国,表明灰度级需要压缩,令 c = 1,γ 值大于 1。令 γ = 3.0、4.0 和 5.0 的处理结果示于图(b)到图(d)。可见,伽马值取 3.0 和 4.0 时,可得到合适的结果,且后者由于有较高的对比度而显示出较好的效果。γ = 5.0 得到的结果有些地方太暗,从而丢失了一些细节。
3.2.4 分段线性变换函数
分段线性函数相比前面所讨论函数的主要优势在于它的形式可以任意合成。同时,分段线性函数的主要缺点是其需要更多的用户输入。
下面主要介绍分段线性变换函数的三个应用:
- 对比度拉伸
- 灰度级分层
- 比特平面分层
3.2.4.1 对比度拉伸
最简单的分段线性函数之一是 对比度拉伸变换。低对比度图像由照明不足、成像传感器动态范围太小、图像获取过程中镜头光圈设置错误引起。对比度拉伸是 扩展图像灰度级动态范围的处理,因此可以跨越记录介质和显示装置的全部灰度范围。
下图是对比度拉伸的一个例子:
- 图(a)是对比度拉伸的典型变换,点 (r1, s1) 和 (r2, s2) 的位置控制了变换函数的形状。一般情况下,r1 <= r2,且 s1 <= s2,函数是单值的且单调递增的。这一条件保持了灰度级的次序,从而避免了在处理后的图像中产生人为的灰度错误。
- 图(b)为 8 比特低对比度图像。
- 图©为对比度拉伸的效果,设置 (r1, s1) = (rmin, 0),且 (r2, s2) = (rmax, L-1),其中 rmin,rmax 分别代表图像中灰度的最小值和最大值。若 r1 = r2,s1 = 0,且 s2 = L-1,变换变为阈值处理函数,并产生二值图像。
- 图(d)所示,若 r1 = r2,s1 = 0,且 s2 = L-1,变换变为阈值处理函数,并产生二值图像。
3.2.4.2 灰度级分层
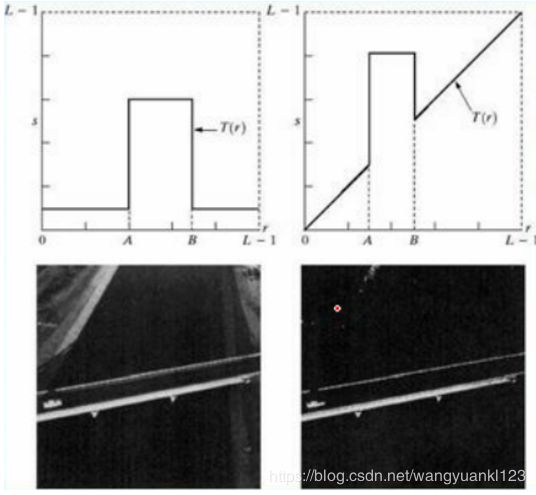
在图像中提高特定灰度范围的亮度通常是必要的,也被称为 灰度级分层,其应用包括增强某些特征。
有许多方法可以进行灰度级分层,但大多数是两种基本方法的变形:
- 一种是将感兴趣范围内的所有灰度值显示为一个 较高值(譬如 “白色” )而将其他灰度值显示为另一个 较低值(譬如 “黑色” ),产生一幅二值图像。
- 第二种方法使所需范围的灰度变亮,但是仍保持了图像的背景和灰度色调。
测试程序
#define CVUI_IMPLEMENTATION
#define CVUI_DISABLE_COMPILATION_NOTICES
#include "cvui.h"
#include (xCoord, yCoord));
cvui::printf(frame, 100, 930, 0.9, 0x000000, "Pixel Value = %d", src.at<uchar>(yCoord, xCoord));
break;
default:
break;
}
cvui::text(frame, 770, 900, "Min Gray Value : ", 0.7, 0x000000);
cvui::trackbar(frame, 970, 890, 500, &minSetGrayValue, (double)0, (double)255, 32, "%.0Lf");
cvui::text(frame, 770, 950, "Max Gray Value : ", 0.7, 0x000000);
cvui::trackbar(frame, 970, 940, 500, &maxSetGrayValue, (double)0, (double)255, 32, "%.0Lf");
if (tempMinSetGrayValue != minSetGrayValue || tempMaxSetGrayValue != maxSetGrayValue)
{
transformForMethod1(src, dst, minSetGrayValue, maxSetGrayValue);
tempMinSetGrayValue = minSetGrayValue;
tempMaxSetGrayValue = maxSetGrayValue;
}
if (cvui::button(frame, 1400, 10, "Exit"))
break;
cvui::imshow("Method 1", frame);
if (cv::waitKey(20) == 27)
break;
}
return;
}
void method2()
{
cv::Mat src = cv::imread(cv::samples::findFile("kidney.tif"), cv::IMREAD_GRAYSCALE);
cv::Mat dst;
dst.create(src.size(), src.type());
cvui::init("Method 2");
cv::Mat frame = cv::Mat(cv::Size(1500, 1000), CV_8UC1);
double minSetGrayValue = 50;
double maxSetGrayValue = 100;
double tempMinSetGrayValue = 0;
double tempMaxSetGrayValue = 0;
while (true)
{
frame = cv::Scalar(255);
cvui::text(frame, 700, 5, "Method 2", 1.3, 0x000000);
cvui::image(frame, 20, 60, src);
cvui::image(frame, 760, 60, dst);
int status = cvui::iarea(20, 60, 720, 828);
int xCoord; int yCoord;
switch (status)
{
case cvui::OVER:
cvui::printf(frame, 100, 900, 0.9, 0x000000, "Pointer Coordinate : (%d, %d)", cvui::mouse().x - 20, cvui::mouse().y - 60);
xCoord = cvui::mouse().x - 20; yCoord = cvui::mouse().y - 60;
//cvui::printf(frame, 100, 930, 0.9, 0x000000, "Pixel Value = %d", src.at(xCoord, yCoord));
cvui::printf(frame, 100, 930, 0.9, 0x000000, "Pixel Value = %d", src.at<uchar>(yCoord, xCoord));
break;
default:
break;
}
cvui::text(frame, 770, 900, "Min Gray Value : ", 0.7, 0x000000);
cvui::trackbar(frame, 970, 890, 500, &minSetGrayValue, (double)0, (double)255, 32, "%.0Lf");
cvui::text(frame, 770, 950, "Max Gray Value : ", 0.7, 0x000000);
cvui::trackbar(frame, 970, 940, 500, &maxSetGrayValue, (double)0, (double)255, 32, "%.0Lf");
if (tempMinSetGrayValue != minSetGrayValue || tempMaxSetGrayValue != maxSetGrayValue)
{
transformForMethod2(src, dst, minSetGrayValue, maxSetGrayValue);
tempMinSetGrayValue = minSetGrayValue;
tempMaxSetGrayValue = maxSetGrayValue;
}
if (cvui::button(frame, 1400, 10, "Exit"))
break;
cvui::imshow("Method 2", frame);
if (cv::waitKey(20) == 27)
break;
}
return;
}
void transformForMethod1(const cv::Mat& src, cv::Mat& dst, double& minSetGrayValue, double& maxSetGrayValue)
{
for (size_t iRow = 0; iRow < src.rows; iRow++)
{
for (size_t iCol = 0; iCol < src.cols; iCol++)
{
if (src.at<uchar>(iRow, iCol) <= int(minSetGrayValue))
dst.at<uchar>(iRow, iCol) = 10;
else if (src.at<uchar>(iRow, iCol) <= int(maxSetGrayValue))
dst.at<uchar>(iRow, iCol) = 200;
else
dst.at<uchar>(iRow, iCol) = 10;
}
}
return;
}
void transformForMethod2(const cv::Mat& src, cv::Mat& dst, double& minSetGrayValue, double& maxSetGrayValue)
{
for (size_t iRow = 0; iRow < src.rows; iRow++)
{
for (size_t iCol = 0; iCol < src.cols; iCol++)
{
if (src.at<uchar>(iRow, iCol) <= int(minSetGrayValue))
dst.at<uchar>(iRow, iCol) = src.at<uchar>(iRow, iCol);
else if (src.at<uchar>(iRow, iCol) <= int(maxSetGrayValue))
dst.at<uchar>(iRow, iCol) = 200;
else
dst.at<uchar>(iRow, iCol) = src.at<uchar>(iRow, iCol);
}
}
return;
}
输出结果
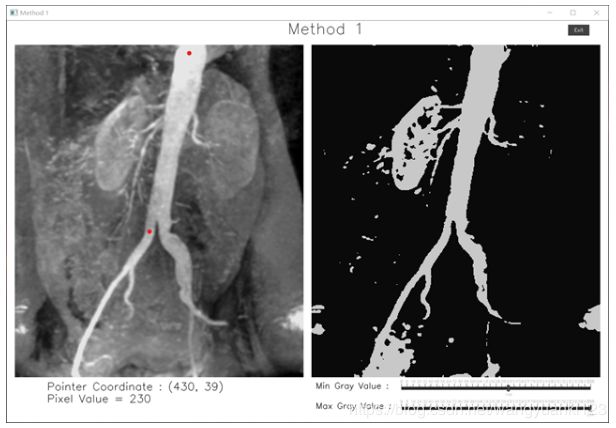
- 方法一
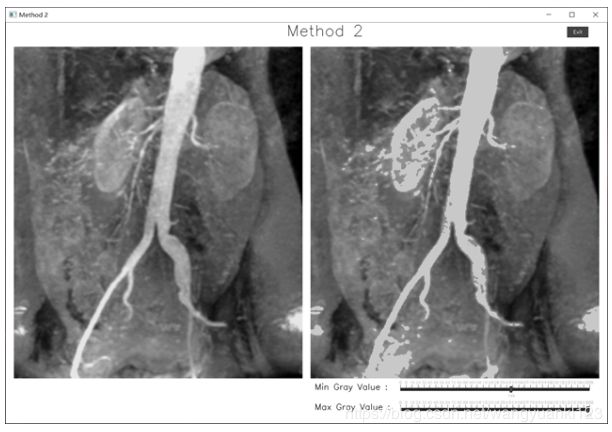
- 方法二
3.2.4.2 比特平面分层
代替提高灰度范围的亮度,通过对特定位提高亮度,对整幅图像质量仍然是有贡献的。
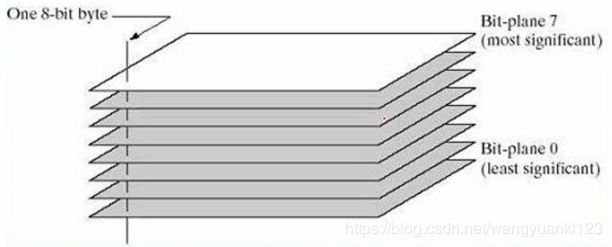
设图像中的每一个像素都是由 8 比特表示,假设图像是由 8 个 1 比特平面组成,其范围从最低有效位的位平面 0 到最高有效位的位平面 7 。在 8 比特字节中,平面 0 包含图像中像素最低位,而平面 7 则包含最高位。即将一幅灰度级为 256 的图像看作是 8 个二值图像。
上图通过比特平面分层可以得到如下所示的 8 张比特平面图。每个比特平面都是一幅二值图像。
把一幅图像分解为比特平面,对于分析图像中每个比特的相对重要性很有用,这一处理可帮助我们确定用于量化该图像的比特数的充分性。此外,这种类型的分解对于图像压缩也很有用,在图像压缩中,重建一幅图像时所用的平面要比全部平面少。在图像重建的实际应用中可以得出如下结论:存储 4 个高阶比特平面将允许我们以可接受的细节来重建福源图像。存储这 4 个平面代替原始图像可减少 50% 的存储量。