** 本文内容来自于吴恩达深度学习公开课
1、概述
加权移动平均法,是对观察值分别给予不同的权数,按不同权数求得移动平均值,并以最后的移动平均值为基础,确定预测值的方法。采用加权移动平均法,是因为观察期的近期观察值对预测值有较大影响,它更能反映近期变化的趋势。
指数移动加权平均法,是指各数值的加权系数随时间呈指数式递减,越靠近当前时刻的数值加权系数就越大。
指数移动加权平均较传统的平均法来说,一是不需要保存过去所有的数值;二是计算量显著减小。
2、算法理解
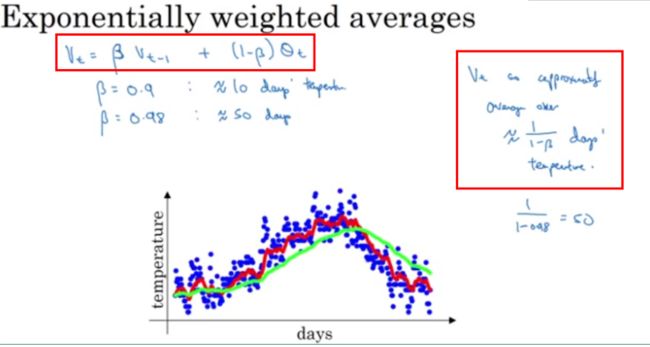
引入一个例子,例子为美国一年内每天的温度分布情况,具体如下图所示
EWMA 的表达式如下:
$v_t = \beta v_{t-1} + (1 - \beta) \theta_t$
上式中 $ \theta_t$ 为时刻 $ t$ 的实际温度;系数 $\beta$ 表示加权下降的速率,其值越小下降的越快;$v_t$ 为 $t$ 时刻 EWMA 的值。
在上图中有两条不同颜色的线,分别对应着不同的 $\beta$ 值。
当 $\beta = 0.9$ 时,有 $v_t = 0.9 v_{t-1} + 0.1 \theta_t$ ,对应着图中的红线,此时虽然曲线有些波动,但总体能拟合真实数据
当 $\beta = 0.98$ 时,有 $v_t = 0.98 v_{t-1} + 0.02 \theta_t$ ,对应着图中的绿线,此时曲线较平,但却有所偏离真实数据
在 $t=0$ 时刻,一般初始化 $v_0 = 0$ ,对 EWMA 的表达式进行归纳可以将 $t$ 时刻的表达式写成:
$ v_t = (1-\beta) (\theta_t + \beta\theta_{t-1}+ ... + \beta^{t-1}\theta_1) $
从上面式子中可以看出,数值的加权系数随着时间呈指数下降。在数学中一般会以 $\frac {1} {e}$ 来作为一个临界值,小于该值的加权系数的值不作考虑,接着来分析上面 $\beta = 0.9 $ 和 $\beta = 0.98$ 的情况。
当 $\beta = 0.9$ 时,$0.9^{10}$ 约等于 $\frac {1} {e}$ ,因此认为此时是近10个数值的加权平均。
当 $\beta = 0.98$ 时,$0.9^{50}$ 约等于 $\frac {1} {e}$,因此认为此时是近50个数值的加权平均。这种情况也正是移动加权平均的来源。
具体的分析如下图所示:
3、偏差修正
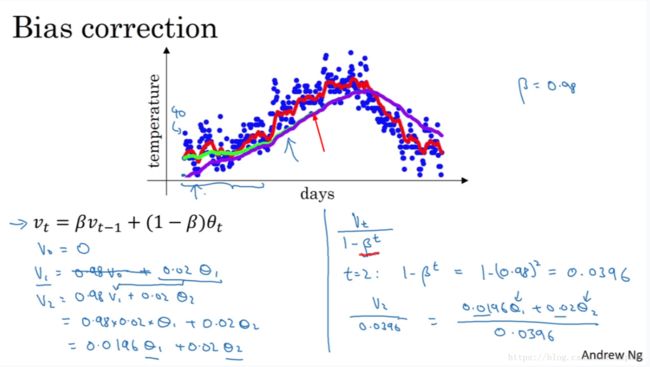
在初始化 $ v_0 = 0$ 时实际上会存在一个问题。具体的如下图所示:
从上图中可以看出有一条绿色和紫色的曲线,都是对应于 $\beta = 0.98$ 时的曲线。理想状况下应该是绿色的曲线,但当初始化 $v_0 = 0$ 时却会得到紫色的曲线,这是因为初始化的值太小,导致初期的数值都偏小,而随着时间的增长,初期的值的影响减小,紫色的曲线就慢慢和绿色的曲线重合。我们对公式做一些修改:
$ v_t = \frac {\beta {v_{t-1}} + {(1 - \beta)} \theta_t} {1 - \beta^t} $
当 $t$ 很小时,分母可以很好的放大当前的数值;当 $t$ 很大时,分母的数值趋于1,对当前数值几乎没有影响。
EWMA 主要是被应用在动量优化算法中,比如Adam算法中的一阶矩和二阶矩都采用了上面修改后的EWMA算法。