什么是神经网络?
在我们开始之前与如何建立一个神经网络,我们需要了解什么第一。
神经网络可能会让人感到恐惧,特别是对于新手机器学习的人来说。但是,本教程将分解神经网络的工作原理,最终您将拥有灵活的神经网络。让我们开始吧!
了解过程
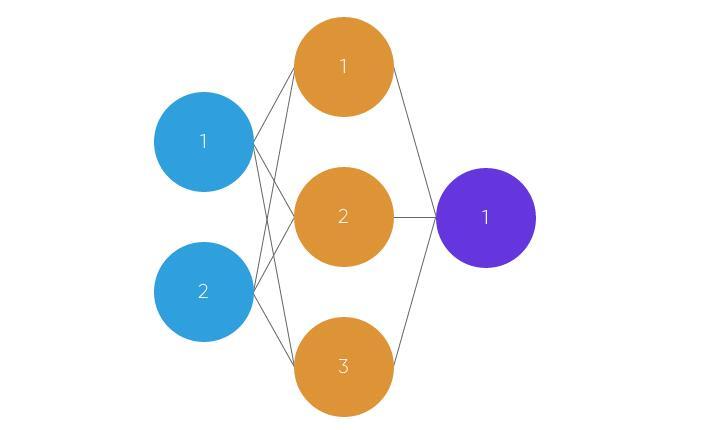
拥有大约100亿个神经元,人类大脑以268英里的速度处理数据!实质上,神经网络是由突触连接的神经元集合。该集合分为三个主要层:输入层,隐藏层和输出层。你可以有许多隐藏层,这就是深度学习这个术语的起源。在人造神经网络中,有几个输入,称为特征,并产生单个输出,称为标签。
圆圈表示神经元,而线条表示突触。突触的作用是将输入和权重相乘。你可以将体重看作神经元之间连接的“强度”。权重主要定义了神经网络的输出。但是,他们非常灵活。之后,应用激活功能返回输出。
以下简要介绍一个简单的前馈神经网络的工作原理:
1.将输入作为矩阵(数字的二维数组)
2.将输入乘以设定权重(执行点积乘以矩阵乘法)
3.应用激活功能
4.返回一个输出
5.通过从数据的期望输出和预测输出的差异来计算误差。这创建了我们的渐变下降,我们可以使用它来改变权重
6.然后根据错误轻微改变权重。
7.为了训练,这个过程重复1000次以上。数据训练得越多,我们的输出结果就越准确。
神经网络的核心是简单的。他们只是使用输入和权重执行点积并应用激活函数。当权重通过损失函数的梯度进行调整时,网络适应变化以产生更准确的输出。
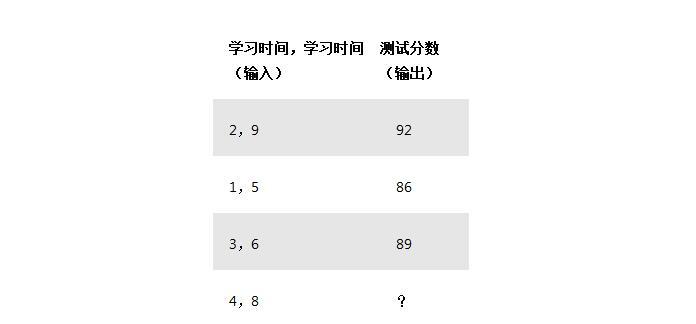
我们的神经网络将模拟一个具有三个输入和一个输出的隐藏层。在网络中,我们将根据我们研究多少小时以及我们前一天睡了多少小时的输入来预测考试成绩。我们的测试分数是输出。以下是我们将在以下方面培训我们的神经网络的示例数据:
正如你可能已经注意到的那样,?在这种情况下代表了我们希望我们的神经网络预测的东西。在这种情况下,我们预测根据他们之前的表现,学习了四个小时并睡了八个小时的人的测试分数。
向前传播
让我们开始编码这个坏男孩!打开一个新的python文件。您需要导入,numpy因为它可以帮助我们进行某些计算。
首先,让我们使用numpy数组导入我们的数据np.array。我们也希望我们的单位标准化,因为我们的输入是以小时为单位的,但是我们的输出是从0到100的测试分数。因此,我们需要通过除以每个变量的最大值来缩放数据。
接下来,让我们定义一个pythonclass并写一个init函数,我们将在其中指定我们的参数,如输入层,隐藏层和输出层。
现在是我们第一次计算的时候了。请记住,我们的突触执行点积或输入和权重的矩阵乘法。请注意,权重是随机生成的,介于0和1之间。
我们网络背后的计算
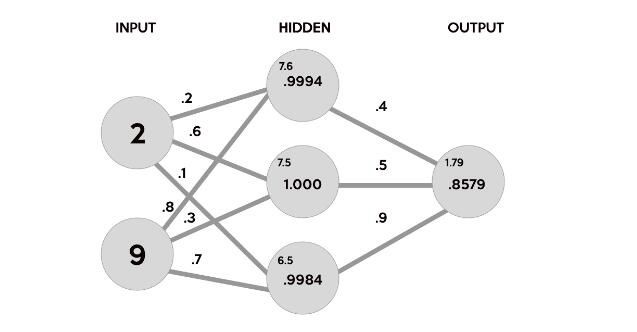
在数据集中,我们的输入数据X是一个3x2的矩阵。我们的输出数据y是一个3x1矩阵。矩阵中的每个元素X需要乘以相应的权重,然后与隐藏层中每个神经元的所有其他结果一起添加。以下是第一个输入数据元素(2小时学习和9小时睡眠)将如何计算网络中的输出:
这张图片分解了我们的神经网络实际上产生输出的过程。首先,将每个突触上随机生成的权重(.2,.6,.1,.8,.3,.7)和相应输入的乘积相加,作为隐层的第一个值。这些总和字体较小,因为它们不是隐藏层的最终值。
(2*.2)+(9*.8)=7.6
(2*.6)+(9*.3)=3.9
(2*.1)+(9*.7)=6.5
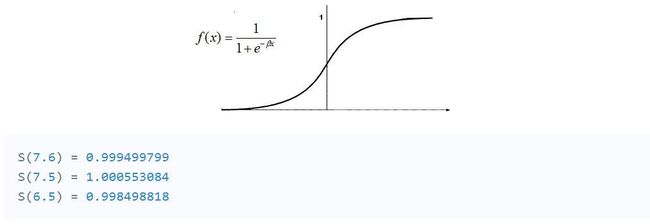
为了获得隐藏层的最终值,我们需要应用激活函数。激活函数的作用是引入非线性。这样做的一个优点是输出从0到1的范围映射,使得将来更容易改变权重。
那里有很多激活功能。在这种情况下,我们将坚持一个更受欢迎的--Sigmoid函数。
现在,我们需要再次使用矩阵乘法和另一组随机权重来计算我们的输出图层值。
(.9994*.4)+(1.000*.5)+(.9984*.9)=1.79832
最后,为了标准化输出,我们再次应用激活函数。
S(1.79832)=.8579443067
而且,你去了!理论上,用这些权重,out神经网络将计算.85为我们的测试分数!但是,我们的目标是.92。我们的结果并不差,但它不是最好的。当我为这个例子选择随机权重时,我们有点幸运。
我们如何训练我们的模型来学习?那么,我们很快就会发现。现在,我们来统计我们的网络编码。
如果您仍然感到困惑,我强烈建议您查看这个带有相同示例的神经网络结构的信息性视频。
实施计算
现在,让我们随机生成我们的权重np.random.randn()。请记住,我们需要两组权重。一个从输入到隐藏层,另一个从隐藏层到输出层。
#weights
self.W1=np.random.randn(self.inputSize,self.hiddenSize)#(3x2)weightmatrixfrominputtohiddenlayer
self.W2=np.random.randn(self.hiddenSize,self.outputSize)#(3x1)weightmatrixfromhiddentooutputlayer
一旦我们有了所有的变量,我们就可以编写我们的forward传播函数了。让我们传入我们的输入,X在这个例子中,我们可以使用变量z来模拟输入层和输出层之间的活动。正如所解释的那样,我们需要获取输入和权重的点积,应用激活函数,取另一个隐藏层的点积和第二组权重,最后应用最终激活函数来接收我们的输出:
defforward(self,X):
#forwardpropagationthroughournetwork
self.z=np.dot(X,self.W1)#dotproductofX(input)andfirstsetof3x2weights
self.z2=self.sigmoid(self.z)#activationfunction
self.z3=np.dot(self.z2,self.W2)#dotproductofhiddenlayer(z2)andsecondsetof3x1weights
o=self.sigmoid(self.z3)#finalactivationfunction
returno
最后,我们需要定义我们的sigmoid函数:
defsigmoid(self,s):
#activationfunction
return1/(1+np.exp(-s))
我们终于得到它了!一个能够产生输出的(未经训练的)神经网络。
importnumpyasnp
#X=(hourssleeping,hoursstudying),y=scoreontest
X=np.array(([2,9],[1,5],[3,6]),dtype=float)
y=np.array(([92],[86],[89]),dtype=float)
#scaleunits
X=X/np.amax(X,axis=0)#maximumofXarray
y=y/100#maxtestscoreis100
classNeural_Network(object):
def__init__(self):
#parameters
self.inputSize=2
self.outputSize=1
self.hiddenSize=3
#weights
self.W1=np.random.randn(self.inputSize,self.hiddenSize)#(3x2)weightmatrixfrominputtohiddenlayer
self.W2=np.random.randn(self.hiddenSize,self.outputSize)#(3x1)weightmatrixfromhiddentooutputlayer
defforward(self,X):
#forwardpropagationthroughournetwork
self.z=np.dot(X,self.W1)#dotproductofX(input)andfirstsetof3x2weights
self.z2=self.sigmoid(self.z)#activationfunction
self.z3=np.dot(self.z2,self.W2)#dotproductofhiddenlayer(z2)andsecondsetof3x1weights
o=self.sigmoid(self.z3)#finalactivationfunction
returno
defsigmoid(self,s):
#activationfunction
return1/(1+np.exp(-s))
NN=Neural_Network()
#definingouroutput
o=NN.forward(X)
print"PredictedOutput:\n"+str(o)
print"ActualOutput:\n"+str(y)
正如您可能已经注意到的那样,我们需要训练我们的网络来计算更准确的结果。
反向传播
由于我们有一组随机的权重,我们需要对它们进行修改,以使我们的输入等于我们数据集的相应输出。这是通过一种称为反向传播的方法完成的。
反向传播通过使用丢失函数来计算网络与目标输出的距离。
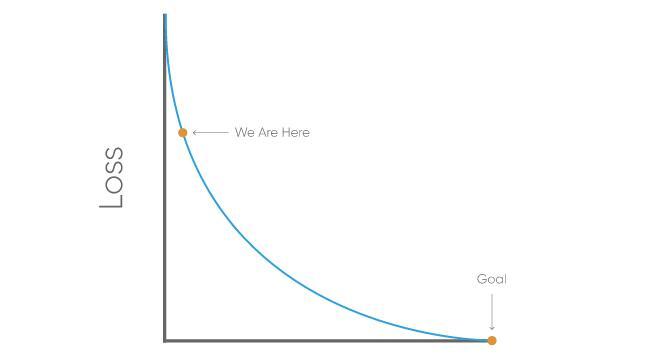
在这个函数中,o是我们的预测输出,并且y是我们的实际输出。既然我们有损失函数,那么我们的目标就是尽可能接近零。这意味着我们将需要接近完全没有损失。当我们正在训练我们的网络时,我们所做的一切就是尽量减少损失。
为了找出改变我们的权重的方向,我们需要找出我们的损失相对于权重的变化率。换句话说,我们需要使用损失函数的导数来理解权重如何影响输入。
在这种情况下,我们将使用偏导数来允许我们考虑另一个变量。
这种方法被称为梯度下降。通过知道哪种方式来改变我们的权重,我们的输出只能得到更准确的结果。
以下是我们将如何计算对权重的增量更改:
通过计算预测输出和实际输出(y)的差值来找出输出层(o)的误差幅度,
将sigmoid激活函数的导数应用于输出图层错误。我们把这个结果称为delta输出和。
使用输出层误差的delta输出总和来计算我们的z2(隐藏)层通过使用我们的第二个权重矩阵执行点积来导致输出误差的程度。我们可以称之为z2错误。
应用我们的sigmoid激活函数的导数(与第2步一样),计算z2层的delta输出和。
通过执行输入层与隐藏(z2)增量输出和的点积来调整第一层的权重。对于第二层,执行隐藏(z2)图层和输出(o)delta输出和的点积。
计算delta输出和然后应用sigmoid函数的导数对于反向传播非常重要。S型的衍生物,也被称为S型素数,将给我们输出和的激活函数的变化率或斜率。
让我们继续Neural_Network通过添加sigmoidPrime(sigmoid的衍生)函数来编写我们的类:
defsigmoidPrime(self,s):
#derivativeofsigmoid
returns*(1-s)
然后,我们要创建我们的backward传播函数,它执行上述四个步骤中指定的所有内容:
defbackward(self,X,y,o):
#backwardpropgatethroughthenetwork
self.o_error=y-o#errorinoutput
self.o_delta=self.o_error*self.sigmoidPrime(o)#applyingderivativeofsigmoidtoerror
self.z2_error=self.o_delta.dot(self.W2.T)#z2error:howmuchourhiddenlayerweightscontributedtooutputerror
self.z2_delta=self.z2_error*self.sigmoidPrime(self.z2)#applyingderivativeofsigmoidtoz2error
self.W1+=X.T.dot(self.z2_delta)#adjustingfirstset(input-->hidden)weights
self.W2+=self.z2.T.dot(self.o_delta)#adjustingsecondset(hidden-->output)weights
我们现在可以通过启动前向传播来定义我们的输出,并通过在函数中调用后向函数来启动它train:
deftrain(self,X,y):
o=self.forward(X)
self.backward(X,y,o)
为了运行网络,我们所要做的就是运行该train功能。当然,我们会想要做到这一点,甚至可能是成千上万次。所以,我们将使用一个for循环。
NN=Neural_Network()
foriinxrange(1000):#trainstheNN1,000times
print"Input:\n"+str(X)
print"ActualOutput:\n"+str(y)
print"PredictedOutput:\n"+str(NN.forward(X))
print"Loss:\n"+str(np.mean(np.square(y-NN.forward(X))))#meansumsquaredloss
print"\n"
NN.train(X,y)
太棒了,我们现在有一个神经网络!如何使用这些训练后的权重来预测我们不知道的测试分数?
预测
为了预测我们的输入测试分数[4,8],我们需要创建一个新的数组来存储这些数据xPredicted。
xPredicted=np.array(([4,8]),dtype=float)
我们还需要按照我们对输入和输出变量所做的那样进行扩展:
xPredicted=xPredicted/np.amax(xPredicted,axis=0)#maximumofxPredicted(ourinputdatafortheprediction)
然后,我们将创建一个打印我们的预测输出的新函数xPredicted。相信与否,我们必须运行的是forward(xPredicted)返回输出!
defpredict(self):
print"Predicteddatabasedontrainedweights:";
print"Input(scaled):\n"+str(xPredicted);
print"Output:\n"+str(self.forward(xPredicted));
要运行这个函数,只需在for循环中调用它。
NN.predict()
如果你想保存你的训练重量,你可以这样做np.savetxt:
defsaveWeights(self):
np.savetxt("w1.txt",self.W1,fmt="%s")
np.savetxt("w2.txt",self.W2,fmt="%s")
最终的结果如下:
importnumpyasnp
#X=(hoursstudying,hourssleeping),y=scoreontest,xPredicted=4hoursstudying&8hourssleeping(inputdataforprediction)
X=np.array(([2,9],[1,5],[3,6]),dtype=float)
y=np.array(([92],[86],[89]),dtype=float)
xPredicted=np.array(([4,8]),dtype=float)
#scaleunits
X=X/np.amax(X,axis=0)#maximumofXarray
xPredicted=xPredicted/np.amax(xPredicted,axis=0)#maximumofxPredicted(ourinputdatafortheprediction)
y=y/100#maxtestscoreis100
classNeural_Network(object):
def__init__(self):
#parameters
self.inputSize=2
self.outputSize=1
self.hiddenSize=3
#weights
self.W1=np.random.randn(self.inputSize,self.hiddenSize)#(3x2)weightmatrixfrominputtohiddenlayer
self.W2=np.random.randn(self.hiddenSize,self.outputSize)#(3x1)weightmatrixfromhiddentooutputlayer
defforward(self,X):
#forwardpropagationthroughournetwork
self.z=np.dot(X,self.W1)#dotproductofX(input)andfirstsetof3x2weights
self.z2=self.sigmoid(self.z)#activationfunction
self.z3=np.dot(self.z2,self.W2)#dotproductofhiddenlayer(z2)andsecondsetof3x1weights
o=self.sigmoid(self.z3)#finalactivationfunction
returno
defsigmoid(self,s):
#activationfunction
return1/(1+np.exp(-s))
defsigmoidPrime(self,s):
#derivativeofsigmoid
returns*(1-s)
defbackward(self,X,y,o):
#backwardpropgatethroughthenetwork
self.o_error=y-o#errorinoutput
self.o_delta=self.o_error*self.sigmoidPrime(o)#applyingderivativeofsigmoidtoerror
self.z2_error=self.o_delta.dot(self.W2.T)#z2error:howmuchourhiddenlayerweightscontributedtooutputerror
self.z2_delta=self.z2_error*self.sigmoidPrime(self.z2)#applyingderivativeofsigmoidtoz2error
self.W1+=X.T.dot(self.z2_delta)#adjustingfirstset(input-->hidden)weights
self.W2+=self.z2.T.dot(self.o_delta)#adjustingsecondset(hidden-->output)weights
deftrain(self,X,y):
o=self.forward(X)
self.backward(X,y,o)
defsaveWeights(self):
np.savetxt("w1.txt",self.W1,fmt="%s")
np.savetxt("w2.txt",self.W2,fmt="%s")
defpredict(self):
print"Predicteddatabasedontrainedweights:";
print"Input(scaled):\n"+str(xPredicted);
print"Output:\n"+str(self.forward(xPredicted));
NN=Neural_Network()
foriinxrange(1000):#trainstheNN1,000times
print"#"+str(i)+"\n"
print"Input(scaled):\n"+str(X)
print"ActualOutput:\n"+str(y)
print"PredictedOutput:\n"+str(NN.forward(X))
print"Loss:\n"+str(np.mean(np.square(y-NN.forward(X))))#meansumsquaredloss
print"\n"
NN.train(X,y)
NN.saveWeights()
NN.predict()
为了看到网络的实际准确程度,我跑了10万次训练,看看能否得到完全正确的输出结果。这就是我得到的:
#99999
Input(scaled):
[[0.666666671.]
[0.333333330.55555556]
[1.0.66666667]]
ActualOutput:
[[0.92]
[0.86]
[0.89]]
PredictedOutput:
[[0.92]
[0.86]
[0.89]]
Loss:
1.94136958194e-18
Predicteddatabasedontrainedweights:
Input(scaled):
[0.51.]
Output:
[0.91882413]
你有它!一个完整的神经网络,可以学习和适应产生准确的输出。虽然我们将我们的输入视为学习和睡眠的小时数,并将我们的输出视为测试分数,但随时可以将这些输入更改为任何您喜欢的内容,并观察网络的适应情况!毕竟,所有的网络都是数字。我们所做的计算虽然很复杂,但都在我们的学习模型中发挥了重要作用。(黑客周刊)