本文首发 http://svtter.cn
最接近的数字
题目
一个K位的数N
$$ (K\leq2000,N\leq10^{20}) $$
找出一个比N大且最接近的数,这个数的每位之和与N相同,用代码实现之。
例如:0050 所求书数字为0104;112 所求数为121;
算法分析 算法思想
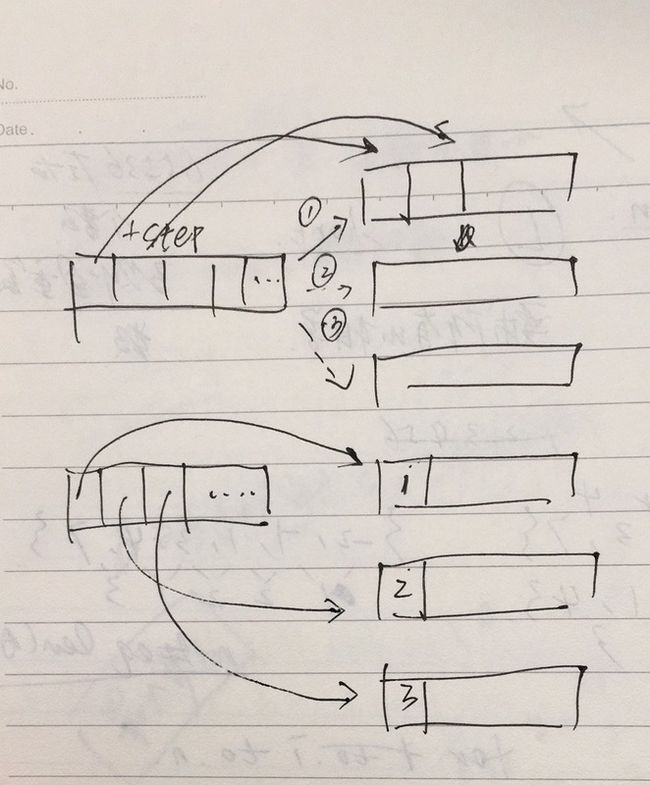
直接暴力求这个数字是不可以的,数字的量级太大,有K位的数字,不可能直接用int,或者float来表示,使用数组来存储。应该分析这个数字,step1,从右边开始的最小位数开始,分解最后一位数字,分解出1来拿给前面的一位。9和0比较特殊,因此从左往右扫描的开始,遇到0就跳过,遇到第一个非0的数字,就把这个数字-1,然后移到最后面去,然后,step2,开始找第一个非9的数字,如果遇到9,就把9放到最后面去,遇到非9,就+1,结束运算。
一个般的例子:
1999000 -> 1990008-> 2000899
要注意一个问题,就是如果是 999000 这种情况,在数字的最开头补1,结果是1000899
几个刁蛮的数据:29399 -> 29489
伪代码
array = get_array() # number to char array
array.reverse()
step1 = true
step2 = false
zero = 0, cnt = 0;
for i : 1 - lengthof(array)
if step1:
if array[i] is 0:
zero ++
else:
array[i] = array[i] - 1
if zero > 0:
array[0] = array[i]
array[i] = 0
step1 = false
step2 = true
else if step2:
if array[i] is 9:
if zero == 0:
array[cnt+1] = array[cnt]
array[cnt] = 9
cnt++
if (i != cnt):
array[i] = array[i-1]
else:
array[cnt + 1] = array[cnt]
array[cnt] = 9
cnt++
array[i] = 0
else:
i = i+1
step2 = false
break
if not step2:
array[lengthof(array)] = 1
array.reverse()
disp(array)分析时间复杂度O
因为reverse操作,2K,加上最后整理最小数到最前面,最坏情况接近K,3K,在循环中的操作看运气,但是最糟糕的情况也只有5K,所以时间复杂度为
$$ O(3K) \approx O(K) $$
源代码
#include
#include
const int MAXN = 3000;
char array[MAXN];
int length_of_number;
void get_array()
{
int i;
char null;
scanf("%d", &length_of_number);
scanf("%c", &null);
for (i = 0; i < length_of_number; i++)
{
scanf("%c", &array[i]);
}
scanf("%c", &null);
}
void reverse()
{
int i ;
char temp;
for (i = 0; i < length_of_number/2; i++)
{
// _swap
temp = array[i];
array[i] = array[length_of_number - 1 - i];
array[length_of_number-1-i] = temp;
}
}
void run()
{
reverse();
int step1 = 1,
step2 = 0,
i = 0,
zero = 0,
cnt = 0;
for (i = 0; i < length_of_number; i++)
{
if (step1)
{
if (array[i] == '0')
{
zero++;
}
else
{
array[i] = array[i] - 1;
if (zero > 0)
{
array[cnt] = array[i];
array[i] = '0';
}
step1 = 0, step2 = 1;
}
}
else if (step2)
{
if (array[i] == '9')
{
if (zero == 0)
{
array[cnt + 1] = array[cnt];
array[cnt] = '9';
cnt++;
if (i != cnt)
{
array[i] = array[i-1];
}
}
else
{
array[cnt + 1] = array[cnt];
array[cnt] = '9';
cnt++;
array[i] = '0';
}
}
else
{
array[i] ++;
step2 = 0;
break;
}
}
}
if (step2)
{
array[length_of_number] = '1';
length_of_number ++;
}
}
void output()
{
int i;
reverse();
for(i = 0; i < length_of_number; i++)
{
printf("%c", array[i]);
}
printf("\n");
}
int main()
{
memset(array, 0, sizeof(array));
freopen("input", "r", stdin);
get_array();
run();
output();
return 0;
} 测试结果
使用python生成测试数据进行测试:
"""
最接近的数字
"""
import random
import os
def test():
"""
sample test
"""
num = random.randint(0, 10000000)
sum_of_num = 0
for i in str(num):
sum_of_num += int(i)
length = len(str(num))
temp_num = num + 1
while(True):
sum_temp = 0
for i in str(temp_num):
sum_temp += int(i)
if sum_temp == sum_of_num:
break
temp_num += 1
with open('input', 'w') as f:
f.write(str(length) + '\n')
f.write(str(num))
res = os.popen('./ex2').read()
if temp_num == int(res):
return [True]
else:
return [False, num, temp_num, int(res)]
all = True
for i in range(1000):
res = test()
if res[0] is False:
all = False
print(res)
if all:
print('Pass testing!')存在错误的情况:
通过:
后期改善优化的地方
reverse 是为了编程方便进行的处理,但是如果数字太大,速度肯定会受影响,这个时候就不要使用reverse了。
用链表来做可以简化代码,减少分析的,更加节省时间
处理移位的时候考虑几个问题
寻找发帖水王
题目
如果“水王”没有了,但有三个发帖很多的ID,发帖的数目都超过了帖子做数的1/4,又如何快速找出他们的ID。
算法分析 算法思想
从0-n扫描ID数组,记录3个数字的个数,如果出现第四个数字,就把三个数字的个数减少1,如果有一个数字的个数减少到0,那么把新来的数字作为原本三个数字之一进行记录。
如此一来,扫描完ID数组之后,剩下记录的3个数字的个数便是需要求的三个数字。
伪代码
array = get_array()
count = empty_set()
for i in array:
if count.full:
if i in count:
count.i.num ++
else:
for j in count:
count.j.num--
else
count.add(i)
disp(count)分析时间复杂度O
数列的大小为N,记录数字的数组大小为3,每次判断记录数组count是否存在0,以及找到已存在的数字++,都会花费3个单位时间,因此其时间复杂度为
$$ O(3n) \approx O(n) $$
源代码
#include
#include
#define MAXN 5000
int idarray[MAXN];
int cur[3]; // 记录当前元素
int pos[3]; // 记录当前元素个数
// 检查是否在数组内,如果不在数组内,添加进入数组
void checkin(int no)
{
int i;
// 检查是否有空位置
for (i = 0; i < 3; i++)
{
if (pos[i] == 0)
{
cur[i] = no;
pos[i] ++;
return;
}
}
// 寻找指定数字++
for (i = 0; i < 3; i++)
{
if (cur[i] == no)
{
pos[i] ++;
return;
}
}
// 没有找到重复数字,全部--
for (i = 0; i < 3; i++)
pos[i] --;
}
// 输出最后结果
void output()
{
printf("%d %d %d\n", cur[0], cur[1], cur[2]);
}
// 主程序
int numberOfArray;
void run()
{
int i;
for (i = 0; i < numberOfArray; i++)
{
checkin(idarray[i]);
}
output();
}
void input()
{
int i;
scanf("%d", &numberOfArray);
for(i = 0; i < numberOfArray; i++)
{
scanf("%d", &idarray[i]);
}
}
int main()
{
freopen("input", "r", stdin);
int groupOfTest;
scanf("%d", &groupOfTest);
while(groupOfTest--)
{
memset(cur, 0, sizeof(cur));
memset(pos, 0, sizeof(pos));
memset(idarray, 0, sizeof(idarray));
input();
puts("Test running...");
run();
}
return 0;
}
测试结果
本测试数据采用Python自动生成。
"""
寻找发帖水王
"""
import random
N = 4000
a, b = (int(N/4), int(N/3))
three_id = random.sample(range(1, 100), 3)
three_id_num = {}
sum_rand = 0
for i in three_id:
temp = random.randint(a, b)
sum_rand += temp
three_id_num[i] = three_id_num.get(i, 0) + temp
id_array = [random.randint(1, 100) for i in range(N-sum_rand)]
for i in three_id:
id_array = id_array + [i for j in range(three_id_num[i])]
random.shuffle(id_array)
print('Most three id:', three_id)
print('Three id num: ', three_id_num)
print('Sum of three_id num: ', sum_rand)
print('---------------')
# print(id_array)
with open('input', 'w') as f:
f.write('1\n')
f.write(str(N) + '\n')
for i in id_array:
f.write(str(i) + ' ')
后期改善优化的地方
对于N比较小的情况可以在内存中进行查找,但是一旦涉及到更大的数据,这个方法可能就没有那么简单了,不能在内部建立数组,需要一部分一部分的从磁盘中读数;
如果需要查找的id数量变多,那么需要的临时保存的数列可能更大;
这个实现没有使用STL中的map,如果使用map,还能进一步使得代码见解易懂,map使用hash来做内部实现,可以使得面对数据量更大的数据的时候,加快查找数据的速度。
山西煤老板
题目
你是山西的一个煤老板,你在矿区开采了有3000吨煤需要运送到市场上去卖,从你的矿区到市场有1000公里,你手里有一列烧煤的火车,这个火车只能装1000吨煤,且能耗比较大——每一公里需要耗一吨煤。请问,作为一个懂编程的煤老板,你会怎么运送才能运最多的煤到集市?
算法分析 算法思想
从动态规划的角度求最优解:
假设起始运送货物量为t,终点路程为s,火车容量为c,可以运抵终点的最多货物量为函数 F(t, s)。
3种基本情况:
(1)t < s:货物量不足以运送到此距离,所以F(t, s) = 0;
(2)s < t < c:火车一次就可以装完货物,所以F(t, s) = t - s;
(3)2s < c 使得火车一次无法运完,但可以采用往返的方式多次运输,这种情况下最有的方式就是减少总共往返的次数,也就是直接运到终点而不在中间卸货,所以
$$ F(t, s) = (t / c - 1) * (c - 2s) + (c - s) $$
可得递归式:
$$ F(t, s) = max\{ F( F(t, i), s - i)\} (1 <= i < s) $$
分析了一下这个方程是有问题的,比如F(1750, 250)会计算出1125;
所以正确的结果应该对t/c进行处理,也就是说,起点剩余的燃料不足运输到终点,直接舍弃。第三阶段的方程式应该是
$$ F(t, s) = (t // c - 1) * (c - 2s) + (c - s) + (t \% c - 2 s), if (t\%c > 2s) $$
伪代码
begin:
if t < s:
f[t][s] = 0
elif s < t < c:
f[t][s] = t - s
elif 2*s < c:
f[t][s] = int((t//c-1)*(c-2*s) + (c-s))
if t % c > 2*s:
f[t][s] += int(t % c-2*s)
else:
pre = -2
for i in range(1, s):
pre = int(max(F(F(t, i), s-i), pre))
f[t][s] = pre
end
disp(f[3000][1000])分析时间复杂度O
时间复杂度为
$$ O(3000*3000) $$
因为每个数字都要计算一遍。
源代码
"""
山西煤老板
"""
c = 1000
f = [[-1 for k in range(4000)] for j in range(4000)]
for j in range(4000):
for k in range(4000):
if j < k:
f[j][k] = 0
count = 1000
cnt = 0
def F(t, s):
"""
dp
"""
global count
global c
global f
# count -= 1
# if count == 0:
# count = int(input())
t = int(t)
s = int(s)
if f[t][s] != -1:
return f[t][s]
if t < s:
f[t][s] = 0
elif s < t < c:
f[t][s] = t - s
elif 2*s < c:
f[t][s] = int((t//c-1)*(c-2*s) + (c-s))
if t % c > 2*s:
f[t][s] += int(t % c-2*s)
else:
pre = -2
for i in range(1, s):
pre = int(max(F(F(t, i), s-i), pre))
f[t][s] = pre
print(t, s, f[t][s])
return f[t][s]
print(F(3000, 500))
测试结果
后期改善优化的地方
去除了一下数据进行加速
保存f减少重复运算值
-
应该有更加简单的方法,类似这种,但是不好解释。
$$ 3y=1000\\ 5x=1000\\ 解得x+y=200+333=533,因此使得最后一辆火车抵达时节省了533吨煤\\ $$
题目
Given a list of words, L, that are all the same length, and a string, S, find the starting position of the substring of S that is concatenation of each word in L exactly once and without intervening characters. This substring will occur exactly once in S.
算法分析 算法思想
使用hashmap来保存word的hash值,来加快查找速度。(旧)
直接用hash函数求字符串的hash值,最后求得结果。
依据公式
$$ hash(w_1) + hash(w_2) = hash(w_2) + hash(w_1) $$
伪代码
hash_word_list = list(map(hash, words))
hash_sum = reduce(lambda x, y: x + y, hash_word_list)
for i in range(len(sentence)):
wl = word_len
wlist = [sentence[i+j*wl:i+j*wl+wl] for j in range(words_len)]
temp_sum = 0
for k in wlist:
temp_sum += hash(k)
if temp_sum == hash_sum:
print(i)
break分析时间复杂度O
就是字符串长度
$$ O(lengthOfS) $$
源代码
#!/usr/bin/env python3
"""
facebook
"""
from functools import reduce
while True:
words = input()
# words = "fooo barr wing ding wing"
words = words.split(' ')
word_len = len(words[0])
words_len = len(words)
hash_word_list = list(map(hash, words))
hash_sum = reduce(lambda x, y: x + y, hash_word_list)
sentence = input()
# sentence = """lingmindraboofooowingdin\
# gbarrwingfooomonkeypoundcakewingdingbarrwingfooowing"""
# print(words, words_len, word_len, sentence)
for i in range(len(sentence)):
wl = word_len
wlist = [sentence[i+j*wl:i+j*wl+wl] for j in range(words_len)]
# print(wlist)
temp_sum = 0
for k in wlist:
temp_sum += hash(k)
if temp_sum == hash_sum:
print(i)
break测试结果
测试数据生成意义不是很大,
后期改善优化的地方
hash尽管在速度上非常优秀,但是在准确度方面,如果出现hash冲突,那么值可能不准确。此时可以利用hashmap来解决这个问题,不过会多出重置hashmap的相关时间。
For n -m - problems
Problemset
Assume we have a sequence that contains N numbers of type long. And we know for sure that among this sequence each number does occur exactly n times except for the one number that occurs exactly m times (0 < m < n). How do we find that number with O(N) operations and O(1) additional memory?
Algorithm
^ is the add operation without carry.
默认one,two都是0, 即任何数字都不存在
数字a第一次来的时候, one标记a存在, two不变
数字a第二次来的时候, one标记a不存在, two标记a存在
数字a第三次来的时候, one不变, two标记a不存在
构造这样一种运算,通过异或将数据保存在one和two里面。
Pseudocode
def solve2(array):
one = 0, two = 0
for i in range(array):
one = (one ^ array[i]) & ~two
two = (two ^ array[i]) & ~one
return one, two
array = input()
_, res = solve2(array)### Source code
#!/usr/bin/env python
def solve(array):
one, two = 0, 0
for i in array:
one = (one ^ i) & ~two
two = (two ^ i) & ~one
return one, two
if __name__ == '__main__':
array = input()
array = array.split(' ')
array = list(map(lambda x: int(x), array))
# print(array)
_, res = solve(array)
print(res)Test
#!/usr/bin/env python3
import random
def test():
"""
测试
"""
array = []
n, m = 3, 2
numberofNum = random.randint(100, 1000)
record = {}
for _ in range(numberofNum):
temp = random.randint(10, 10000)
while temp in record:
temp = random.randint(10, 10000)
record[temp] = 1
for _ in range(3):
array.append(temp)
temp = random.randint(10, 1000)
while temp in record:
temp = random.randint(10, 1000)
array.append(temp)
array.append(temp)
from run import solve
_, res = solve(array)
if res != temp:
print('ERROR')
print(array, temp)
input()
else:
print('Pass: res: ', res, 'temp:', temp)
for i in range(50):
test()
Use python generate data to test.
Discussion and improve
如果n不是3,那么需要构造更多的临时变量。
很长的数组
题目
一个很长很长的short型数组A,将它分成m个长为L的子数组B1,B2,…,Bm,其中每个数组排序后都是递增的等差数列,求最大的L值。
$$ 例如,A = \{-1, 3, 6, 1, 8, 10\} 可以分成B_1 = \{-1, 1, 3\}, B_2 = \{6, 8, 10\},\; L = 3 即为所求。 $$
算法分析
首先进行排序,然后开始分三步走。
统计元素个数 O(n)
-
排序 O(nlog(n))
第一步用来枚举L和m的大小,由题目可知,L * m = 数组的长度。从m为1开始枚举,保证得到的L为最大值。
第二步搜索为深搜,确定当前子数组的起点和初始步长,使用pos记录当前数组选定的元素。
第三步枚举,根据起点给定的初始步长,开始枚举步长,如果枚举的步长可以在数组中找到足够的元素,即数字为L,那么记录这种分法,开始枚举下一个起点。如果枚举的步长和起点无法满足条件,回溯到上一个节点,把上一个节点记录的步长+1再一次搜索。当枚举的起点数达到m,即满足要求输出。
大白话来讲,就是从头开始分原始数组到m个数组中去,排序过后,在前面的每一个节点未被分配的元素,都是子数组起点。如果使用广度优先搜索,即每次都给一个子数组分配一个满足子数组步长要求的数,会导致在最后才发现分配的元素数不满足要求,从而浪费大量时间。
其中,深度优先搜索还有几个剪枝的技巧:
当前步长*(L-1)如果超过了数组的最大元素,可以不继续搜索
-
如果在给定步长的情况下, 下一个数字的大小超过之前的数字+步长,那么可以不必继续搜索。
因为数组已经排好序。
还有其他的剪枝技巧,体现在代码中了。
时间复杂度
n为数组长度,排序的时间为 O(nlogn),枚举m时间为n,枚举step时间为65536【short跨度】,枚举全部元素时间为n,因此算法的时间上界为
$$ O(65536n^2) $$
实际情况下,由于剪枝等操作的存在,应优于这个时间。
伪代码
leng = len(Array)
for m=1 to n:
if n % m != 0:
continue
L = n // m
# deep search
res, record = findArray(L, m)
def findArray(L, m):
group = 0
pos = np.ones(leng)
record = []
record_start = []
while group != m:
step = 0
start = getStart(pos)
res, step = 寻找合适的步长(start, step, pos, record, L)
if res:
找到了计数
while res is False:
没找到弹出栈,往回找
if 弹出栈为空:
不用找了找不到了
return False, None源代码
#!/usr/bin/env python3
# coding: utf-8
"""
arrays
"""
from __future__ import print_function
import numpy as np
array = [-1, 3, 6, 1, 8, 10]
# array = [1, 5, 9, 2, 6, 10]
# array = [1, 2, 4, 5, 8, 9, 13, 14]
# array = [1, 2, 4, 7, 11]
array = sorted(array)
print(array)
leng = len(array)
maxn = array[leng-1]
enable = 1
disable = 0
def findJ(j, step, pos, record, L):
"""
寻找以J为开始,以步长step为开始的数列
"""
class StepError(Exception):
pass
class MaxException(Exception):
pass
if pos[j] == disable:
return False
start = array[j]
pre = start
record_temp = []
# remember zero
try:
for step in range(step, 40000):
# 把第一个数字记录
record_temp.append(j)
pos[j] = disable
pre = start
if start + step * (L - 1) > maxn:
raise MaxException
try:
cnt = 1
if cnt == L:
record.append(record_temp)
return True, step
for k in range(j, leng):
if pos[k] == disable:
continue
elif pos[k] == enable and array[k] == pre + step:
record_temp.append(k)
pre = array[k]
cnt += 1
pos[k] = disable
elif pos[k] == enable and array[k] > pre + step:
raise StepError
if cnt == L:
record.append(record_temp)
return True, step
except StepError:
# 重置标记
for r in record_temp:
pos[r] = enable
record_temp = []
except MaxException:
# 没有合适的step
return False, None
def findArray(L, m):
"""
寻找数组
"""
pos = np.ones(leng)
record = []
record_start = []
group = 0
while group != m:
start = 0
while pos[start] == disable:
start += 1
step = 0
res, step = findJ(start, step, pos, record, L)
if res:
group += 1
record_start.append((start, step))
while res is False:
try:
start, step = record_start.pop()
for r in record.pop():
pos[r] = enable
group -= 1
res, step = findJ(start, step+1, pos, record, L)
except IndexError:
return False, None
return True, record
def divideArray():
"""
分离数组
m 是分离的数组的个数
L 是分离的数组的长度
"""
for m in range(1, leng+1):
if leng % m != 0:
continue
L = leng // m
res, record = findArray(L, m)
def trans(x):
return array[x]
if res:
print('lenth: ', L)
for r in record:
temp = map(trans, r)
print(list(temp))
return
print('No result.')
if __name__ == '__main__':
divideArray()测试
测试样例生成结果未必准确,找了部分的测试样例,可以通过修改代码中array来提现。
讨论
在记录了起点和步长,应该可以利用这两点推出当前使用了哪些元素,如果空间大小不够使用,可以不适用record记录,如果下一层不满足条件回溯的时候,可以利用起点和步长回推已经使用的元素。